poj1177

(题目链接)

1.扫描线

题意

　　求矩形周长并。

Solution

　　转自

　　先看图：

　　

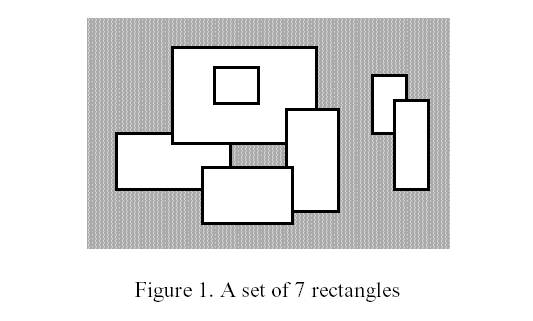
　　为了解决这个问题 我们先把一坨一坨的矩形 进行矩形切割：

　　

　　

　　

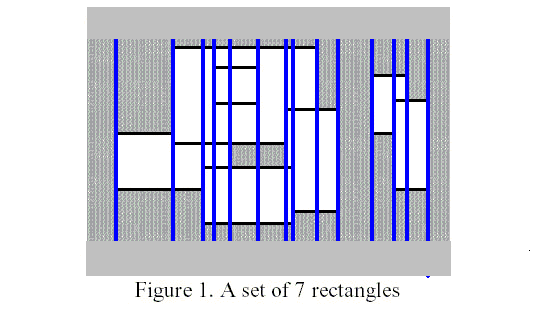
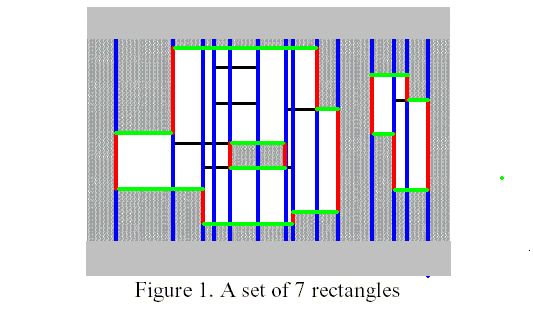
　　我们考虑周长由哪些部分构成

　　其中，红线是需要统计入周长的竖边，绿线是需要统计入周长的横边

　　我们称两条蓝线之间的部分为统计区间

　　我们需要依次统计从左到右的统计区间内的需要计数的矩形边，累加

　　形象地讲，就是用一根扫描线，从左到右依次扫描

　　具体实现就是依次遍历那些蓝线然后，累加每个区间的统计结果

　　我们任取2个统计区间进行详细讨论，放大前2个统计区间部分

　　

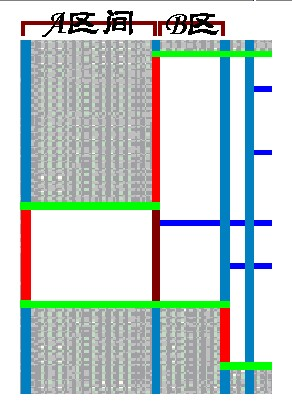
　　考虑为什么同样是矩形边，红边需要统计而棕色的边不需要统计

　　我们发现深红色的边包含在第一个矩形内部，也就是夹在第一个矩形两条红边之间

　　继续分析，我们可以知道，横边也是这样

　　深蓝色边加在统计区间内的两条绿色边之间，属于矩形内部，不需要统计

　　那么，如何判定是否是红边或绿边呢？

　　我们在扫描线上投下当前经过扫描线矩形的投影

　　

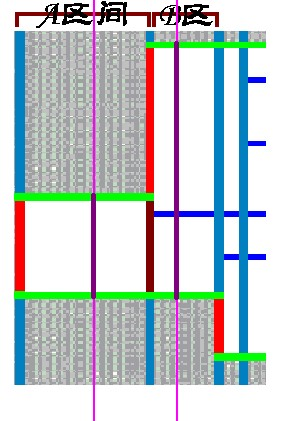
　　红边必然造成投影的变化，绿边必然在投影上线段的端点处

　　没有造成投影变化的竖边，肯定在投影内部，也就是在还未扫描完的矩形内部

　　

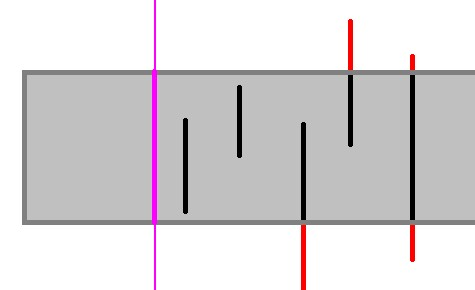
　　 不在投影线段段端点处的横边 也会夹在在投影线段端点处的两个矩形边内

 　　

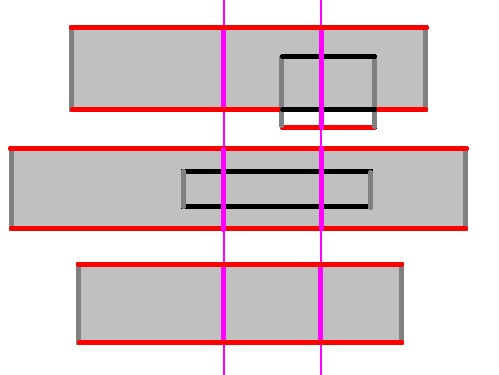
　　于是，我们将绿边的长度=统计区间宽*投影连续段数*2

　　再与红边的长度=与上一个区间投影的差求和，即得到当前区间的统计值，再累加即可

　　考虑怎么统计答案，我们采用线段树：

　　先将一个矩形一分为二，分别记录下左竖边，右竖边，差分。将竖边按照左端点排序，扫描线从左到右扫描，依次将竖边所在的区间加入线段树，统计答案。

　　用线段树记录下扫描线上的投影的情况

　　当扫描线碰到举行左边的时候就插入这个线段，碰到矩形右边就删除这个线段（差分）

　　我们还要重新规划在线段树上的域：覆盖次数cov[]，连续段数num[]，长度len[](即被覆盖的总长度)

　　这几个域需要我们实时维护，更需增加维护的域ls[]，rs[]表示左右端点是否被覆盖

　　于是问题至此就差不多解决了，注意我们线段树上记录的是区间而不是端点，这样更方便我们统计答案。

细节

　　左右下标。

2.线段树

1. 离散化：下面的代码是对y进行离散，根据y排序去重后建树
2. 将竖边加入数组，记录入边和出边，根据x排序
3. 通过二分查找找到边纵坐标所在下标
4. 处理后计算周长

代码（线段树）

#include <iostream>
#include <string>
#include <cstdlib>
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAX=10010;
struct node
{
    int a,b,sum,len,f,num;
    bool l,r;
    node* x,*y;
}*d,ld[MAX*4];
struct Node
{
    int s,t,x,f;
}e[MAX];
int dx[MAX];
int t=0,n,l=0,ls=0,top=1;
bool cmp(const Node &a,const Node &b)
{
    return a.x<b.x||(a.x==b.x&&a.s<b.s);
}
void build(node *&d,int a,int b)
{
    int mid=(a+b)>>1;
    t++;d=&ld[t];
    d->a=a;d->b=b;d->f=0;
    d->sum=0;d->num=0;d->len=dx[b]-dx[a];
    d->l=false;d->r=false;
    if(b-a==1)return;
    build(d->x,a,mid);build(d->y,mid,b);
}
void get_len(node *&d)
{
    if(d->f>0)
    {
        d->sum=d->len;
        return;
    }
    if(d->b-d->a>1)
    {
        d->sum=d->x->sum+d->y->sum;
        return;
    }
    d->sum=0;
}
void get_num(node *&d)
{
    if(d->f>0)
    {
        d->l=true;d->r=true;d->num=1;
    }
    else if(d->b-d->a>1)
    {
        d->l=d->x->l;d->r=d->y->r;
        d->num=d->x->num+d->y->num-d->x->r*d->y->l;
    }
    else
    {
        d->l=false;d->r=false;d->num=0;
    }
}
void change(node *&d,int a,int b,int f)
{
    int mid=(d->a+d->b)>>1;
    if(d->a==a&&d->b==b)
    {
        d->f+=f;
        get_len(d);
        get_num(d);
        return;
    }
    if(b<=mid)
    {
        change(d->x,a,b,f);
    }
    else if(a>=mid)
    {
        change(d->y,a,b,f);
    }
    else
    {
        change(d->x,a,mid,f);
        change(d->y,mid,b,f);
    }
    get_len(d);
    get_num(d);
}
int main()
{
    scanf("%d",&n);
    for(int i=1,a,b,c,d;i<=n;i++)
    {
        scanf("%d%d%d%d",&a,&b,&c,&d);
        dx[i*2-1]=b;dx[i*2]=d;
        e[i*2].s=b;e[i*2-1].s=b;
        e[i*2].t=d;e[i*2-1].t=d;
        e[i*2].x=c;e[i*2-1].x=a;
        e[i*2].f=-1;e[i*2-1].f=1;
    }
    sort(dx+1,dx+n*2+1);
    sort(e+1,e+n*2+1,cmp);
    for(int i=2;i<=2*n;i++)
    {
        if(dx[i]!=dx[top])
        {
            top++;dx[top]=dx[i];
        }
    }
    build(d,1,top);
    for(int i=1,a,b;i<2*n;i++)
    {
        a=lower_bound(dx+1,dx+top+1,e[i].s)-dx;
        b=lower_bound(dx+1,dx+top+1,e[i].t)-dx;
        change(d,a,b,e[i].f);
        l=l+abs(d->sum-ls);
        l=l+d->num*2*(e[i+1].x-e[i].x);
        ls=d->sum;
    }
    int a,b;
    a=lower_bound(dx+1,dx+top+1,e[2*n].s)-dx;
    b=lower_bound(dx+1,dx+top+1,e[2*n].t)-dx;
    change(d,a,b,e[2*n].f);
    l=l+abs(d->sum-ls);
    printf("%d",l);
    return 0;
}

代码（扫描线）

#include<algorithm>

#include<iostream>

#include<cstdlib>

#include<cstring>

#include<cstdio>

#include<cmath>

#define LL long long

#define inf 2147483640

#define Pi acos(-1.0)

#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);

using namespace std;

   

const int maxn=20010;

struct tree {int l,r,len,ls,rs,num,cov;}tr[maxn<<2];

struct data {int x,l,r,val;}a[maxn];

int n;

  

void build(int k,int s,int t) {

    tr[k].l=s;tr[k].r=t;

    if (s==t) return;

    int mid=(s+t)>>1;

    build(k<<1,s,mid);

    build(k<<1|1,mid+1,t);

}

void merge(int k) {

    int l=tr[k].l,r=tr[k].r;

    if (tr[k].cov) {

        tr[k].ls=tr[k].rs=1;

        tr[k].num=2;

        tr[k].len=r-l+1;

    }

    else if (l==r) tr[k].ls=tr[k].rs=tr[k].len=tr[k].num=0;

    else {

        tr[k].num=tr[k<<1].num+tr[k<<1|1].num;

        tr[k].len=tr[k<<1].len+tr[k<<1|1].len;

        tr[k].ls=tr[k<<1].ls;tr[k].rs=tr[k<<1|1].rs;

        if (tr[k<<1].rs && tr[k<<1|1].ls) tr[k].num-=2;

    }

}

void update(int k,int s,int t,int val) {

    int l=tr[k].l,r=tr[k].r,mid=(l+r)>>1;

    if (s<=l && t>=r) {tr[k].cov+=val;merge(k);return;}

    if (s<=mid) update(k<<1,s,t,val);

    if (t>mid) update(k<<1|1,s,t,val);

    merge(k);

}

bool cmpx(data a,data b) {

    return a.x<b.x;

}

int main() {

    scanf("%d",&n);

    int m=0,l=inf,r=-inf;

    for (int x1,x2,y1,y2,i=1;i<=n;i++) {

        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);

        l=min(l,y1);r=max(r,y2);

        a[++m]=(data){x1,y1,y2,1};a[++m]=(data){x2,y1,y2,-1};

    }

    n=m;

    build(1,l,r-1);

    sort(a+1,a+1+n,cmpx);

    int ans=0;

    for (int i=1;i<=n;i++) {

        int tmp=tr[1].len;

        if (i!=1) ans+=tr[1].num*(a[i].x-a[i-1].x);

        update(1,a[i].l,a[i].r-1,a[i].val);

        ans+=abs(tr[1].len-tmp);

    }

    printf("%d",ans);

    return 0;

}