P4498 - 疯狂赛车 题解
感觉挺可做的一个题,为什么人人爆零笑开颜呢?想必是因为部分分完全不简单于正解罢。
遇到这类「无限个点的平面上的最短路」,一般的方法是通过分析性质排除掉大部分不可能出现在最优路径上的点,留下有限个「关键点」,然后至少能有多项式复杂度做法了。
考虑一条最优路径,一定是一条折线。这些折线中相邻的两条一定不都是沙地上的,因为这样直接走前者的左端到后者的右端的直线会更短。如果出现两条相邻的线段都是在赛道上的,我们也可以给两者之间安排上一条长度为 \(0\) 的沙地边,这样就规范了最优路径的形态:取赛道上的所有线段的一个子集的一个排列 \(p_{1\sim m}\)(\(p_i\) 是线段),并选取 \(p_i\) 的某条非空子线段 \(q_i\)(满足 \(a_{q_1}=\pmb 0\),\(b_{q_m}\) 为目的地),最终就是按照 \(q\) 的顺序走,\(b_{q_i}\to a_{q_{i+1}}\) 直接走沙地。
- 为什么选的 \(p_i\) 没有重复?显然,一条赛道上的两个点的最短路就是直线距离,如果出现两次 \(p_i\) 上的点,显然直接缩成一次走就好了。
- 为什么 \(q_i\) 一定非空(\(a_{q_i}\neq b_{q_i}\))呢?不然的话,\(b_{q_{i-1}}\to a_{q_{i+1}}\) 直接走直线就行了,至于 \(i=1/n\) 问题不大。
但现在关键点还不是有限的,还是取遍了赛道上的所有点。考虑 \(q_i\to q_{i+1}\),固定 \(b_{q_i}\),\(a_{q_{i+1}}\) 一定是满足「\(P\) 在 \(p_{i+1}\) 上且 \(\dfrac{1}{v_s}Pb_{q_i}+\dfrac1{v_f}Pb_{q_{i+1}}\)」的 \(P\)。现在来考虑一下这个 \(P\) 怎么求。
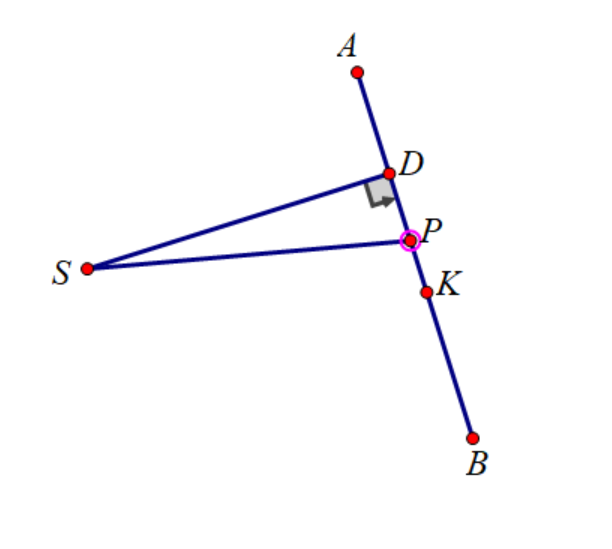
如图,作 \(S\) 到 \(AB\) 的垂线,先假装垂足 \(D\) 在 \(AB\) 上。那么 \(P\) 不可能在 \(AD\) 上,因为越往上去 \(PS\) 和 \(PK\) 都增大。同理,也不可能在 \(KB\) 上,只能在 \(DK\) 上。设 \(DK=L\),现在只要求出 \(DP=x\)。设 \(SD=d\),那么 \(PS=\sqrt{d^2+x^2}\),\(PK=L-x\)。要最小化 \(kPK+PS\)(其中 \(k\in(0,1)\),在原问题中 \(k=\dfrac{v_s}{v_f}\))。
求 \(f(x)=kL-kx+\sqrt{d^2+x^2}\) 的最小值,求导得 \(f'(x)=-k+\dfrac{x}{\sqrt{d^2+x^2}}=0\),解得 \(x=\dfrac{kd}{\sqrt{1-k^2}}\)。但是有可能 \(x>L\),那就只能取 \(x=L\)。再者,有可能 \(D\) 不在 \(AB\) 上,那就再把 \(A,B\) chk 一下。总之就是,要么是 \(x=\dfrac{kd}{\sqrt{1-k^2}}\),要么把 \(K,A,B\) 都 chk 一下就好了。我们惊奇的发现,这个解竟然与 \(L\)(也就是 \(K\) 的位置)无关,只与 \(AB,S\) 有关!(虽然 chk \(K\) 的时候还是要考虑一下的)
回到原问题。也就是固定 \(b_{q_i}\) 后,\(a_{q_{i+1}}\) 只可能是一个由 \(b_{q_i}\) 与 \(p_{i+1}\) 共同决定的关键点,也可能是 \(p_{i+1}\) 的端点或者 \(b_{q_{i+1}}\) 本身。但到目前仍然做不了。考虑再移动 \(b_{q_i}\)。
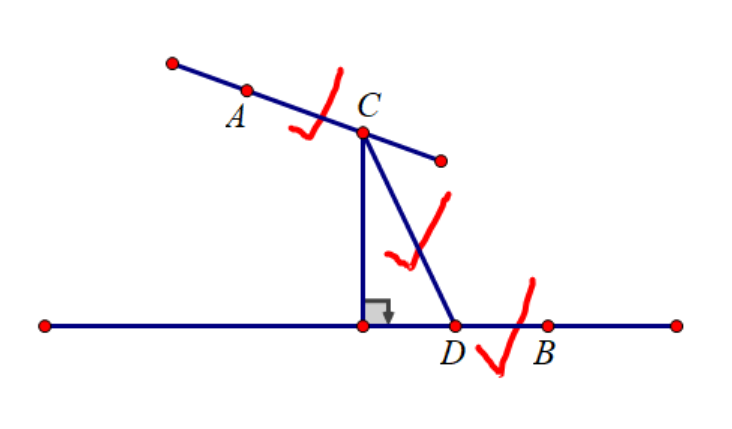
其中 \(A,B,C,D\) 分别表示 \(a_{q_i},b_{q_{i+1}},b_{q_i},a_{q_{i+1}}\)(满足 \(D\) 是 \(A\) 到水平线段 \(p_{i+1}\) 的 \(P\) 点,其与 \(B\) 的具体位置无关,只与 \(B\) 在垂线的哪一侧有关)。当 \(C\) 在 \(A\) 的固定一侧,\(D\) 在 \(B\) 的固定一侧时,考察式子 \(x=\dfrac{kd}{\sqrt{1-k^2}}\),由于 \(k\) 是个常数,所以这是个关于 \(d\) 的线性函数!接下来不难知道,\(AC,CD,DB\) 都是关于 \(d\) 的线性函数,也就是 \(a_{q_i}\to b_{q_{i+1}}\) 的总时间是关于 \(d\) 的线性函数。而线性函数的极值总是在无穷处取到,对应到线段上就是往某一边一直移动直到撞到了端点或 \(A,B\) 停下来,此时取到了极值。而我们之前分析过,\(A\neq C,B\neq D\),所以只可能是 \(C,D\) 中至少一个取到了线段端点!
通过上述分析,我们得到重要结论:对 \(i\in[1,n)\),\(b_{q_i},a_{q_{i+1}}\) 中必有一个是题目中给出的点,而另一个自然就是该点到另一条线段的「之前求出的 \(P\)」(或端点)。设 \(f_{0/1}(x,s)\) 为点 \(x\) 到线段 \(s\) 的 \(P\) 点,\(0/1\) 表示取垂线哪一侧。那么我们只需要保留所有赛道端点和所有 \(f_{?}(x,s)\)(其中 \(x\) 是赛道端点,\(s\) 是赛道线段),点数 \(\mathrm O\!\left(n^2\right)\)。边呢?显然每个 \(f_?(x,s)\) 对应 \(\mathrm O(1)\) 条边,这部分是平方的;以及每对赛道端点的距离,平方;还要将坐落在某条固定的赛道线段上的所有点之间两两连边,这部分看起来是三方,但排个序连相邻点即可做到平方。最后跑 dijkstra,总复杂度 \(\mathrm O\!\left(n^2\log n\right)\)。
code(省略了计算几何板子)
constexpr int N = 1010, M = N + 2 * N * N;
int n;
db vf, vs, k;
point a[N];
int m;
vector<tuple<int, db>> nei[M];
db dis[M];
void dijkstra() {
static bool vis[M];
REP(i, 0, m) dis[i] = 1e14;
using tdi = tuple<db, int>;
priority_queue<tdi, vector<tdi>, greater<tdi>> q; q.push(mt(dis[0] = 0, 0));
while(SZ(q)) {
int x = Y(q.top()); q.pop();
if(vis[x]) continue; vis[x] = true;
for(auto p : nei[x]) {
int y = X(p); db len = Y(p);
if(dis[x] + len < dis[y]) dis[y] = dis[x] + len, q.push(mt(dis[y], y));
}
}
}
void mian() {
n = read();
scanf("%Lf%Lf", &vf, &vs), k = vs / vf;
REP(i, 1, n) a[i].x = read(), a[i].y = read();
REP(i, 0, n) REP(j, 0, n) if(i != j) {
nei[i].pb(j, ~(a[i] - a[j]) / (abs(i - j) == 1 ? vf : vs));
}
m = n;
REP(i, 1, n) {
segment seg(a[i - 1], a[i]);
vector<tuple<db, int>> keys = {mt(0, i - 1), mt(~(a[i - 1] - a[i]), i)};
REP(j, 0, n) if(j != i - 1 && j != i) {
auto rotate = [&](point p) { return point(-p.y, p.x); };
point p = a[j];
point perp = inter(line(p, rotate(a[i - 1] - a[i])), line(a[i], a[i - 1] - a[i]));
db d = ~(perp - p);
db x = k * d / sqrt(1 - sq(k));
point unt = (a[i - 1] - a[i]).unit();
for(int dir : {1, -1}) {
point key = perp + dir * x * unt;
if(!seg.on(key)) continue;
keys.pb(~(a[i - 1] - key), ++m);
db t = ~(key - p) / vs;
nei[j].pb(m, t), nei[m].pb(j, t);
}
}
sort(ALL(keys));
REP(j, 0, SZ(keys) - 2) {
db t = (X(keys[j + 1]) - X(keys[j])) / vf;
nei[Y(keys[j])].pb(Y(keys[j + 1]), t), nei[Y(keys[j + 1])].pb(Y(keys[j]), t);
}
}
dijkstra();
printf("%.6Lf\n", dis[n]);
}

