（一）：细说贝叶斯滤波：Bayes filters

认知计算，还要从贝叶斯滤波的基本思想讲起，本文主要是对《Probabilistic Robotics》中贝叶斯滤波器部分的详细讲解。

这一部分，我们先回顾贝叶斯公式的数学基础，然后再来介绍贝叶斯滤波器。

(一). 概率基础回顾

我们先来回顾一下概率论里的基本知识：

1. $ X $: 表示一个随机变量，如果它有有限个可能的取值$ \{x_1, x_2, \cdots, x_n \} $.

2. $ p(X=x_i) $:表示变量$ X $的值为 $ x_i $的概率。

3. $ p(\cdot) $:称为概率质量函数(probability mass function).

例如：一个家里有3个房间，机器人在各个房间的概率为 $ p(room)=\{0.1, 0.3, 0.6\} $.

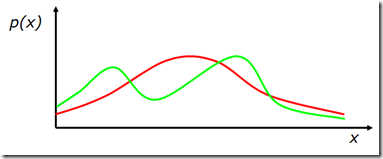
4. 如果$ X $在连续空间取值，$ p(x) $称为概率密度函数(probability density function)，

$$p (x \in (a,b)) = \int\limits_a^b {p(x)dx} $$

图1. 概率密度函数曲线示例

5. 联合概率：$ p(X=x ~~\textrm{and} ~~Y=y) = p(x,y) $，称为联合概率密度分布。如果$X$和$Y$是相互独立的随机变量，$p(x,y)=p(x)p(y)$。

6. 条件概率：$ p(X=x|Y=y) $ 是在已知$Y=y$的条件下，计算$X=x$的概率。

$$ p(x|y)=p(x,y)/p(y)$$

$$ p(x,y)=p(x|y)p(y)=p(y|x)p(x)$$

如果$x$和$y$相互独立，则：

$$ p(x|y)=p(x)$$

7. 全概率公式：

离散情况下:

$$p(x) = \sum\limits_y {p(x,y)}=\sum\limits_y {p(x|y)p(y)} $$

连续情况下：

$$p(x) = \int {p(x,y)\;dy} = \int {p(x|y)p(y)\;dy} $$

(二). 贝叶斯公式

2.1 贝叶斯公式

基于条件概率公式和全概率公式，我们可以导出贝叶斯公式：

$$\begin{array}{c}
P(x,y) = P(x|y)P(y) = P(y|x)P(x)\\
\Rightarrow \\
P(x\,\left| {\,y} \right.) = \frac{{P(y|x)\,\,P(x)}}{{P(y)}} = \frac{{{\textrm{causal knowledge}} \cdot {\textrm{prior knowledge}}}}{{{\textrm{prior knowledge}}}}
\end{array}$$

这里面$x$一般是某种状态；$y$一般是代表某种观测。
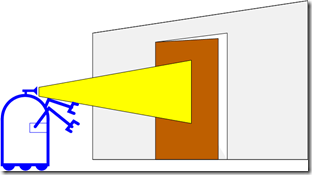
我们称${P(y|x)}$为causal knowledge，意即由$x$的已知情况，就可以推算$y$发生的概率，例如在图2的例子中，已知如果门开着，则$z=0.5m$的概率为0.6；如果门关着，则$z=0.5m$的的概率为0.3。
我们称${P(x)}$为prior knowledge，是对$x$的概率的先验知识。例如在图2的例子中，可设门开或关的概率各占$50\%$.
${P(x|y)}$是基于观测对状态的诊断或推断。贝叶斯公式的本质就是利用causal knowledge和prior knowledge来进行状态推断或推理。

例1: Dog face ：

在图2所示的例子中，机器人根据观测的到门的距离，估算门开或关的概率，若测量到门的距离为$z=0.5m$，则可用条件概率描述门开着的概率：

$$P(\textrm{open}|z=0.6) = ?$$

图 2.机器人根据观测计算门开或关的概率

$$\begin{array}{l}
P(open|z=0.5) = {\textstyle{{P(z|open)P(open)} \over {P(z)}}}{~~~~\rm{ <--贝叶斯公式 }}\\
= \frac{{P(z|open)P(open)}}{{P(z|open)p(open) + P(z|\neg open)p(\neg open)}}{~~~~\rm{ <--全概率公式 }}\\
= \frac{{0.6 \cdot 0.5}}{{0.6 \cdot 0.5 + 0.3 \cdot 0.5}} = 2/3
\end{array}$$

2.2 贝叶斯公式的计算

可以看到贝叶斯公式的分母项${P(y)}$，同${P(x|y)}$无关，所以可以把它作为归一化系数看待：

$$\begin{array}{l}
P(x\,\left| {\,y} \right.) = \frac{{P(y|x)\,\,P(x)}}{{P(y)}} = \eta \;P(y|x)\,P(x)\\
\eta = P{(y)^{ - 1}} = \frac{1}{{\sum\limits_x {P(y|x)} P(x)}}
\end{array}$$

所以基于causal knowledge和prior knowledge进行条件概率计算的过程如下：

Algorithm:

$\begin{array}{l}
\forall x:{\rm{au}}{{\rm{x}}_{x|y}} = P(y|x)\,\,P(x)\\
\eta = \frac{1}{{\sum\limits_x {{\rm{au}}{{\rm{x}}_{x|y}}} }}\\
\forall x:P(x|y) = \eta \;{\rm{au}}{{\rm{x}}_{x|y}}
\end{array}$

2.3 贝叶斯公式中融合多种观测

在很多应用问题中，我们会用多种观测信息对一个状态进行猜测和推理，贝叶斯公式中是如何融合多种观测的呢？

我们简单推导一下：

$$\begin{array}{l}
P(x|y,z){\rm{ = }}\frac{{P(x,y,z)}}{{P(y,z)}}\\
= \frac{{P(y|x,z)p(x,z)}}{{P(y,z)}}\\
= \frac{{P(y|x,z)p(x|z)p(z)}}{{P(y|z)p(z)}}\\
= \frac{{P(y|x,z)p(x|z)}}{{P(y|z)}}
\end{array}$$

所以有：

$$P(x|y,z) = \frac{{P(y|x,z)\,\,P(x|z)}}{{P(y|z)}}$$

2.4 贝叶斯递推公式

由此，我们来推导贝叶斯滤波的递推公式：

$P(x|z_1, \ldots ,z_n) =?$

我们把$z_n$看做$y$，把$z_1, \ldots, z_{n-1}$看做$z$，代入上面的公式：

$$P(x|z_1, \ldots ,z_n) = \frac{{P(z_n|x,z_1, \ldots ,z_{n – 1})\;P(x|z1, \ldots ,z_{n – 1})}}{{P(z_n|z_1, \ldots ,z_{n – 1})}}$$

再由Markov属性，在$x$已知的情况下，$z_n$同$\{z_1, \ldots ,z_{n – 1}\}$无关，所以：

$$\begin{array}{c}
P(x|z_1, \ldots ,z_n) = \frac{{P(z_n|x,z_1, \ldots ,z_{n – 1})\;P(x|z1, \ldots ,z_{n – 1})}}{{P(z_n|z_1, \ldots ,z_{n – 1})}}\\
=\frac{{P(z_n|x)\;P(x|z1, \ldots ,z_{n – 1})}}{{P(z_n|z_1, \ldots ,z_{n – 1})}}
\end{array}$$

从而我们得到贝叶斯的递推公式：

$$\begin{array}{*{20}{l}}
{P(x|{z_1}, \ldots ,{z_n})}&{ = \frac{{P({z_n}|x)\;P(x|{z_1}, \ldots ,{z_{n{\rm{ - }}1}})}}{{P({z_n}|{z_1}, \ldots ,{z_{n - 1}})}}}\\
{}&{ = {\eta _n}\;P({z_n}|x)\;P(x|{z_1}, \ldots ,{z_{n - 1}})}\\
{}&\begin{array}{l}
= {\eta _n}\;P({z_n}|x)\;{\eta _{n - 1}}P({z_{n - 1}}|x)P(x|{z_1}, \ldots ,{z_{n - 2}})\\
= {\eta _1} \cdots {\eta _n}\;\prod\limits_{i = 1...n} {P({z_i}|x)} \;P(x)
\end{array}
\end{array}$$

例2： Dog face 在例1的基础上，如果机器人第二次测量到门的距离仍然为0.5米，计算门开着的概率。

$\begin{array}{lllll}
P(open|{z_2},{z_1}) & = \;\;\frac{{P({z_2}|open)\;P(open|{z_1})}}{{P({z_2}|open)\;P(open|{z_1}) + P({z_2}|\neg open)\;P(\neg open|{z_1})}}\\
& = \;\;\frac{{0.6 \cdot \frac{2}{3}}}{{0.6 \cdot \frac{2}{3} + 0.3 \cdot \frac{1}{3}}}\;\; = \;\;\frac{{0.4}}{{0.5}}\;\; = \;\;0.8
\end{array}$

所以，第二次z=0.5m的观测增大了对门开着的概率的置信程度。

(三). 如何融入动作？

在实际问题中，对象总是处在一个动态变化的环境中，例如：

机器人自身的动作影响了环境状态
其它对象，比如人的动作影响了环境状态
或者就是简单的环境状态随着时间发生了变化。

如何在Bayes模型中来描述动作的影响呢?

首先，动作所带来的影响也总是具有不确定性的
其次，相比于观测，动作一般会使得对象的状态更为模糊（或更不确定）。

我们用$u$来描述动作，在$x'$状态下，执行了动作$u$之后，对象状态改变为$x$的概率表述为：

$$P(x|u,x’)$$

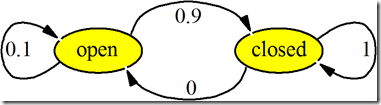
动作对状态的影响一般由状态转移模型来描述。如图3所示，表示了“关门”这个动作对状态影响的转移模型。这个状态转移模型表示：关门这个动作有0.1的失败概率，所以当门是open状态时，执行“关门”动作，门有0.9的概率转为closed状态，有0.1的概率保持在open状态。门是closed的状态下，执行“关门”动作，门仍然是关着的。

图3. “关门”动作的状态转移模型

执行某一动作后，计算动作后的状态概率，需要考虑动作之前的各种状态情况，把所有情况用全概率公式计算：

连续情况下：

$$P(x|u) = \int {P(x|u,x')P(x')dx'} $$

离散情况下：

$$P(x|u) = \sum {P(x|u,x')P(x')} $$

例3： Dog face 在例2的基础上，如果按照图3所示的状态转移关系，机器人执行了一次关门动作，计算动作后门开着的概率？

$$\begin{array}{lllll}
P(open|u) & = \sum {P(open|u,x')P(x')} \\
& \,\, = P(open|u,open)P(open)\\
& \quad + P(open|u,closed)P(closed)\\
& {\kern 1pt} \; = \frac{1}{{10}} * 0.8 + \frac{0}{1} * 0.2 = 0.08\\
\end{array}$$

$$\begin{array}{lllll}
P(closed|u) & = \sum {P(closed|u,x')P(x')} \\
& \,\, = P(closed|u,open)P(open)\\
& \quad + P(closed|u,closed)P(closed)\\
& {\kern 1pt} \; = \frac{9}{{10}} * 0.8 + \frac{1}{1} * 0.2 = 0.92
\end{array}$$

所以，执行一次关门动作后，门开着的概率变为了0.08.

(四). 贝叶斯滤波算法

4.1 算法设定

由上述推导和示例，我们可以给出贝叶斯滤波的算法，算法的输入输出设定如下。

系统输入
1. 1到$t$时刻的状态观测和动作：${d_t} = \{ {u_1},{z_1}\; \ldots ,{u_t},{z_t}\} $
2. 观测模型：$P(z|x)$
3. 动作的状态转移模型：$P(x|u,x’)$
4. 系统状态的先验概率分布$P(x)$.
期望输出
1. 计算状态的后延概率，称为状态的置信概率：$Bel({x_t}) = P({x_t}|{u_1},{z_1}\; \ldots ,{u_t},{z_t})$

4.2 算法基本假设

贝叶斯滤波的基本假设：

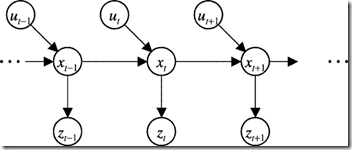
1. Markov性假设: $t$时刻的状态由$t-1$时刻的状态和$t$时刻的动作决定。$t$时刻的观测仅同$t$时刻的状态相关，如图4所示：

图4. Markov模型

$p({z_t}|{x_{0:t}},{z_{1:t}},{u_{1:t}})\,\,\, = \,\,\,p({z_t}|{x_t})$
$p({x_t}|{x_{1:t - 1}},{z_{1:t}},{u_{1:t}})\,\,\, = \,\,\,p({x_t}|{x_{t - 1}},{u_t})$

2. 静态环境，即对象周边的环境假设是不变的

3. 观测噪声、模型噪声等是相互独立的

4.3 Bayes滤波算法

基于上述设定和假设，我们给出贝叶斯滤波算法的推导过程：

$Bel({x_t}) = P({x_t}|{u_1},{z_1}\; \ldots ,{u_t},{z_t})$

$ = \eta \;{\kern 1pt} P({z_t}|{x_t},{u_1},{z_1}, \ldots ,{u_t})\;P({x_t}|{u_1},{z_1},\; \ldots ,{u_t}) ~~~~~~\rm{<—Bayes}$

$ = \eta \;{\kern 1pt} P({z_t}|{x_t})\;P({x_t}|{u_1},{z_1},\; \ldots ,{u_t})~~~~~~\rm{<—Markov}$

$ \!=\! \eta P({z_t}|{x_t})\int {P({x_t}|{u_1},{z_1},\! \ldots ,{u_t},{x_{t - 1}})} P({x_{t - 1}}|{u_1},{z_1}, \ldots ,{u_t})d{x_{t - 1}})~\rm{<—Total Prob}.$

$ = \eta P({z_t}|{x_t})\int {P({x_t}|{u_t},{x_{t - 1}})} P({x_{t - 1}}|{u_1},{z_1}, \ldots ,{u_t})d{x_{t - 1}})\; \rm{<—Markov}$

$ = \eta P({z_t}|{x_t})\int {P({x_t}|{u_t},{x_{t - 1}}){\mkern 1mu} } P({x_{t - 1}}|{u_1},{z_1}, \ldots ,{z_{t - 1}})d{x_{t - 1}})\; \rm{<—Markov}$

$ = \eta P({z_t}|{x_t})\int {P({x_t}|{u_t},{x_{t - 1}})} Bel({x_{t - 1}})\;d{x_{t - 1}}$

其中第一步采用贝叶斯公式展开，第二步使用Markov性质($z_t$仅由$x_t$决定)；第三步使用全概率公式对$x_{t-1}$进行展开；第四步继续使用Markov性质($x_t$仅由$x_{t-1}$和$u_t$决定)；第五步继续使用Markov性质，因为$x_{t-1}$同$u_t$无关，最终得到$Bel(x_t)$的递推公式。

可见递推公式中分为两个步骤，$\int {P({x_t}|{u_t},{x_{t - 1}})} Bel({x_{t - 1}})\;d{x_{t - 1}}$部分是基于$x_{t-1}, u_t$预测$x_t$的状态；$\eta P({z_t}|{x_t})$部分是基于观测$z_t$更新状态$x_t$.

4.3 Bayes滤波算法流程

所以，Bayes滤波的算法流程图如图5所示。如果$d$是观测，则进行一次状态更新，如果$d$是动作，则进行一次状态预测。

图5. Bayes滤波的算法流程

我们看到，在进行状态预测时，需要对所有可能的$x’$状态进行遍历，使得基本的Bayes模型在计算上成本是较高的。

4.3 Bayes滤波算法的应用

Bayes滤波方法是很多实用算法的基础，例如：

Kalman滤波
扩展Kalman滤波
信息滤波
粒子滤波

等，我们在下一节介绍Kalman滤波。

参考文献

[1]. Sebastian Thrun, Wolfram Burgard, Dieter Fox, Probabilistic Robotics, 2002, The MIT Press.

posted @ 2016-10-26 08:41 王永才阅读(38156) 评论(11) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

机器人感知、群智感知、图结构计算与优化算法

深入讲解相关的算法，并给出具体的示例代码。