K-D Tree
定义
K-D Tree 一个维护 \(k\) 维空间内的若干个点的数据结构。最常见的问题是在二维平面内,所以最常用的是 2-D Tree。
在结点数 \(n\) 远大于 \(2^k\) 时,应用 k-D Tree 的时间效率很好。
k-D Tree 的结构类似二叉搜索树,每个节点都对应 \(k\) 维空间内的一个点。其每个子树中的点都在一个 \(k\) 维的超长方体内,这个超长方体内的所有点也都在这个子树中。
建树
为了更具象的了解该数据结构,先以 2-D Tree 为例介绍。
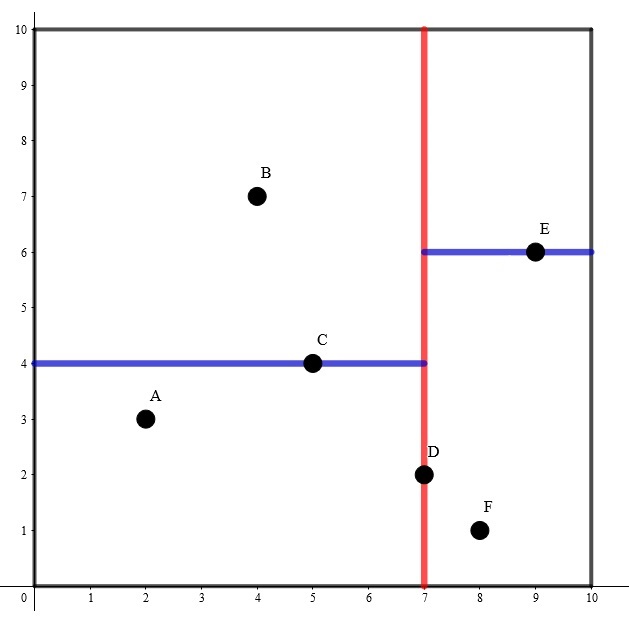
在以上的二维平面中共有6个点,我们可以从任意一个维度开始建树。
我们不妨从x轴这一维度开始,首先找到所有点中横坐标中位数的那个点,即点D。然后将x维度分割开成为左右两部分,左边递归的进入左子树,并且换一个维度重复上述的建树过程:
- 找到A,B,C三个点中纵坐标的中位数,即点C,将y维度分割开成为上下两部分,此时发现新分割出来的长方形中只有一个节点,递归结束;
- 右子树同理,找到E,F三个点中纵坐标的中位数,即点E,将y维度分割开成为上下两部分,此时发现新分割出来的长方形中只有一个节点(或没有节点),递归结束。
在上述过程中每次在维度上选择切割点时选择该维度上的中位数,这样可以保证每次分成的左右子树大小尽量相等。
而选择维度的方法有多种:
- 轮换法:每一次递归就换到下一个维度。
- 随机法:每一次递归随机出一个 \(w \in [1,k] \cap Z\),将第 \(w\) 维分割。
- 方差法:每次选择的切割维度是方差最大的维度,这样可以满足其内部点的分布的差异度最大。
- 作差法,计算出每一维最大最小值的差,选择差值最大的那一维度切割。
可以看出上述过程使用的是轮换法,方差法和作差法较为合理,更不容易被卡掉,但码量比随机法和轮换法要大,实际选择时依需而定。
现在,构建 k-D Tree 时间复杂度的瓶颈在于快速选出一个维度上的中位数,并将在该维度上的值小于该中位数的置于中位数的左边,其余置于右边。如果每次都使用 sort 函数对该维度进行排序,时间复杂度是 \(O(n\log^2 n)\) 的。事实上,单次找出 \(n\) 个元素中的中位数并将中位数置于排序后正确的位置的复杂度可以达到 \(O(n)\)。
我们来回顾一下快速排序的思想。每次我们选出一个数,将小于该数的置于该数的左边,大于该数的置于该数的右边,保证该数在排好序后正确的位置上,然后递归排序左侧和右侧的值。这样的期望复杂度是 \(O(n\log n)\) 的。但是由于 k-D Tree 只要求要中位数在排序后正确的位置上,所以我们只需要递归排序包含中位数的 一侧。可以证明,这样的期望复杂度是 \(O(n)\) 的。在 algorithm 库中,有一个实现相同功能的函数 nth_element(),要找到 \(s[l]\) 和 \(s[r]\) 之间的值按照排序规则 cmp 排序后在 \(s[mid]\) 位置上的值,并保证 \(s[mid]\) 左边的值小于 \(s[mid]\),右边的值大于 \(s[mid]\),只需写 nth_element(s+l,s+mid,s+r+1,cmp)。
借助这种思想,构建 k-D Tree 时间复杂度是 \(O(n\log n)\) 的。
应用
那么如何用 k-D Tree 解决问题呢,我们以一道例题为例。
题目描述
给定平面上 \(n\) 个点,找出其中的一对点的距离,使得在这 \(n\) 个点的所有点对中,该距离为所有点对中最小的
输入格式
第一行:\(n\) ,保证 \(2\le n\le 200000\)。
接下来 \(n\) 行:每行两个实数:\(x\ y\) 表示一个点的行坐标和列坐标,中间用一个空格隔开。
输出格式
仅一行,一个实数,表示最短距离,精确到小数点后面 4 位。
说明/提示
数据保证 \(0\le x,y\le 10^9\)
我们可以先建出 k-D Tree,对于树上每个节点我们考虑维护一个最小的矩形使得该子树内所有节点都在矩形内或矩形上。
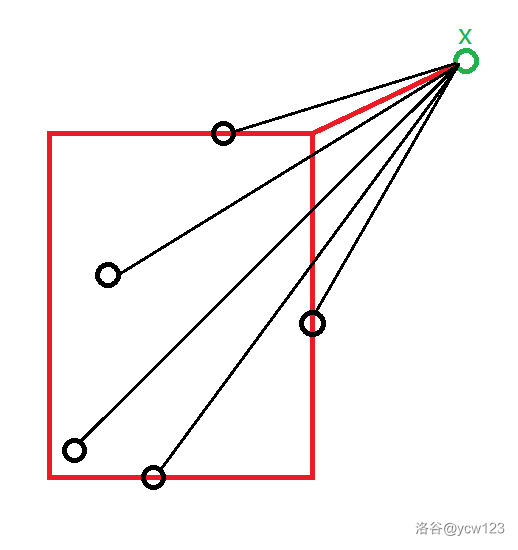
比如我们考虑一个节点 \(x\) 离它最近的节点。
不难发现,\(x\) 到矩形的距离(即图中红色的线段),一定小于等于该矩形内(上)所有节点到 \(x\) 的距离(即图中黑色的线段),若我们当前已经找到的最近节点到 \(x\) 的距离 \(mindis\) 小于等于 \(x\) 到矩形的距离,那么矩形内(上)的节点一定不能更新 \(mindis\)。
这样我们通过维护最小矩形,在查询一个点到这些点的最小距离时,就可以从 k-D Tree 的根节点开始递归遍历,在进入儿子节点前,我们先判断该节点维护的最小矩形到 \(x\) 的距离是否小于已经得到的最小值,若不是,那我们就不进入到这个儿子节点中,从而实现剪枝。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int n,root;
double ans=0x3f3f3f3f3f3f3f3f;
struct Point{
double x,y;
}p[N];
struct node{
int l,r,d;//左儿子编号,右儿子编号,切割维度
int L,R,D,U;//分别代表矩形上下左右四条边
}kt[N<<4];
double pow2(double x){return x*x;}
//两点距离,为了减少常数我们可以不开平方
double dis(int a,int b){return pow2(p[a].x-p[b].x)+pow2(p[a].y-p[b].y);}
bool cmpx(Point a,Point b){return a.x<b.x;}
bool cmpy(Point a,Point b){return a.y<b.y;}
void update(int x) {//维护最小矩形
kt[x].L=kt[x].R=p[x].x;
kt[x].D=kt[x].U=p[x].y;
if (kt[x].l){
node &ls=kt[kt[x].l];
kt[x].L=min(kt[x].L,ls.L);
kt[x].R=max(kt[x].R,ls.R);
kt[x].D=min(kt[x].D,ls.D);
kt[x].U=max(kt[x].U,ls.U);
}
if (kt[x].r){
node &rs=kt[kt[x].r];
kt[x].L=min(kt[x].L,rs.L);
kt[x].R=max(kt[x].R,rs.R);
kt[x].D=min(kt[x].D,rs.D);
kt[x].U=max(kt[x].U,rs.U);
}
}
int build(int l,int r){//建树
if(l>r)return 0;//没有节点,返回
if(l==r){//只有一个节点,维护矩形后返回
update(l);
return l;
}
int mid=l+r>>1;
node &x=kt[mid];
double avx=0,avy=0,vax=0,vay=0;//方差法选择切割维度
for(int i=l;i<=r;i++) avx+=p[i].x,avy+=p[i].y;
avx/=(double)(r-l+1),avy/=(double)(r-l+1);
for(int i=l;i<=r;i++){
vax+=pow2(p[i].x-avx);
vay+=pow2(p[i].y-avy);
}
if(vax>=vay) x.d=1,nth_element(p+l,p+mid,p+r+1,cmpx);//找中位数
else x.d=2,nth_element(p+l,p+mid,p+r+1,cmpy);
x.l=build(l,mid-1),x.r=build(mid+1,r);//递归建树
update(mid);
return mid;
}
double f(int a, int b) {//计算点到矩形的距离
auto &o = kt[b];
double ret = 0;
if (o.L > p[a].x) ret += (o.L - p[a].x) * (o.L - p[a].x);
if (o.R < p[a].x) ret += (p[a].x - o.R) * (p[a].x - o.R);
if (o.D > p[a].y) ret += (o.D - p[a].y) * (o.D - p[a].y);
if (o.U < p[a].y) ret += (p[a].y - o.U) * (p[a].y - o.U);
return ret;
}
void query(int x,int u){
//因为我们建树时将所有点都放进去了因此要判断自己不能计算和自己的距离
if(u!=x) ans=min(ans,dis(x,u));
if(!(kt[x].l+kt[x].r)) return;//叶子结点,返回
double disl=kt[x].l?f(u,kt[x].l):inf,disr=kt[x].r?f(u,kt[x].r):inf;//计算到左右矩形的距离
//如果左右有一个儿子不存在,要赋值为最大值
if(disl<disr){
if(disl<ans) query(kt[x].l,u);
if(disr<ans) query(kt[x].r,u);
}else{
if(disr<ans) query(kt[x].r,u);
if(disl<ans) query(kt[x].l,u);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
double x=0,y=0;
cin>>x>>y;
p[i]=Point{x,y};
}
root=build(1,n);
for(int i=1;i<=n;i++) query(root,i);
printf("%.4f\n",sqrt(ans));
return 0;
}
另一种更为优雅方便扩展到多维的写法(码量也少)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=200005,M=2;
const long long inf=0x3f3f3f3f3f3f3f3f;
int n,root,WD;
int ans=0x3f3f3f3f3f3f3f3f;
struct Point{
double x[2];
}p[N];
struct node{
int l,r,d;//左儿子编号,右儿子编号,切割维度
int mi[2],ma[2];//分别代表矩形上下左右四条边
}kt[N<<4];
double pow2(double x){return x*x;}
//两点距离,为了减少常数我们可以不开平方
int dis(int a,int b){
int res=0;
for(int w=0;w<M;w++) res+=pow2(p[a].x[w]-p[b].x[w]);
return res;
}
bool cmp(Point a,Point b){return a.x[WD]<b.x[WD];}
void update(int x) {//维护最小矩形
for(int w=0;w<M;w++) kt[x].mi[w]=kt[x].ma[w]=p[x].x[w];
if (kt[x].l){
int &ls=kt[x].l;
for(int w=0;w<M;w++)
kt[x].mi[w]=min(kt[x].mi[w],kt[ls].mi[w]),
kt[x].ma[w]=max(kt[x].ma[w],kt[ls].ma[w]);
}
if (kt[x].r){
int &rs=kt[x].r;
for(int w=0;w<M;w++)
kt[x].mi[w]=min(kt[x].mi[w],kt[rs].mi[w]),
kt[x].ma[w]=max(kt[x].ma[w],kt[rs].ma[w]);
}
}
int build(int l,int r,int wd){//建树
if(l>r) return 0;//没有节点,返回
if(l==r){//只有一个节点,维护矩形后返回
update(l);return l;
}
int mid=l+r>>1;
node &x=kt[mid];WD=wd;//轮换法
x.d=wd,nth_element(p+l,p+mid,p+r+1,cmp);//找中位数
x.l=build(l,mid-1,wd^1),x.r=build(mid+1,r,wd^1);//递归建树
update(mid);
return mid;
}
int f(int a, int b) {//计算点到矩形的距离
double ret = 0;
for(int w=0;w<M;w++) {
if (kt[b].mi[w] > p[a].x[w]) ret += (kt[b].mi[w] - p[a].x[w]) * (kt[b].mi[w] - p[a].x[w]);
if (kt[b].ma[w] < p[a].x[w]) ret += (p[a].x[w] - kt[b].ma[w]) * (p[a].x[w] - kt[b].ma[w]);
}
return ret;
}
void query(int x,int u){
//因为我们建树时将所有点都放进去了因此要判断自己不能计算和自己的距离
if(u!=x) ans=min(ans,dis(x,u));
if(!(kt[x].l+kt[x].r)) return;//叶子结点,返回
int disl=kt[x].l?f(u,kt[x].l):inf,disr=kt[x].r?f(u,kt[x].r):inf;//计算到左右矩形的距离
//如果左右有一个儿子不存在,要赋值为最大值
if(disl<disr){
if(disl<ans) query(kt[x].l,u);
if(disr<ans) query(kt[x].r,u);
}else{
if(disr<ans) query(kt[x].r,u);
if(disl<ans) query(kt[x].l,u);
}
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
double x=0,y=0;
cin>>x>>y;
p[i]=Point{x,y};
}
root=build(1,n,0);
for(int i=1;i<=n;i++) query(root,i);
printf("%.4f\n",sqrt(ans));
return 0;
}
注意:虽然以上使用的种种优化,但是使用 k-D Tree 单次查询最近点的时间复杂度最坏还是 \(O(n)\) 的,但不失为一种优秀的骗分算法,使用时请注意。
插入/删除
如果维护的这个 \(k\) 维点集是可变的,即可能会插入或删除一些点,此时 k-D Tree 的平衡性无法保证。由于 k-D Tree 的构造,不能支持旋转,类似与 FHQ Treap 的随机优先级也不能保证其复杂度,可以保证平衡性的手段只有类似于 替罪羊树 的重构思想。
我们引入一个重构常数 \(\alpha\),对于 k-D Tree 上的一个结点 \(x\),若其有一个子树的结点数在以 \(x\) 为根的子树的结点数中的占比大于 \(\alpha\),则认为以 \(x\) 为根的子树是不平衡的,需要重构。重构时,先遍历子树求出一个序列,然后用以上描述的方法建出一棵 k-D Tree,代替原来不平衡的子树。
在插入一个 \(k\) 维点时,先根据记录的分割维度和分割点判断应该继续插入到左子树还是右子树,如果到达了空结点,新建一个结点代替这个空结点。成功插入结点后回溯插入的过程,维护结点的信息,如果发现当前的子树不平衡,则重构当前子树。
code:
//动态插入可以将树上每个节点对应的点存下,并且要维护子树大小siz
int newnode(){//rub:节点回收
if(top) {
kt[rub[top]]={0,0,0,0,0,0,0,0,0,0,0,0};
return rub[top--];
}
else return ++tot;
}
void TtoL(int x,int &count) { //Tree to Line 即把树上数据存在序列中
if(!x) return;
if(kt[x].l) TtoL(kt[x].l,count);//递归存储左子树
tmp[++count]=kt[x].tp;//存储当前节点
rub[++top]=x;
if(kt[x].r) TtoL(kt[x].r,count);//递归存储右子树
return;
}
void rebuild(int &x,int wd) {
if(alpha * kt[x].siz > (double)max(kt[kt[x].l].siz,kt[kt[x].r].siz)) return;
int count=0;
TtoL(x,count);//先打散
x=build(1,count,wd);//再重构
return;
}
void insert(int &x,Point v,int wd) {//轮换法
if (!x) {
x = newnode();
kt[x].tp=v;
update(x);
return;
}
rebuild(x,wd);
if(kt[x].tp.x[wd]<v.x[wd]) insert(kt[x].r,v,wd^1);
else insert(kt[x].l,v,wd^1);
update(x);
}
如果还有删除操作,则使用 惰性删除,即删除一个结点时打上删除标记,而保留其在 k-D Tree 上的位置。如果这样写,当未删除的结点数在以 x 为根的子树中的占比小于 \(\alpha\) 时,同样认为这个子树是不平衡的,需要重构。
类似于替罪羊树,带重构的 k-D Tree 的树高仍然是 \(O(\log n)\) 的。
来看几道题
题目描述
已知平面内 \(N\) 个点的坐标,求欧氏距离下的第 \(K\) 远点对。
两个点 \(P(x_1,y_1)\) 和 \(Q(x_2,y_2)\) 的欧氏距离定义为 \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)输入格式
输入文件第一行为用空格隔开的两个整数 \(N,K\)。
接下来 \(N\) 行,每行两个整数 \(X,Y\),表示一个点的坐标。
输出格式
输出文件第一行为一个整数,表示第 \(K\) 远点对的距离的平方(一定是个整数)。
和上一道例题类似,从最近点对变成了 \(k\) 远点对,这时就要比较到矩形的最远距离。用一个小根堆来维护当前找到的前 \(k\) 远点对之间的距离,如果当前找到的点对距离大于堆顶,则弹出堆顶并插入这个距离,同样的,使用堆顶的距离来剪枝。
可以通过动态插入的方式,每插入一个点前查询该点到前面所有点的距离,维护 \(k\) 远点。
code:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=300005;
int n,root,m,lst,top,tot,WD,ans,K;
double alpha=0.75;
struct Point {
int x[2];
Point(int x0 = 0,int x1 = 0){
x[0] = x0;x[1] = x1;
}
}tmp[N];
int rub[N];
struct node {
int l,r,d,siz;
int mi[2],ma[2];
Point tp;
} kt[1000005];
int newnode(){
if(top) {
kt[rub[top]]=(node){0,0,0,0,0,0,0,0,Point()};
return rub[top--];
}
else return ++tot;
}
priority_queue<int,vector<int>,greater<int> > Q;
bool operator < (Point a,Point b) {
return a.x[WD]<b.x[WD];
}
void TtoL(int x,int &count) { //Tree to Line 即把树上数据存在序列中
if(!x) return;
if(kt[x].l) TtoL(kt[x].l,count);//递归存储左子树
tmp[++count]=kt[x].tp;//存储当前节点
rub[++top]=x;
if(kt[x].r) TtoL(kt[x].r,count);//递归存储右子树
return;
}
void update(int x) {
int &ls=kt[x].l,&rs=kt[x].r;
kt[x].siz=kt[ls].siz+kt[rs].siz+1;
for(int W=0;W<=1;W++) {
kt[x].mi[W]=kt[x].ma[W]=kt[x].tp.x[W];
if(ls) kt[x].mi[W]=min(kt[x].mi[W],kt[ls].mi[W]),kt[x].ma[W]=max(kt[x].ma[W],kt[ls].ma[W]);
if(rs) kt[x].mi[W]=min(kt[x].mi[W],kt[rs].mi[W]),kt[x].ma[W]=max(kt[x].ma[W],kt[rs].ma[W]);
}
}
int build(int l,int r,int wd) {
if(l>r)return 0;
if(l==r) {int x=newnode();kt[x].tp=tmp[l];update(x);return x;}
int mid=l+r>>1,x=newnode();
WD=wd,nth_element(tmp+l,tmp+mid,tmp+r+1),kt[x].tp=tmp[mid];
kt[x].l=build(l,mid-1,wd^1),kt[x].r=build(mid+1,r,wd^1);
update(x);return x;
}
void rebuild(int &x,int wd) {
if(alpha * kt[x].siz > (double)max(kt[kt[x].l].siz,kt[kt[x].r].siz)) return;
int count=0;
TtoL(x,count);//先打散
x=build(1,count,wd);//再重构
return;
}
void insert(int &x,Point v,int wd) {
if (!x) {
x = newnode();
kt[x].tp=v;
update(x);
return;
}
rebuild(x,wd);
if(kt[x].tp.x[wd]<v.x[wd]) insert(kt[x].r,v,wd^1);
else insert(kt[x].l,v,wd^1);
update(x);
}
int dis(Point a,Point b){
int res=0;
for(int W=0;W<=1;W++) res+=(a.x[W]-b.x[W])*(a.x[W]-b.x[W]);
return res;
}
int f(Point a, int b) {
node &o=kt[b];
int res=0;
for(int W=0;W<=1;W++) {
res+=max((o.mi[W]-a.x[W])*(o.mi[W]-a.x[W]),(a.x[W]-o.ma[W])*(a.x[W]-o.ma[W]));
}
return res;
}
void query(int x,Point u){
if(!x) return;
int DIS=dis(kt[x].tp,u);
Q.push(DIS);
while(Q.size()>K) Q.pop();
if(!(kt[x].l+kt[x].r)) return;
int disl=kt[x].l?f(u,kt[x].l):-1,disr=kt[x].r?f(u,kt[x].r):-1,Qmin=-1;
if(Q.size()) Qmin=Q.top();
if(disl>disr){
if(disl>Qmin) query(kt[x].l,u);
while(Q.size()>K) Q.pop();
if(Q.size()) Qmin=Q.top();
if(disr>Qmin) query(kt[x].r,u);
}else{
if(disr>Qmin) query(kt[x].r,u);
while(Q.size()>K) Q.pop();
if(Q.size()) Qmin=Q.top();
if(disl>Qmin) query(kt[x].l,u);
}
}
signed main() {
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>n>>K;
int opt=0,xx,yy,vv;
for(int i=1;i<=n;i++){
cin>>xx>>yy;
query(root,Point(xx,yy));
insert(root,Point(xx,yy),0);
}
cout<<Q.top();
}
除了点对间距离的问题,k-D Tree 配合线段树还可以维护某个区域内的点的个数(或点权和)。
例题luogu P4148 简单题
在一个初始值全为 \(0\) 的 \(n\times n\) 的二维矩阵上,进行 \(q\) 次操作,每次操作为以下两种之一:
1 x y A:将坐标 \((x,y)\) 上的数加上 \(A\)。
2 x1 y1 x2 y2:输出以 \((x1,y1)\) 为左下角,\((x2,y2)\) 为右上角的矩形内(包括矩形边界)的数字和。
强制在线。内存限制 20M。保证答案及所有过程量在int范围内。
\(1≤N≤5×10^5\),操作数不超过 \(2\times 10^5\)个
20M 的空间卡掉了所有树套树,强制在线卡掉了 CDQ 分治,只能使用 k-D Tree。
构建 2-D Tree,支持两种操作:添加一个 2 维点;查询矩形区域内的所有点的权值和。可以使用 带重构 的 k-D Tree 实现。
在查询矩形区域内的所有点的权值和时,仍然需要记录子树内每一维度上的坐标的最大值和最小值。如果当前子树对应的矩形与所求矩形没有交点,则不继续搜索其子树;如果当前子树对应的矩形完全包含在所求矩形内,返回当前子树内所有点的权值和;否则,判断当前点是否在所求矩形内,更新答案并递归在左右子树中查找答案。
已经证明,如果在 2-D 树上进行矩阵查询操作,已经被完全覆盖的子树不会继续查询,则单次查询时间复杂度是最优 \(O(\log n)\),最坏 \(O(\sqrt n)\) 的。将结论扩展到 k 维的情况,则最坏时间复杂度是 \(O(n^{1-\frac 1 k})\) 的。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int n,root,xl,xr,yl,yr,lst,top,tot,WD;
double alpha=0.75;
struct Point {
int x[2],v;
}tmp[N];
int rub[N];
struct node {
int l,r,d,siz,sum;
int mi[2],ma[2];
Point tp;
} kt[700005];
int newnode(){
if(top) {
kt[rub[top]]={0,0,0,0,0,0,0,0,0,0,0,0};
return rub[top--];
}
else return ++tot;
}
bool operator < (Point a,Point b) {
return a.x[WD]<b.x[WD];
}
void TtoL(int x,int &count) { //Tree to Line 即把树上数据存在序列中
if(!x) return;
if(kt[x].l) TtoL(kt[x].l,count);//递归存储左子树
tmp[++count]=kt[x].tp;//存储当前节点
rub[++top]=x;
if(kt[x].r) TtoL(kt[x].r,count);//递归存储右子树
return;
}
void update(int x) {
int &ls=kt[x].l,&rs=kt[x].r;
kt[x].siz=kt[ls].siz+kt[rs].siz+1;
kt[x].sum=kt[ls].sum+kt[rs].sum+kt[x].tp.v;
for(int W=0;W<=1;W++) {
kt[x].mi[W]=kt[x].ma[W]=kt[x].tp.x[W];
if(ls) kt[x].mi[W]=min(kt[x].mi[W],kt[ls].mi[W]),kt[x].ma[W]=max(kt[x].ma[W],kt[ls].ma[W]);
if(rs) kt[x].mi[W]=min(kt[x].mi[W],kt[rs].mi[W]),kt[x].ma[W]=max(kt[x].ma[W],kt[rs].ma[W]);
}
}
int build(int l,int r,int wd) {
if(l>r)return 0;
if(l==r) {int x=newnode();kt[x].tp=tmp[l];update(x);return x;}
int mid=l+r>>1,x=newnode();
WD=wd,nth_element(tmp+l,tmp+mid,tmp+r+1),kt[x].tp=tmp[mid];
kt[x].l=build(l,mid-1,wd^1),kt[x].r=build(mid+1,r,wd^1);
update(x);return x;
}
void rebuild(int &x,int wd) {
if(alpha * kt[x].siz > (double)max(kt[kt[x].l].siz,kt[kt[x].r].siz)) return;
int count=0;
TtoL(x,count);//先打散
x=build(1,count,wd);//再重构
return;
}
void insert(int &x,Point v,int wd) {
if (!x) {
x = newnode();
kt[x].tp=v;
update(x);
return;
}
rebuild(x,wd);
if(kt[x].tp.x[wd]<v.x[wd]) insert(kt[x].r,v,wd^1);
else insert(kt[x].l,v,wd^1);
update(x);
}
int query(int x) {
if (!x || xr < kt[x].mi[0] || xl > kt[x].ma[0] || yr < kt[x].mi[1] || yl > kt[x].ma[1]) return 0;
if (xl <= kt[x].mi[0] && kt[x].ma[0] <= xr && yl <= kt[x].mi[1] && kt[x].ma[1] <= yr) return kt[x].sum;
int ret = 0;
if (xl <= kt[x].tp.x[0] && kt[x].tp.x[0] <= xr && yl <= kt[x].tp.x[1] && kt[x].tp.x[1] <= yr)
ret += kt[x].tp.v;
return query(kt[x].l) + query(kt[x].r) + ret;
}
int main() {
scanf("%d", &n);
int opt=0,xx,yy,vv;
while (~scanf("%d", &opt)) {
if (opt == 1) {
scanf("%d%d%d", &xx, &yy, &vv);
xx ^= lst,yy ^= lst,vv ^= lst;
insert(root,Point{{xx,yy},vv},0);
}
if (opt == 2) {
scanf("%d%d%d%d", &xl, &yl, &xr, &yr);
xl ^= lst,yl ^= lst,xr ^= lst,yr ^= lst;
printf("%d\n", lst = query(root));
}
if (opt == 3) return 0;
}
}


