欧拉路径与欧拉回路
Luogu P7771 【模板】欧拉路径
题意
给定一个 \(n\) 个点 \(m\) 条边的有向图，求该图字典序最小的欧拉路径。
数据范围
对于 50% 的数据，\(n,m\le 10^3\)。
对于 100% 的数据，\(1\leq u,v\leq n\leq 10^5\)，\(m\leq 2\times 10^5\)。
Solution:
来系统地整理一下有关欧拉回路和欧拉路径的问题。
什么是欧拉路径？
通过图中所有边恰好一次且行遍所有顶点（允许多次经过同一个点）的通路称为欧拉路径。即一笔画。
如果这条路径的起点和终点重合，那么就是欧拉回路。
如何判断图是否有欧拉回路或者欧拉路径？
-
无向图：因为欧拉路径中，除了起点与终点以外，任意点的“进”“出”次数相等，所以除了两个点为奇点（度数为奇数的点）（终点和起点）以外，其它点的度数均为偶数。
如果是欧拉回路，奇点的个数应该为0。
-
有向图：欧拉路径中，最多只有两个点的入度不等于出度。起点出度比入度大1，终点入度比出度大1。
如果是欧拉回路，所有点的 入度 = 出度 。
寻找欧拉回路或欧拉路径的算法有？
Fluery 算法和 Hierholzer 算法。
这里只讲解 Hierholzer 算法。
Hierholzer 算法自动寻找欧拉回路，在找不到欧拉回路的情况下会找到欧拉路径。前提是得给它指定好起点。
- 算法流程（无向图）：
-
判断奇点数。奇点数若为0则任意指定起点，奇点数若为2则指定起点为奇点。
-
开始递归函数 Hierholzer(x):
循环寻找与 \(x\) 相连的边 \(x \to u\):
删除 \(x \to u\)
删除 \(u \to x\)
Hierholzer(u);
回溯时将 \(x\) 插入答案队列之中
-
倒序输出答案队列
举个栗子
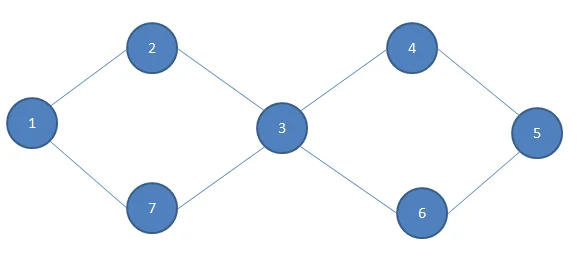
对于该图，算法的执行流程如下：
step1： 找到该图没有奇点，从1开始进行 Hierholzer 算法。
step2： 删边 \(1 \to 2\) 递归到2
step3： 删边 \(2 \to 3\) 递归到3
step4： 删边 \(3 \to 7\) 递归到7
step5： 删边 \(7 \to 1\) 递归到1
step6： 1无边，1加入队列，返回
step7： 7加入队列，返回
step8： 删边 \(3 \to 4\) 递归到4
step9： 删边 \(4 \to 5\) 递归到5
step10： 删边 \(5 \to 6\) 递归到6
step11： 删边 \(6 \to 3\) 递归到3
step12： 3加入队列，返回
step13： 6加入队列，返回
step14： 5加入队列，返回
step15： 4加入队列，返回
step16： 3加入队列，返回
step17： 2加入队列，返回
step18： 1加入队列，返回
答案队列为：1 7 3 6 5 4 3 2 1。反向输出即为答案。
有向图除判断是否存在有一点点不同以外同理。
对于该【模板】题，要求按字典序输出答案。所以起点首先要选的尽量小，然后在边的储存上面加一点小 trick。
使用邻接表储存图时，除了用链式前向星还可以用 vector 储存。我们可以把 vector 排序，这样就可以保证该点前往的下一个点是最小值，同时保证了答案的最小值。
sort(a.begin(),a.end(),cmp); //vector排序方法
基于上面对算法的分析，我们可以写出 dfs 基本框架了：
void dfs(int x){
for(){ //遍历所有与x相邻的点u
if(!vis[u]){ //x与u的这条边没被访问过
vis[u]=1;
dfs(u); //递归与x相邻的点u
}
}
s.push(x); //没有边了,将x进入序列 (用栈处理倒序输出）
}
但对于本题来说，这样的时间复杂度过不去的。按照算法，我们不能走重复边，但如果每次都 vis 判断一遍，则会出现很多次访问同一条边，会被毒瘤数据卡掉。
处理：
对于任意一个点 \(u\) 来说，建完图之后访问边是有顺序的，我们新开一个数组 \(st\) 记录访问到哪个位置即可（即该删除哪个位置）。
Code
#include<bits/stdc++.h> //万能头文件
using namespace std;
struct node{
int u;
bool vis; //记录是否被访问过
};
int n,m;
vector<node> v[100010];
int in[100010],st[100010]; //in表示每个结点入度与出度的差（即入读-出度）
stack<int> s; //记录答案
void dfs(int x){
for(int i=0;i<v[x].size();i=max(i+1,st[x])){
if(v[x][i].vis) continue;
v[x][i].vis=1;
st[x]=i+1;
dfs(v[x][i].u);
}
s.push(x);
}
bool cmp(node a,node b){
return a.u<b.u;
}
int main(){
cin>>n>>m;
for(int i=1,x,y;i<=m;i++){
cin>>x>>y;
v[x].push_back(node{y,0});
in[y]++;
in[x]--;
}
int fb=0,fe=0,pb=1,pe;
for(int i=1;i<=n;i++){ //判断是否存在欧拉路径
if(in[i]>1||in[i]<-1) {
printf("No");
return 0;
}
if(in[i]==1) fe++,pe=i;
if(in[i]==-1) fb++,pb=i;
if(fb>1||fe>1) {
printf("No");
return 0;
}
}
for(int i=1;i<=n;i++) sort(v[i].begin(),v[i].end(),cmp);
dfs(pb);
while(s.size()){
printf("%d ",s.top());
s.pop();
}
return 0;
}
