并查集
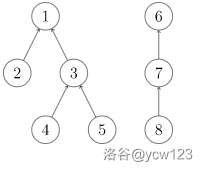
并查集(Disjoint--Set) 是一种可以动态维护若干个不重叠的集合，并支持合并与查询的数据结构。详细地说，并查集包括如下两个基本操作：
-
\(Find\)， 查询一个元素属于哪一个集合。
-
\(Merge\)， 把两个集合合并成一个大集合。
为了具体实现并查集这种数据结构，我们首先需要定义集合的表示方法。
在并查集中，我们采用 “代表元” 法，即为每个集合选择一个固定的元素，作为整个集合的“代表”。
其次，我们需要定义归属关系的表示方法。
第一种思路是维护一个数组 \(f\) ，用 \(f[x]\) 保存元素 \(x\) 所在集合的“代表”。
这种方法可以快速查询元素的归属集合，但在合并时需要修改大量元素的 \(f\) 值，效率很低。
第二种思路是使用一个树形结构存储每个集合，树上的每个节点都是一个元素，树根是集合的代表元素。整个并查集实际上是一个森林(若干棵树)。我们仍然可以维护一个数组 \(fa\) 来记录这个森林，用 \(fa[x]\) 保存 \(x\) 的父节点。
特别地，令树根的 \(fa\) 值为它自己。
这样一来，在合并两个集合时，只需连接两个树根(令其中一个树根为另一个树根的节点，即 \(fa[root1] = root2\) )。
c++实现参考
int fa[MAXN]; // 记录某个人的爸爸是谁，特别规定，祖先的爸爸是他自己
int find(int x) {
// 寻找x的祖先
if (fa[x] == x) // 如果x是祖先则返回
return x;
else
return find(fa[x]); // 如果不是则x的爸爸问x的爷爷
}
不过在查询元素的归属时，需要从该元素开始通过 \(fa\) 存储的值不断递归访问父节点，直至到达树根。为了提高查询效率，并查集引入了路径压缩与按秩合并两种思想。
路径压缩与按秩合并
其实不难发现，我们之前讨论的第一种思路 （直接用数组 \(f\) 保存代表） 的查询效率很高，我们不妨把两种思路进行结合。
实际上，我们只关心每个集合对应的“树形结构”的根节点是什么，并不关心这棵树的具体形态——这意味着下图中的两颗树是等价的：
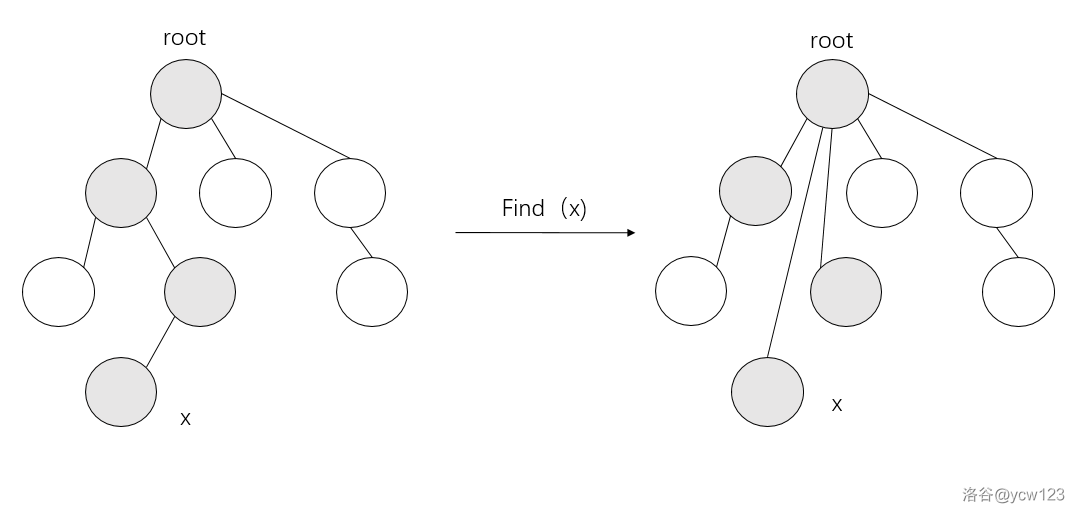
因此，我们可以 在每次执行 \(find\) 操作的同时，把访问过的每个节点（也就是所查询元素的每个祖先）都直接指向树根， 即把上图中左边那棵树变成右边那颗。
这种优化方法被称为路径压缩。采用路径压缩优化的并查集，每次 \(find\) 操作的均摊复杂度为 \(O(logN)\) 。
还有一种优化方法被称为按秩合并。
所谓 “秩”，一般有两种定义。有的资料把并查集中集合的 “秩” 定义为树的深度(未路径压缩时)。有的资料把集合的 “秩” 定义为集合的大小。
无论采取哪种定义，我们都可把集合的 “秩” 记录在 “代表元素”，也就是树根上。在合并时都把 “秩” 较小的树根作为 “秩” 较大的树根的子节点。
值得一提的是，当 “秩” 定义为集合的大小时，“按秩合并”也称为 “启发式合并” ，它是数据结构相关问题中一种重要的思想，应用非常广泛，不只局限于并查集中。
启发式合并的原则是：
把“小的结构”合到“大的结构”中，并且只增加“小的结构”的查询代价。
这样一来，把所有结构全部合并起来，增加的总代价不会超过 \(NlogN\) 故单独采用“按秩合并”优化的并查集，每次 \(find\) 操作的均摊复杂度也是 \(O(1ogN)\) 。
同时采用“路径压缩”和“按秩合并”优化并查集， 每次 \(find\) 操作的均摊复杂度可以进一步降低到 \(O(α(N))\) ，其中 \(α(N)\) 为反阿克曼函数，它是一个比“对数函数” \(logN\) 增长还要慢的函数，可近似为一个常数。
在实际应用中，我们一般只用路径压缩优化就足够了。接下来，我们对并查集的具体代码实现作一下具体说明。
-
并查集的存储
使用一个数组 \(fa\) 保存父节点（根的父节点设为自己）。
int fa[MAXN]; -
并查集的初始化
设有 \(n\) 个元素，起初所有元素各自构成一个独立的集合，即有 \(n\) 棵1个点的树。
for(int i=1;i<=n;i++) fa[i] = i; -
并查集的 \(find\) 操作
若 \(x\) 是树根，则 \(x\) 就是集合代表，否则递归访问 \(fa[x]\) 直至根节点。
int find(int x){ if(fa[x]==x) return x; return fa[x] = find(f[x]);//路径压缩，fa直接赋值为代表元素 } -
并查集的 \(Merde\) 操作
合并元素 \(x\) 和元素 \(y\) 所在的集合，等价于让 \(x\) 的树根作为 \(y\) 的树根的子节点。
void merge(int x,int y){ fa[find(x)] = find(y); }
并查集进阶
拓展域并查集
一般的并查集只能查找出各元素之间是否存在某一种相同的联系，如： \(a\) 和 \(b\) 是亲戚关系，\(b\) 和 \(c\) 是亲戚关系，这时就可以查找出 \(a\) 和 \(c\) 也存在亲戚关系。但如果存在多种相对的联系时一般的并查集就不行了，这时就需要对并查集进行拓展。即根据存在相对的关系数量把并查集的元素分出多份。
如：\(1\)~\(n\)各元素中，存在相同和相对的关系，那么就把各元素都分成 \(x\) 和 \(x+n\) 两部分，分别表示为和 \(x\) 相同的部分及和 \(x\) 相对的部分，当 \(x\) 和 \(y\) 相同时，则把 \(x\) 和 \(y\) 相连接，把 \(x+n\) 和 \(y+n\) 相连接 (\(x\) 和 \(y\) 相同也代表 \(x\) 相对的和 \(y\) 相对的是相同的)，当 \(x\) 和 \(y\) 相对时，则把 \(x\) 和 \(y+n\) 相连接，把 \(x+n\) 和 \(y\) 相连接(即 \(x\) 和 \(y\) 相对的是相同的，\(x\) 相对的和 \(y\) 是相同的)。
\(\large \textbf{题目描述}\)
S 城现有两座监狱，一共关押着 \(N\) 名罪犯，编号分别为 \(1-N\)。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 \(c\) 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 \(c\) 的冲突事件。
每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。
在详细考察了 \(N\) 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。
那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？
