最短路径问题---Dijkstra算法详解

0. 最短路径问题介绍

问题解释：

从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径

1. Dijkstra算法介绍

算法特点：

迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
算法的思路

Dijkstra算法采用的是一种贪心的策略

需要声明一个数组 $d i s$ 以及一个集合 $T$

$d i s [i]$ 表示源点到节点 $i$ 的最短距离

$T$ 中存储已经找到了最短路径的节点

初始时，源点 $s$ 的路径权重被赋为 0 $(d i s [s] = 0)$ 。若对于节点 $s$ 存在能直接到达的边 $s \to m$ ，则把 $d i s [m]$ 设为 $w$ ,同时把所有其他（ $s$ 不能直接到达的）节点的路径长度设为无穷大。初始时，集合 $T$ 只有顶点 $s$ 。

然后，从 $d i s$ 数组选择最小值，则该值就是源点 $s$ 到该值对应的顶点的最短路径，并且把该点加入到 $T$ 中，OK，此时完成一个顶点。

接着我们需要看看新加入的顶点是否可以到达其他顶点并且看看通过该顶点到达其他点的路径长度是否比当前的最短路径短，如果是，那么就替换这些顶点在 $d i s$ 中的值。

然后，又从 $d i s$ 中找出最小值，重复上述动作，直到 $T$ 中包含了图的所有顶点。

3、Dijkstra算法示例演示

求下图，从顶点 $v_{1}$ 到其他各个顶点的最短路径

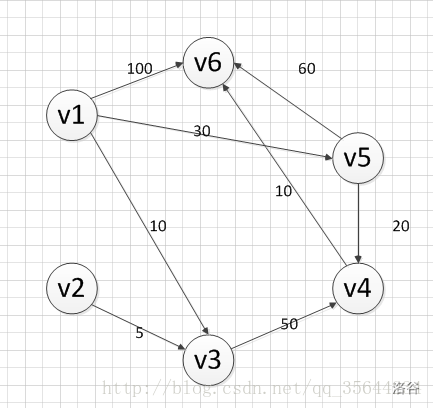
首先第一步，我们先声明一个dis数组，该数组初始化的值为（下标从1开始）：

下标	1	2	3	4	5	6
dis	0	∞	10	∞	30	100

我们的 $T$ 的初始化为： $T = {v_{1}}$

既然是求 $v_{1}$ 顶点到其余各个顶点的最短路程，就先找一个离 1 号顶点最近的顶点。通过数组 $d i s$ 可知当前离 $v_{1}$ 顶点最近是 $v_{3}$ 顶点。当选择了 2 号顶点后， $d i s [3]$ 的值就确定下来了，即 $v_{1}$ 顶点到 $v_{3}$ 顶点的最短路程就是当前 $d i s [3]$ 的值。将 $v_{3}$ 加入到 $T$ 中。

为什么呢？因为目前离 $v_{1}$ 顶点最近的是 $v_{3}$ 顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 $v_{1}$ 顶点到 $v_{3}$ 顶点的路程进一步缩短了。因为 $v_{1}$ 顶点到其它顶点的路程肯定没有 $v_{1}$ 到 $v_{3}$ 顶点短.

OK，既然确定了一个顶点的最短路径，下面我们就要根据这个新入的顶点 $v_{3}$ 会有出度，发现 $v_{3}$ 所连的边的有： $v_{3} \to v_{4}$ ，那么我们看看路径： $v_{1} \to v_{3} \to v_{4}$ 的长度是否比 $v_{1} \to v_{4}$ 短，其实这个已经是很明显的了，因为 $d i s [3]$ 代表的就是 $v_{1} \to v_{4}$ 的长度为无穷大，而 $v_{1} \to v_{3} \to v_{4}$ 的长度为：10+50=60，所以更新 $d i s [3]$ 的值,得到如下结果：

下标	1	2	3	4	5	6
dis	0	∞	10	60	30	100

然后，我们又从除 $d i s [3]$ 和 $d i s [1]$ 外的其他值中寻找最小值，发现 $d i s [5]$ 的值最小，通过之前是解释的原理，可以知道 $v_{1}$ 到 $v_{5}$ 的最短距离就是 $d i s [5]$ 的值，然后，我们把 $v_{5}$ 加入到集合 $T$ 中，然后考虑 $v_{5}$ 的出度是否会影响我们的数组 $d i s$ 的值， $v_{5}$ 有两条出度： $v_{5} \to v_{4}$ 和 $v_{5} \to v_{6}$ ，然后我们发现： $v_{1} \to v_{5} \to v_{4}$ 的长度为50，而 $d i s [4]$ 的值为60，所以我们要更新 $d i s [4]$ 的值。另外， $v_{1} \to v_{5} \to v_{6}$ 的长度为90，而 $d i s [6]$ 为100，所以我们需要更新 $d i s [6]$ 的值。更新后的 $d i s$ 数组如下：

下标	1	2	3	4	5	6
dis	0	∞	10	50	30	90

然后，继续从 $d i s$ 中选择未确定的顶点的值中选择一个最小的值，发现 $d i s [4]$ 的值是最小的，所以把 $v_{4}$ 加入到集合 $T$ 中，此时集合 $T = {v_{1}, v_{3}, v_{5}, v_{4}}$ ，然后考虑 $v_{4}$ 的出度是否会影响我们的数组 $d i s$ 的值， $v_{4}$ 有一条出度： $v_{4} \to v_{6}$ ，然后我们发现 $v_{1} \to v_{5} \to v_{4} \to v_{6}$ 的长度为60，而 $d i s [6]$ 的值为90，所以我们要更新 $d i s [6]$ 的值，更新后的 $d i s$ 数组如下：

下标	1	2	3	4	5	6
dis	0	∞	10	50	30	60

然后，我们使用同样原理，分别确定了 $v_{6}$ 和 $v_{2}$ 的最短路径，最后 $d i s$ 的数组的值如下：

下标	1	2	3	4	5	6
dis	0	∞	10	50	30	60

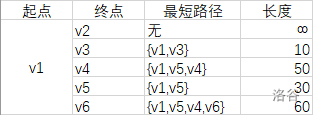
因此，从图中，我们可以发现 $v_{1} \to v_{2}$ 的值为 $\infty$ ，代表没有路径从 $v_{1}$ 到达 $v_{2}$ 。所以我们得到的最后的结果为：

4、Dijkstra算法代码实现：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=7010;
struct node{
	int i;
	int k;
	bool operator < (node a) const{
		return k>a.k;
	}
};
int n,m,s;
ll dis[maxn];
bool T[maxn];
priority_queue<node> q;
int head[maxn],to[2*maxn],nxt[2*maxn],w[2*maxn],cnt=1;
void add(int x,int y,int v){
	cnt++;
	to[cnt]=y;
	w[cnt]=v;
	nxt[cnt]=head[x];
	head[x]=cnt;
}
int main(){
	cin>>n>>m>>s;
	for(int i=1,x,y,v;i<=m;i++){
		cin>>x>>y>>v;
		add(x,y,v);
		add(y,x,v);
	}
	memset(dis,0x3f,sizeof(dis));
	dis[s]=0;
	q.push(node{s,0});
	while(q.size()){
		node h=q.top();
		int p=h.i;
		q.pop();
		if(T[p]) continue;
		T[p]=true;
		for(int i=head[p];i;i=nxt[i]){
			if(dis[p]+w[i]<dis[to[i]]&&!T[to[i]]){
				dis[to[i]]=dis[p]+w[i];
				q.push(node{to[i],dis[to[i]]});
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(dis[i]==0x3f3f3f3f3f3f3f3f) printf("-1\n");
		else printf("%lld\n",dis[i]);
	}
	return 0;
}