主席树（可持久化线段树）
主席树的定义与作用
主席树，也称可持久化线段树（主席树为什么叫主席树？据说因为它是一个名字缩写为 \(HJT\) 的神犇发明的，与当时主席的名字缩写一样......）
什么是可持久化线段树呢，即为一颗记录了所有更新过程的线段树。能够处理出从第 \(i\) 次更新到第 \(j\) 次更新的线段树变化。
前置知识
值域线段树
要学主席树，我们就要先学值域线段树。
值域线段树的区间存的并不是节点信息，而是在值在某一范围内的数的个数。
如图就是一棵值域线段树。
1号节点 存储的是 大于等于1小于等于4的数字个数
2号节点存储的是 大于等于1小于等于2的数字个数
3号节点存储的是 大于等于3小于等于4的数字个数
4号节点存储的是 等于1的数字个数
5号节点存储的是 等于2的数字个数
6号节点存储的是 等于3的数字个数
7号节点存储的是 等于4的数字个数
值域线段树的查询也挺简单的，若要查询这段区间内的第 \(k\) 大，只要比较当前元素的左子树大小加1（1是当前元素本身的大小）与询问的 \(k\)，若大于等于，就访问左子树，否则将 \(k\) 减去当前元素的左子树大小加1，然后访问右子树。
动态开点线段树
从值域线段树到主席树
上述值域线段树做法只能从所有数中找出第 \(k\) 大，如果我们的询问变成了 查询区间 [l,r] 内第 \(k\) 大的数 又该怎么办呢
考虑建 \(n\) 棵值域线段树，每棵值域线段树存储区间 [1,i] 的信息，这样一来，要查询 [l,r] 的第 \(k\) 大时，只要在查询的过程中，将第 \(r\) 棵值域线段树的信息减去第 \(l-1\) 棵值域线段树的信息即可，这利用了前缀和的思想。
但是建 \(n\) 棵值域线段树，不论是时间还是空间，复杂度都是相当劣的。怎样优化呢？
接下来的操作就是主席树的精妙所在了。
比如下面一组数，我们该如何对它进行操作呢？
3,5,8,6,7,2,1,4
我们建一棵值域线段数，将 \(3\) 放到里面
它会是下面这个样子
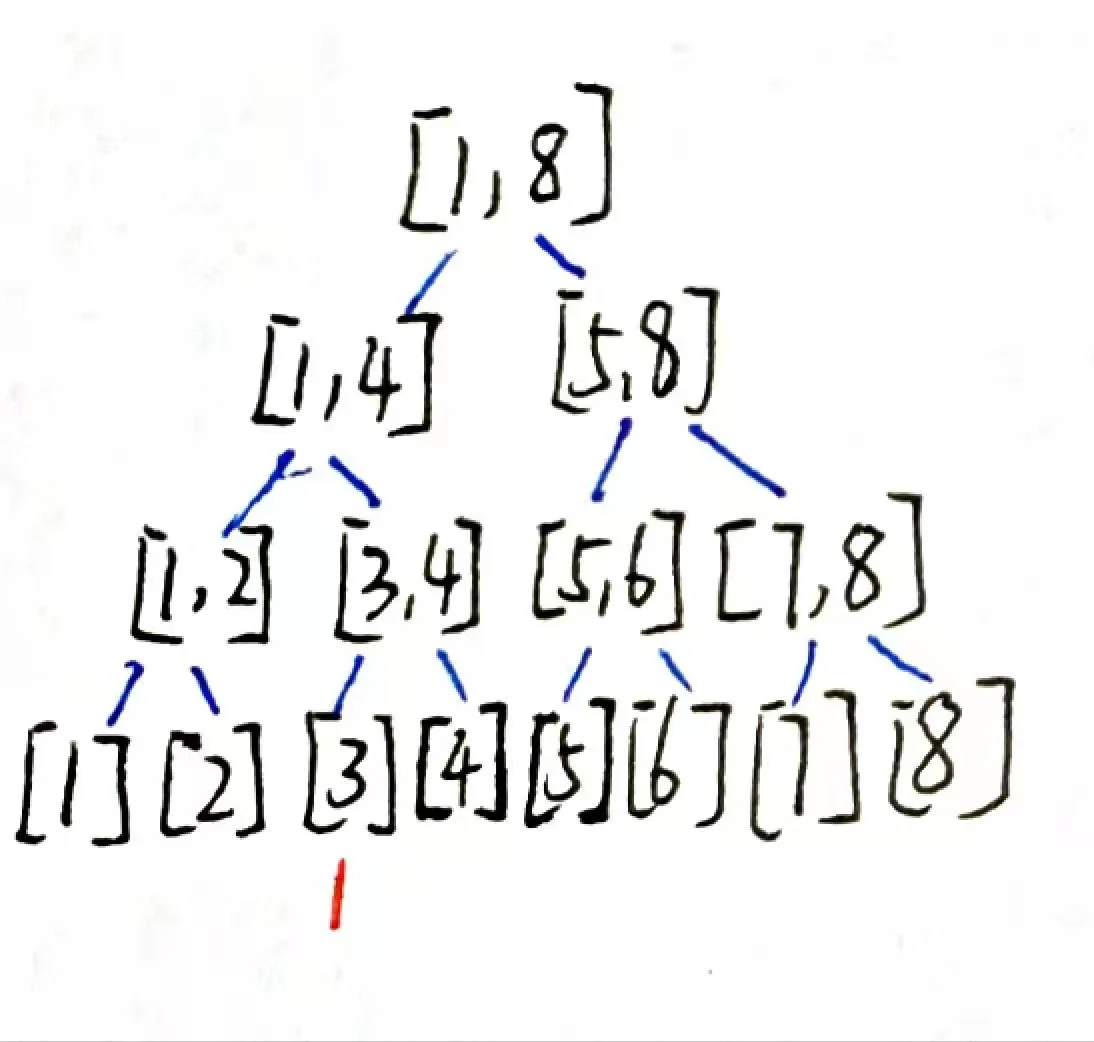
如果我们不做优化的话我们将继续建一棵树并把 \(5\) 放到里面
新的值域线段树会长这个样子
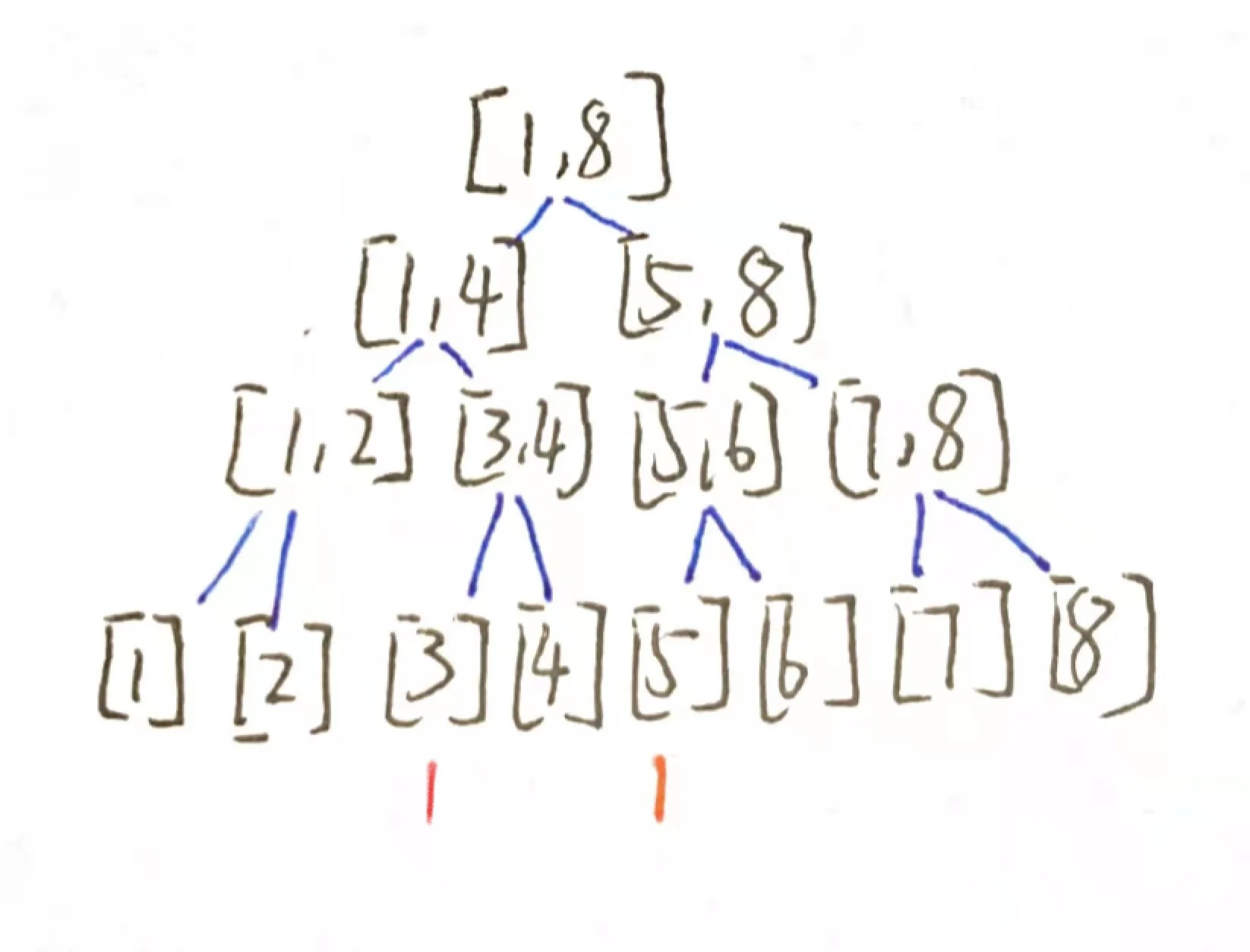
我们发现每次加入一个新的元素时更改的部分只会是一条链，而其他的部分则是无用的节点，自然的我们就想到能否让这两棵树共用这部分节点来减少节点的数量和建树的时间。
怎么操作呢？我们先建根结点，递归去看左孩子和右孩子，会发现左孩子的信息和上一棵树的是一样的，所以让他的左孩子直接指向上一棵树的左孩子，体现在代码中就是ls[x]=ls[last]
继续地递归且按照这种方式操作一直到叶子节点，这样我们就初步完成一颗最简单的主席树了。
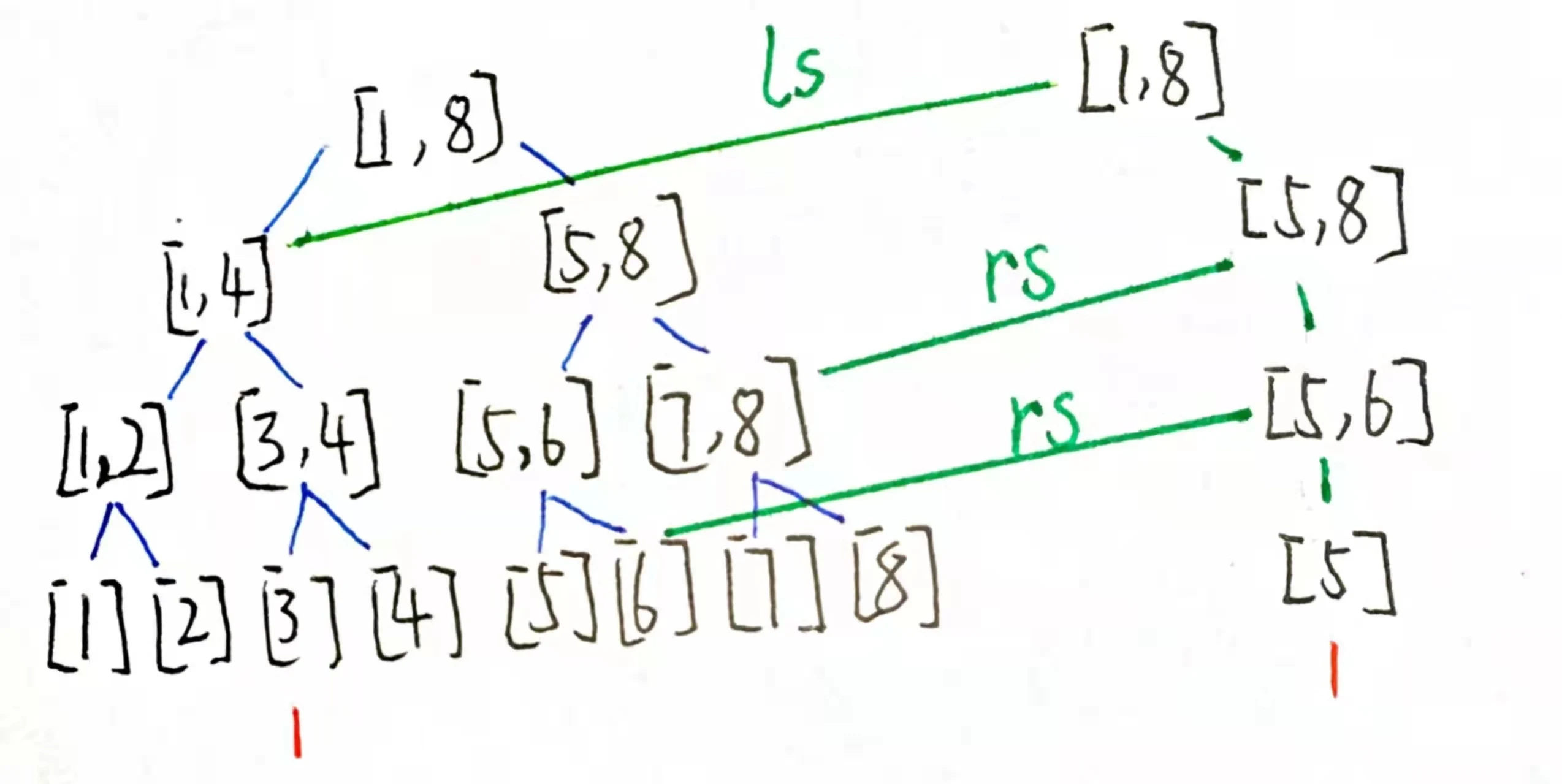
以接下来的节点为根的树要在前一棵树的基础上建。整颗主席树完成后就会是这个样子。
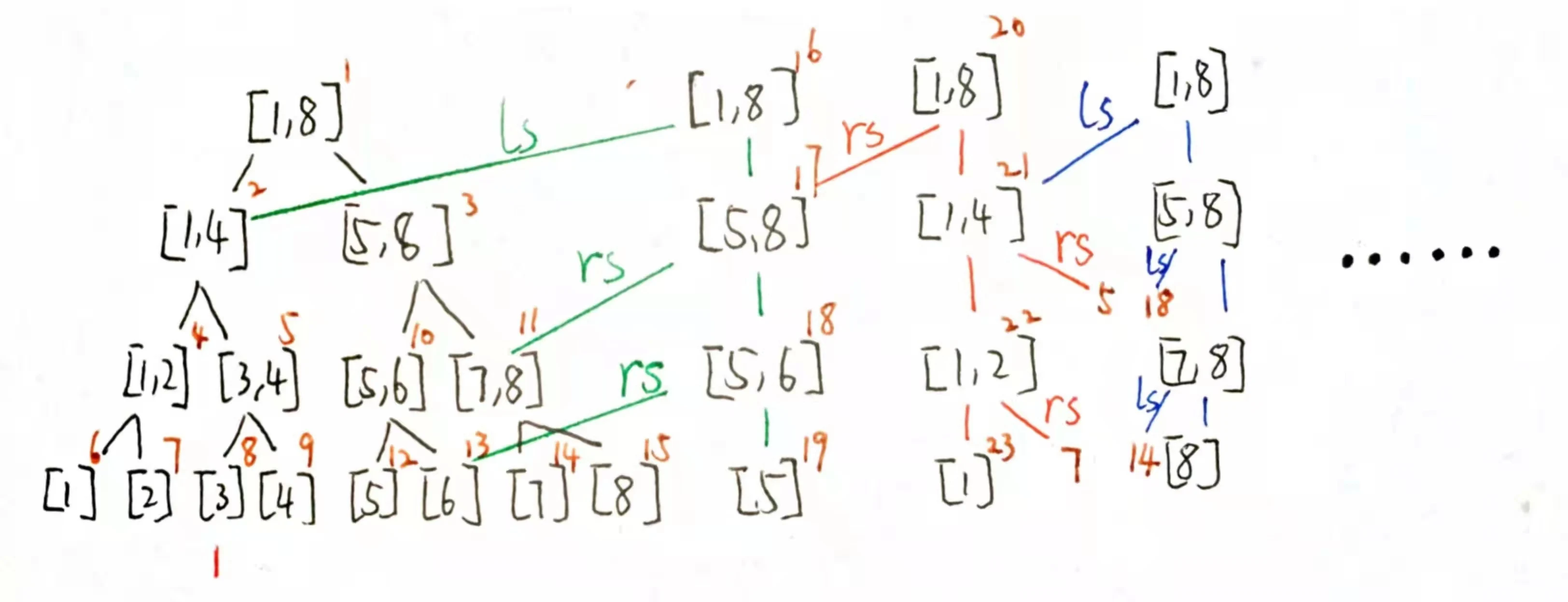
有了主席树，再结合前缀和的思想，我们就可以对区间第 \(k\) 小值进行求解。
比如现在要求区间内 [l,r] 的第 \(k\) 小，那么我们可以找到以 \(l-1\) 为根的树和以 \(r\) 为根的树，同时进行递归，用后者减去前者，得到的即为相应节点上，[l,r] 区间的值域线段树。
因为可持久化线段树不再是一棵完全二叉树，所以我们不能再用层次序编号，而是改为直接记录每个节点的左、右子节点编号。因为每次修改都会创建 \(O(\log N)\) 个新节点，所以可持久化线段树的空间复杂度为 \(O(N+M \log N)\)。为了节省空间，我们不再记录每个节点代表的区间 [l,r] 而是作为递归参数传递。
容易发现，可持久化线段树维护了每次操作之后线段树的历史形态。$ \forall i \in [1,M]$，
从 \(root[i]\) 出发向下能够访问到的节点就构成了执行完前 \(i\) 次修改操作时，维护初始序列的线段树。可持久化线段树的查询操作与一般线段树类似。
可持久化线段树难以支持大部分“区间修改”。当一个节点下传延迟标记时，一旦我们创建它左右子节点 \(lc,rc\) 的副本 \(lc',rc'\) 并把标记更新，那么所有依赖 \(lc,rc\) 的“线段树版本”都要改为依赖 \(lc',rc\)，甚至还要自底向上重新计算某些信息。这样的后果是灾难性的。在一些特殊的题目中，可以使用“标记永久化”代替标记的下传，但应用的局限性很大。
代码
namespace SegmentTree{
struct node{//左右孩子，区间和
int ls,rs,sum;
}t[M*50];//一共m次询问，每次最多新开2*logn个节点，所以空间复杂度是O(mlogn)
int tot=1,root[N]={1};//总结点个数,根节点编号
inline void Pushup(int x){
int &lx=t[x].ls,&rx=t[x].rs;
t[x].sum=t[lx].sum+t[rx].sum;
}
inline void update(int &x,int l,int r,int pos,int val,int now){
if(!x) x=++tot;
if(l==r){
t[x].sum=t[now].sum+val;
return;
}
int mid=(l+r)/2;
if(pos<=mid){
update(t[x].ls,l,mid,pos,val,t[now].ls);
t[x].rs=t[now].rs;
}
else{
t[x].ls=t[now].ls;
update(t[x].rs,mid+1,r,pos,val,t[now].rs);
}
Pushup(x);
}
inline int query(int x,int l,int r,int fr,int k){
if(!x) x=++tot;
if(l==r) return l;
int mid=(l+r)>>1;
if(t[t[x].ls].sum-t[t[fr].ls].sum>=k) return query(t[x].ls,l,mid,t[fr].ls,k);
else return query(t[x].rs,mid+1,r,t[fr].rs,k-t[t[x].ls].sum+t[t[fr].ls].sum);
}
}
