网络流初步
网络流是算法竞赛中的一个重要的模型,它分为两部分:网络和流。
网络,其实就是一张有向图,其上的边权称为容量。额外地,它拥有一个源点和汇点。
流,顾名思义,就像水流或电流,也具有它们的性质。如果把网络想象成一个自来水管道网络,那流就是其中流动的水。每条边上的流不能超过它的容量,并且对于除了源点和汇点外的所有点(即中继点),流入的流量都等于流出的流量。
一些概念
容量:每条边都有一个容量(水管的最大水流容量)
流量:每条边上的实际流经的水流大小
源点:出发点
汇点:结束点
可行流:一个合法解称作一个流,也就是一条可以从源点到汇点的一条合法路径。
弧流量限制条件: 0<=f(u,v)<=c(u,v)
平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外)
最大流:从源点S到汇点T的所有可行流之和。
-
网络流的性质
-
容量限制
-
斜对称性
-
流量平衡
除源汇点外,对于
-
最大流问题
网络流中最常见的问题就是网络最大流。
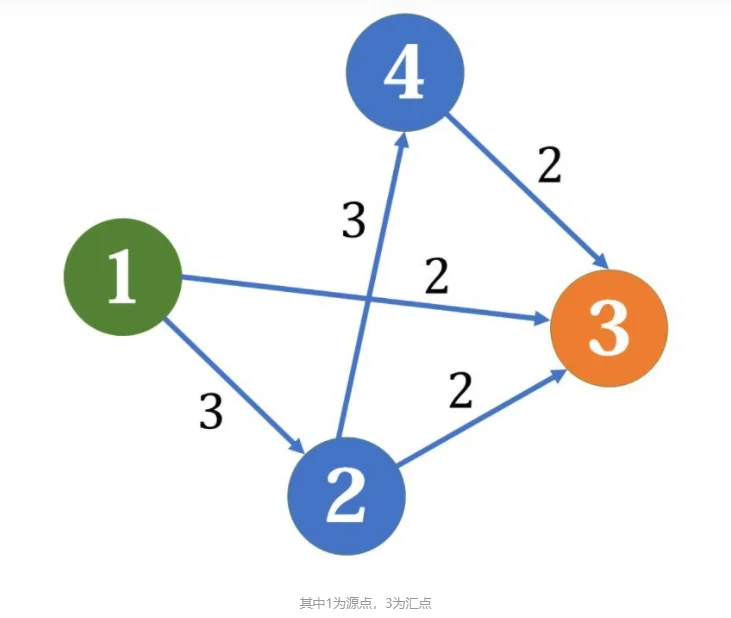
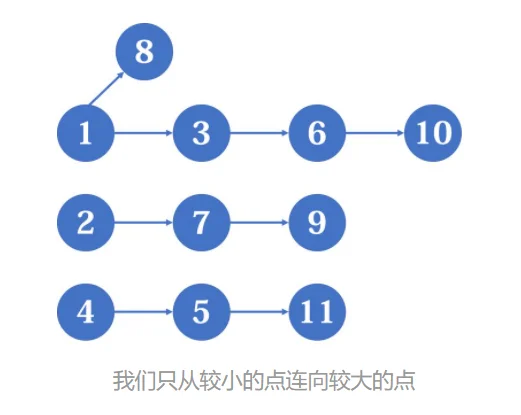
如下图所示,假设需要把一些物品从结点
下图展示了一种可能的方案,其中每条边中的第一个数字表示实际运送的物品数目,而第二个数字就是题目中的上限。
我们要做的就是求出从源点到汇点的最大流量是多少。
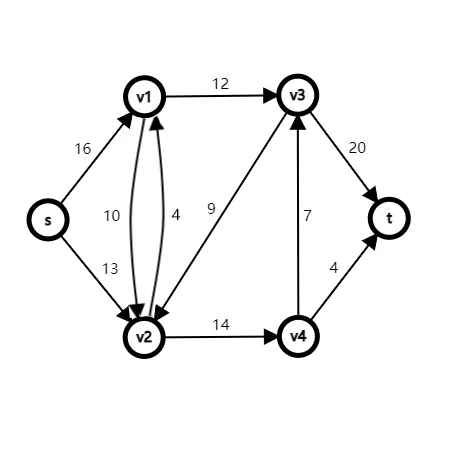
Ford-Fulkerson算法

-
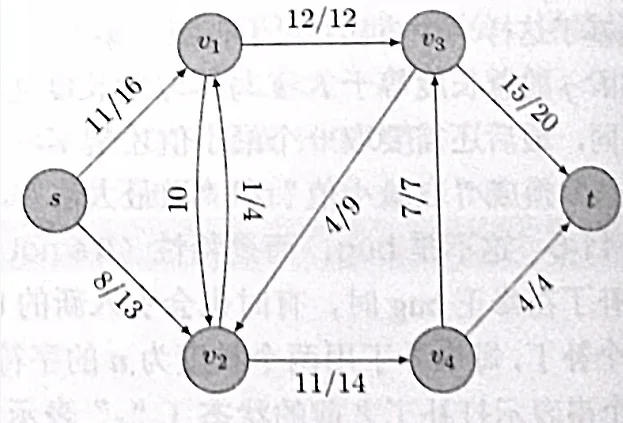
例如上图中我首先选择1->2->3,这是一条增广路,提供2流量;然后我们相应地扣除选择路径上各边的容量:
-
1->2的容量变成1
-
2->3的容量变成0
这时的容量称为残余容量。
-
-
然后我们再找到
-
增广路,是从源点到汇点的路径,其上所有边的残余容量均大于0。
-
FF算法就是不断寻找增广路,直到找不到为止。这个算法一定是正确的吗?好像不一定吧,比如这张图……
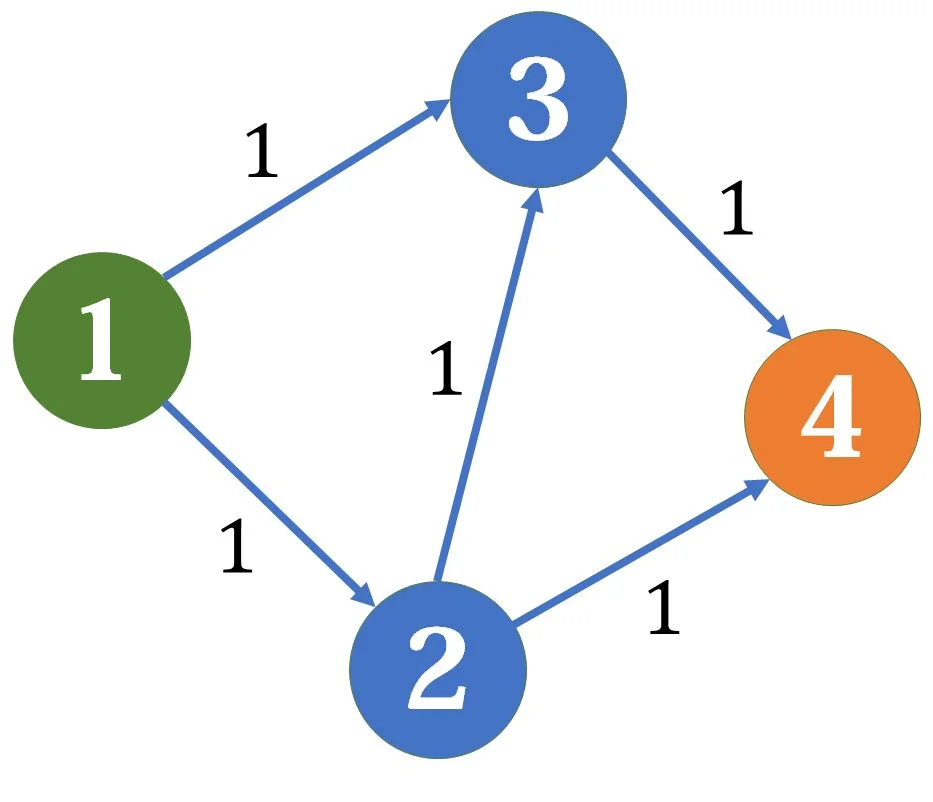
如果我们首先找到了1->2->3->4这条边,那么残余网络会变成这样:

现在已经找不到任何增广路了,最终求得最大流是1。但是,很明显,如果我们分别走1->3->4和1->2->4,是可以得到2的最大流的。
为了解决这个问题,我们引入反向边。在建边的同时,在反方向建一条边权为0的边:
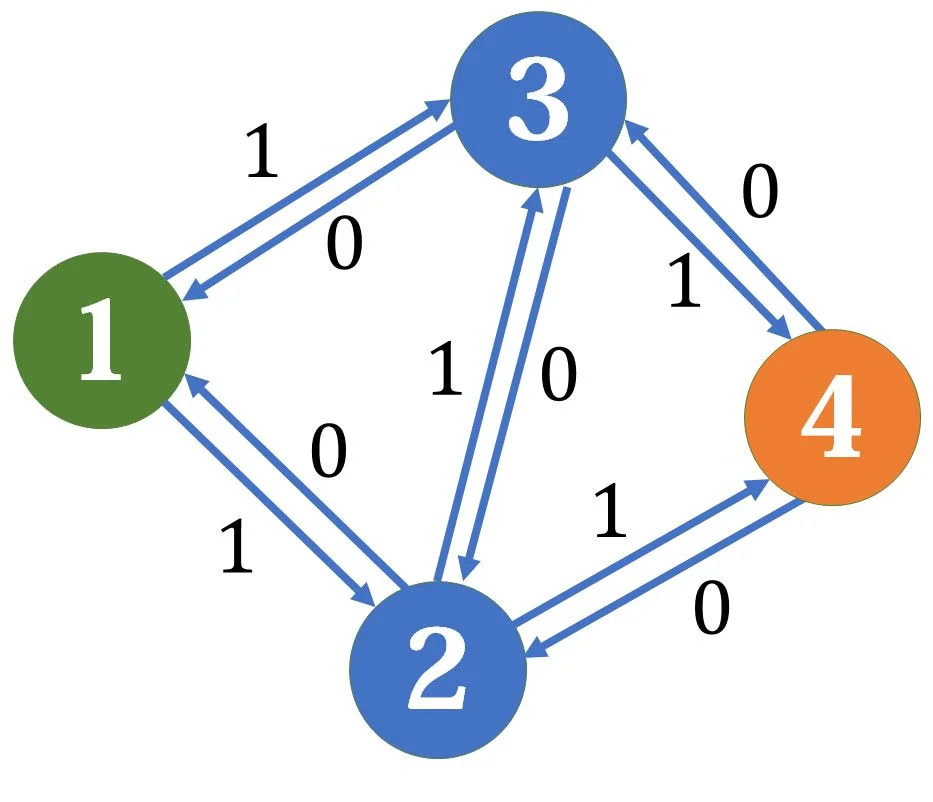
我们仍然选择
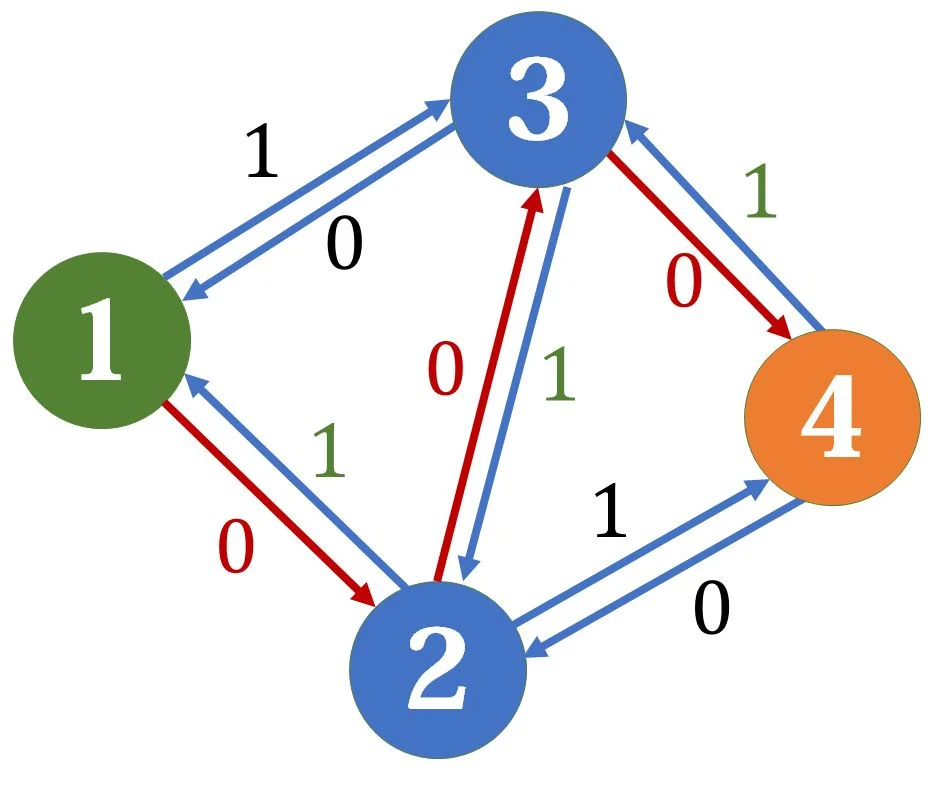
这时我们可以另外找到一条增广路:
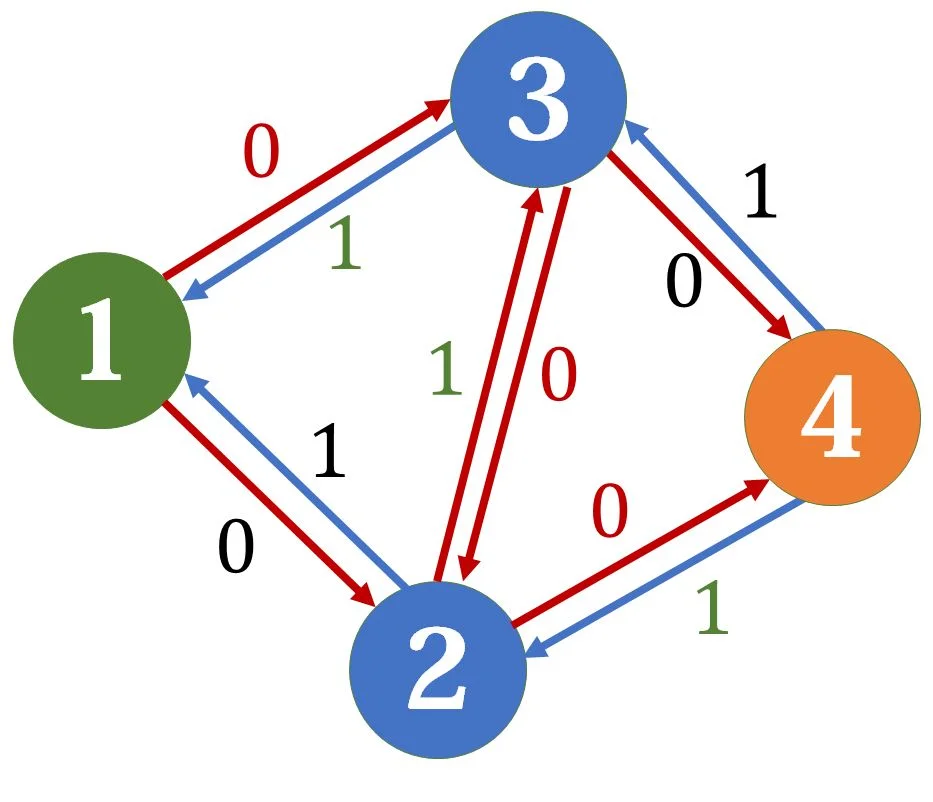
注意看,现在我们同时选择了
其实可以把反向边理解成一种撤销,走反向边就意味着撤回上次流经正向边的若干流量,这也合理解释了为什么扣除正向边容量时要给反向边加上相应的容量:反向边的容量意味着可以撤回的量。
加入了反向边这种反悔机制后,我们就可以保证,当找不到增广路的时候,流到汇点的流量就是最大流。
用
要注意,网络流算法的效率是玄学……虽然这个算法的复杂度上界非常高,但在随机图上表现也不算不可接受,至少可以通过洛谷模板题。当然,还有很多优化空间。
Edmond-Karp算法
其实,
为什么在这里BFS通常比DFS的效果好?因为DFS很可能会“绕远路”,而BFS可以保证每次找到的都是最短的增广路。它的复杂度上限是
Dinic算法
-
然而,最常用的网络流算法是Dinic算法。作为FF/EK算法的优化,它选择了先用BFS分层,再用DFS寻找。
-
它的时间复杂度上界是
-
我们可以使用多路增广节省很多花在重复路线上的时间:在某点DFS找到一条增广路后,如果还剩下多余的流量未用,继续在该点DFS尝试找到更多增广路。
-
此外还有当前弧优化。因为在Dinic算法中,一条边增广一次后就不会再次增广了,所以下次增广时不需要再考虑这条边。我们把head数组复制一份,但不断更新增广的起点。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int to[10010],val[10010],head[210],nxt[10010];
int deep[210],cur[210]//当前弧优化;
int cnt=1,ans,flag,s,t,n,m;
void add(int x,int y,int w) {
++cnt;
to[cnt]=y;
val[cnt]=w;
nxt[cnt]=head[x];
head[x]=cnt;
}
bool bfs() {
memset(deep,0,sizeof(deep));
deep[s]=0;
queue<int> q;
q.push(s);
while(q.size()) {
int h=q.front();
q.pop();
for(int i=head[h]; i; i=nxt[i]) {
int u=to[i];
if(deep[u]||u==s||!val[i]) continue;
deep[u]=deep[h]+1;
q.push(u);
if(u==t) return 1;
}
}
return 0;
}
int dfs(int x,int now) {
if(x==t) {
return now;
}
int res=0;
for(int &i=cur[x]; i; i=nxt[i]) {
int u=to[i];
if(val[i]==0||deep[u]<=deep[x]) continue;
res=dfs(u,min(val[i],now));
if(res==0) {
deep[u]=0;
continue;
}
val[i]-=res;
val[i^1]+=res;
return res;
}
return 0;
}
signed main() {
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1,p1,p2,p3; i<=m; i++) {
scanf("%lld%lld%lld",&p1,&p2,&p3);
add(p1,p2,p3);
add(p2,p1,0);
}
while(bfs()) {//bfs分层
for(int i=1;i<=n;i++) cur[i]=head[i];//当前弧优化
while(flag=dfs(s,INT_MAX)) ans+=flag;//dfs找增广路
}
cout<<ans;
return 0;
}
- 值得注意的是,这个算法如果用在二分图中复杂度是
最小费用最大流
我们现在来考虑比一般的网络流复杂一点的一个模型:最小费用最大流(Minimum Cost Maximum Flow,MCMF)。
现在网络上的每条边,除了容量外,还有一个属性:单位费用。一条边上的费用等于流量
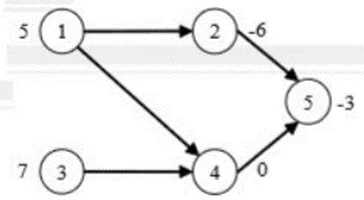
如下图,有多种方式可以达到最大流3,但是S->3->T (2) + S->3->2->T (1)这种流法的费用是

其实这个问题很好解决。我们已经知道,只要建了反向边,无论增广的顺序是怎样,都能求出最大流。所以我们只需要每次都增广费用最少的一条路径即可。具体地,把求最大流的算法里寻找增广路的部分用SPFA来实现(因为要费用最小,所以我们不能进行bfs分层操作):
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=310,M=20010,inf=0x3f3f3f3f3f3f3f3f;
int n,m,maxflow,mincost;
int head[N],nxt[M],to[M],flow[M],val[M],cnt=1;
int incf[N],pre[N],dis[N],vis[N];
//dis[i]:在增广路中到达节点 i 的路径单位费用之和
//incf[i]:在增广路中到达节点 i 时的路径最小容量
//pre[i]:在增广路中到达节点 i 的边的编号
void add(int x,int y,int z,int cost){
to[++cnt]=y;
flow[cnt]=z;
val[cnt]=cost;
nxt[cnt]=head[x];
head[x]=cnt;
}
bool SPFA(){
queue<int> q;
memset(dis,0x3f,sizeof(dis));
memset(vis,0,sizeof(vis));
incf[s]=0x3f3f3f3f;
dis[s]=0;
q.push(s);
while(q.size()){
int x=q.front();
q.pop();
vis[x]=0;
for(int i=head[x];i;i=nxt[i]){
int u=to[i];
if(flow[i]==0) continue;
if(dis[u]>dis[x]+val[i]){
dis[u]=dis[x]+val[i];
incf[u]=min(flow[i],incf[x]);
pre[u]=i;
if(!vis[u]){
vis[u]=1;
q.push(u);
}
}
}
}
if(dis[t]==inf) return 0;
return 1;
}
signed main() {
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1,p1,p2,p3,p4; i<=m; i++) {
scanf("%lld%lld%lld%lld",&p1,&p2,&p3,&p4);
add(p1,p2,p3,p4);
add(p2,p1,0,-p4);
}
while(SPFA()){
maxflow+=incf[t];
mincost+=incf[t]*dis[t];
int x=t;
while(x!=s){//在找增广路的过程中记录下用pre数组经过的边,正边减去流量,反边加上流量
flow[pre[x]]-=incf[t];
flow[pre[x]^1]+=incf[t];
x=to[pre[x]^1];
}
}
cout<<maxflow<<" "<<mincost;
return 0;
}
注意:建边的时候要这样建:
add(x, y, v, c);
add(y, x, 0, -c);
反向边的费用是正向边的相反数(反向边作为反悔机制必然是要退还给你之前走“冤枉路”的花费啊)
至于为什么用SPFA而不是Dijkstra,是因为费用流模型中因为反向边的存在,往往有负权边,而Dij一般不能在有负权边的图上跑。然而,众所周知,SPFA的复杂度不稳定,有时候会被卡,这时我们就需要用特殊处理后的Dijkstra网络流了(待补充)。
另外,求最大费用最大流我一直用的是边权全取反,跑MCMF,再把答案取反的做法,可能是我太蒻了qwq。
最小割
什么是割
对于一个网络流图
,割为一种点的划分方式:
将点划分为
和 两部分,其中源点 ,汇点
割的容量
为所有从 到 的边容量之和,即:
净流
表示穿过割 的流量之和,即:
以下图举例,虚线所示的割

结论:图的流f与割无关
根据网络流的定义,只有源点
任意非
最大流最小割定理
-
在所有可能的割中,存在一个容量最小的割
-
这个最小割限制了一个网络的流
-
设
- 残存网络
路径覆盖问题(最小割模型1)
路径覆盖问题又称最小覆盖集问题。

这里说的路径覆盖,是在DAG(有向无环图)上进行的,是指用找出尽可能少的一系列路径,使这些路径经过DAG上的所有点恰好各一次。
我们可以使用下面这样的思路:最开始,把每个点自己作为一条路径(这时一共有
但是,要如何保证覆盖数最少呢?我们可以使用网络流解决这个问题。
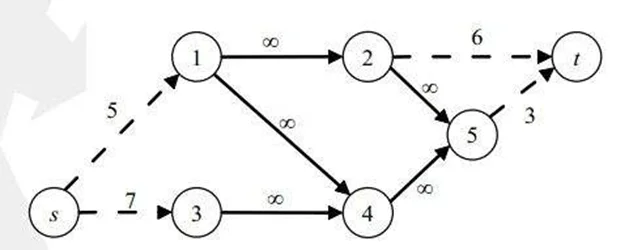
接下来,我们以这张DAG为例:

建网络流模型。我们把原图上的每个点拆成两个点(对于点x,可以把从它拆出去的点记为x+n),其中一个点与源点相连,另一个与汇点相连。

然后对于原DAG上的边A->B,我们在网络中连接上A->B':
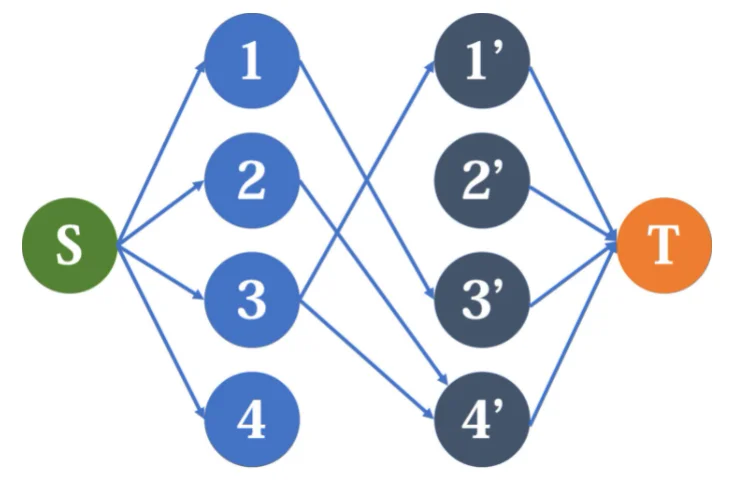
这里每一条边的容量均为1。现在我说:跑一遍最大流,便能得到最大合并路径数,再用点数去减即得最小路径覆盖数。这几乎是显然的:从
实际上,这里本质上就是二分图匹配,所以用匈牙利算法也是可以的,复杂度略差一点。
现在我们来写一道模板题:洛谷P2764 最小路径覆盖问题。题目内容就不贴了,和标题一样,就是求最小路径覆盖。但是这道题有个麻烦点在于,需要输出方案。
如何输出方案?一种思路是在跑完最大流后再DFS一遍,但那样未免麻烦,我们其实可以在增广途中就用一个数组succ[]记录每个点的下一个点。例如,如果使用Dinic算法,可以在dfs函数内部稍微加两句:
// ...
if (flow[i]>0 && deep[u]>deep[x]){
int res=dfs(u,min(flow[i],now));
if(!res){
deep[u]=0;
continue;
}
flow[i]-=res;
flow[i^1]+=res;
// 只有增广成功才修改nxt
succ[x]=u-n;// 如果选择用x+n记录从点x拆出的点,这里就这样写,记录下一个点
}
// ...
然后遍历起点,分别找到对应的路径输出:
for (int i=head[x];i;i=nxt[i]){
if (flow[i^1]) {
int u=to[i]-n;
while(u) printf("%d ", u), u=succ[u];
puts("");
}
}
这个遍历起点的方式可以注意一下。什么样的点是起点呢?如果
再来看一道例题:
这题乍一看跟网络流关系不大(好像也确实有其他做法),但如果我们把每根柱子看作一条路径,和为完全平方数的关系看作一条边的话,这完全就是DAG的路径覆盖问题了:
因为
这个题还有一个小坑点,拆点时不能拆成
最大权闭合子图(最小割模型2)
- 在一个有向无环图中,每个点有点权,现在需要选出一个子图,满足若一个点被选,它连向的所有点都被选,求子图的最大权值和是多少
- 建模方法
-
源点向所有正权点连边,容量为权值, 所有负权点向汇点连边,容量为权值的相反数,原图的边保留,权值为正无穷。
-
答案:选中的正权点-选中的负权点
=所有正权点-未选中的正权点-选中的负权点
=所有正权点-(未选中的正权点+选中的负权点)
=所有正权点-最小割=所有正权点-最大流
-
习题:Luogu P3410 拍照
上下界网络流
上下界网络流可以看做普通网络流的升级版,现在对于流量网络,我们不再只关注其流量的上界,而是同时关注流量的上下界。
无源汇有上下界可行流
这是上下界网络流中最简单的一种,给定一个没有源点和汇点、每条边的流量有上下界的流量网络,问是否存在一种可行流使得流量平衡。
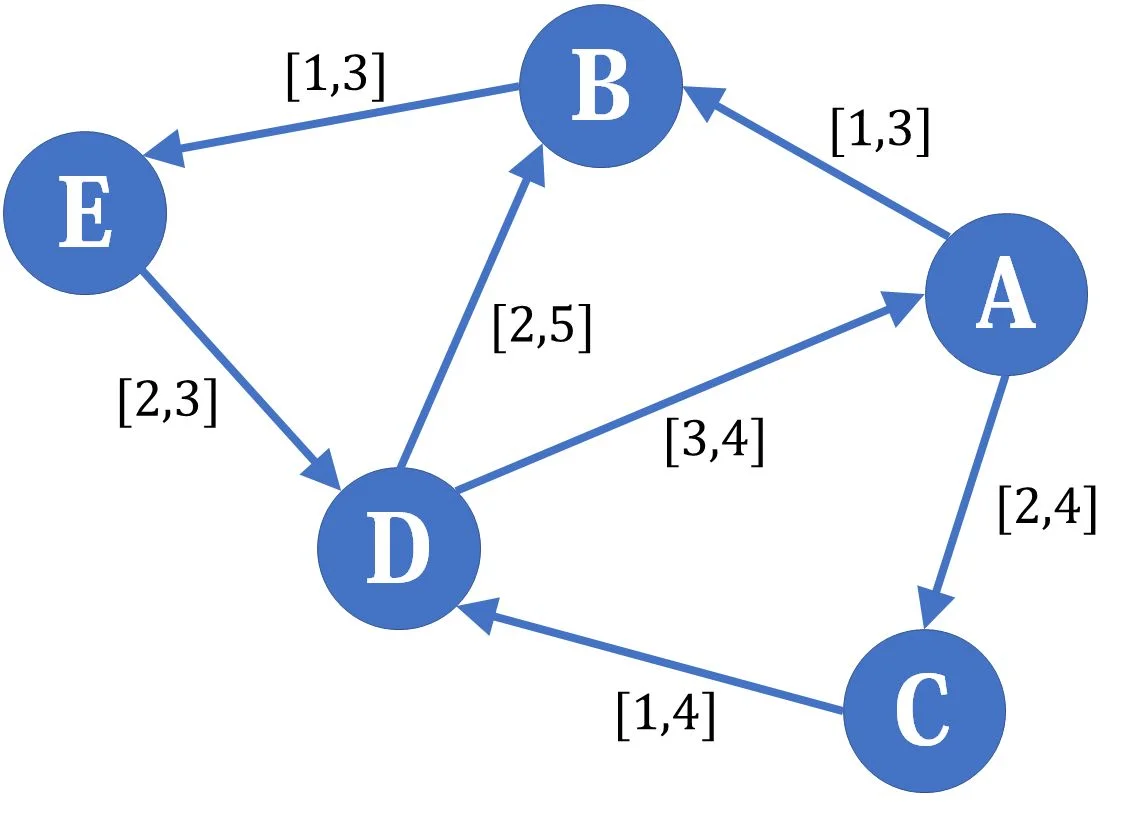
做法是,我们把它拆成两个结构与原图相同的普通网络,一个每条边的容量为原网络对应边的流量下界,另一个为对应边的流量上界与下界之差。
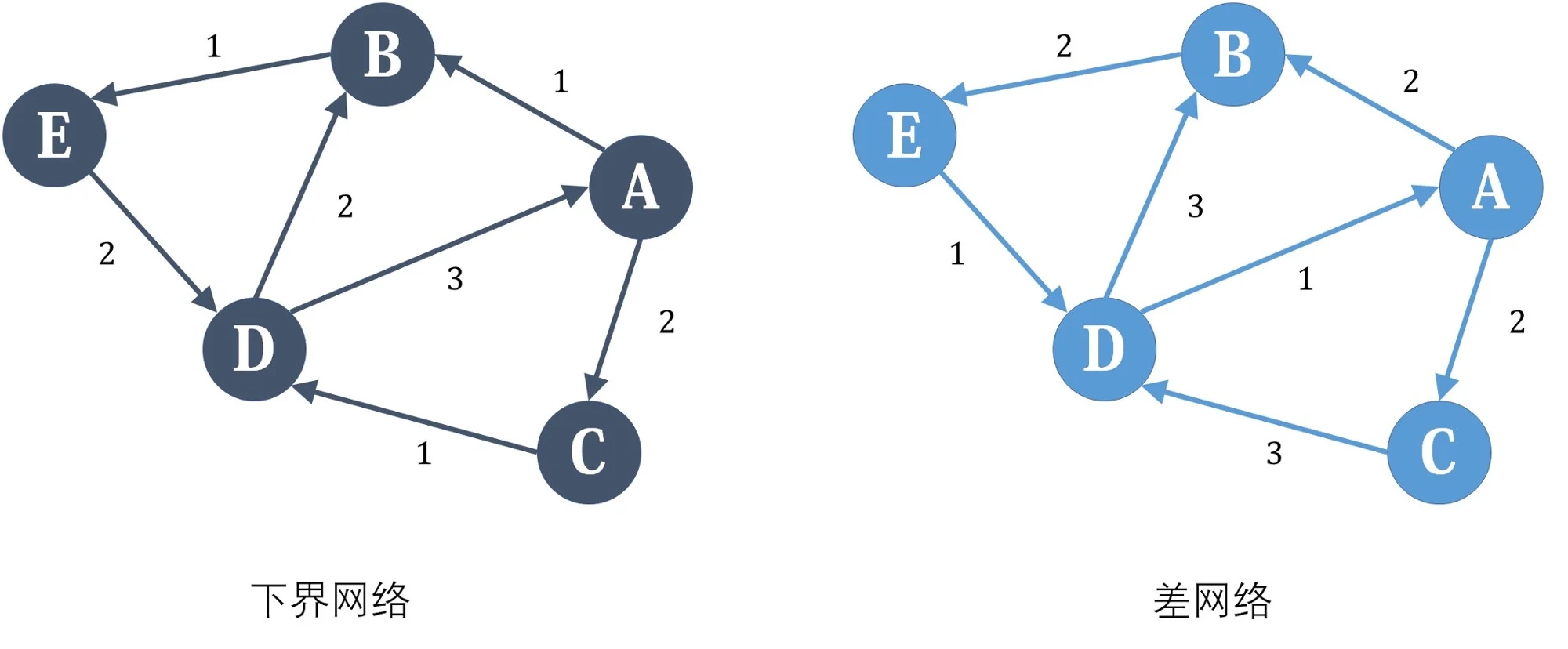
我们希望下界网络和差网络的流相加后恰好是原图的一个可行流,这首先要求下界网络是满流的(可行流必须达到每条边的下界)。但是下界网络满流后不一定流量平衡,所以我们要对差网络进行一定的修改以弥补这种不平衡。
我们分别考虑下界网络的每个点。A点,流入量为3,流出量也为3,所以是平衡的,那么在差网络中,也应该是平衡的,所以不做修改。B点,流入量为3,流出量为1,流入比流出多2,所以我们希望在差网络中,B的流出应该比流入多2,于是我们在差网络中新设一个源点,然后加入一条容量为2的附加边从源点连向B,这样在差网络平衡时,除去附加边,B点的流出恰好比流入多2,C点与B点类似。D点则相反,因为我们希望在差网络中D点流入比流出多2,所以我们新设一个汇点,然后从D点连一条容量为2的附加边到汇点,E点又和D类似。
也就是说,如果下界网络中某个点有
再直白一点就是下界网络差多少,就需要从差网络里流出多少,下界网络富裕的部分要流入差网络
这样,我们把差网络修改如下:
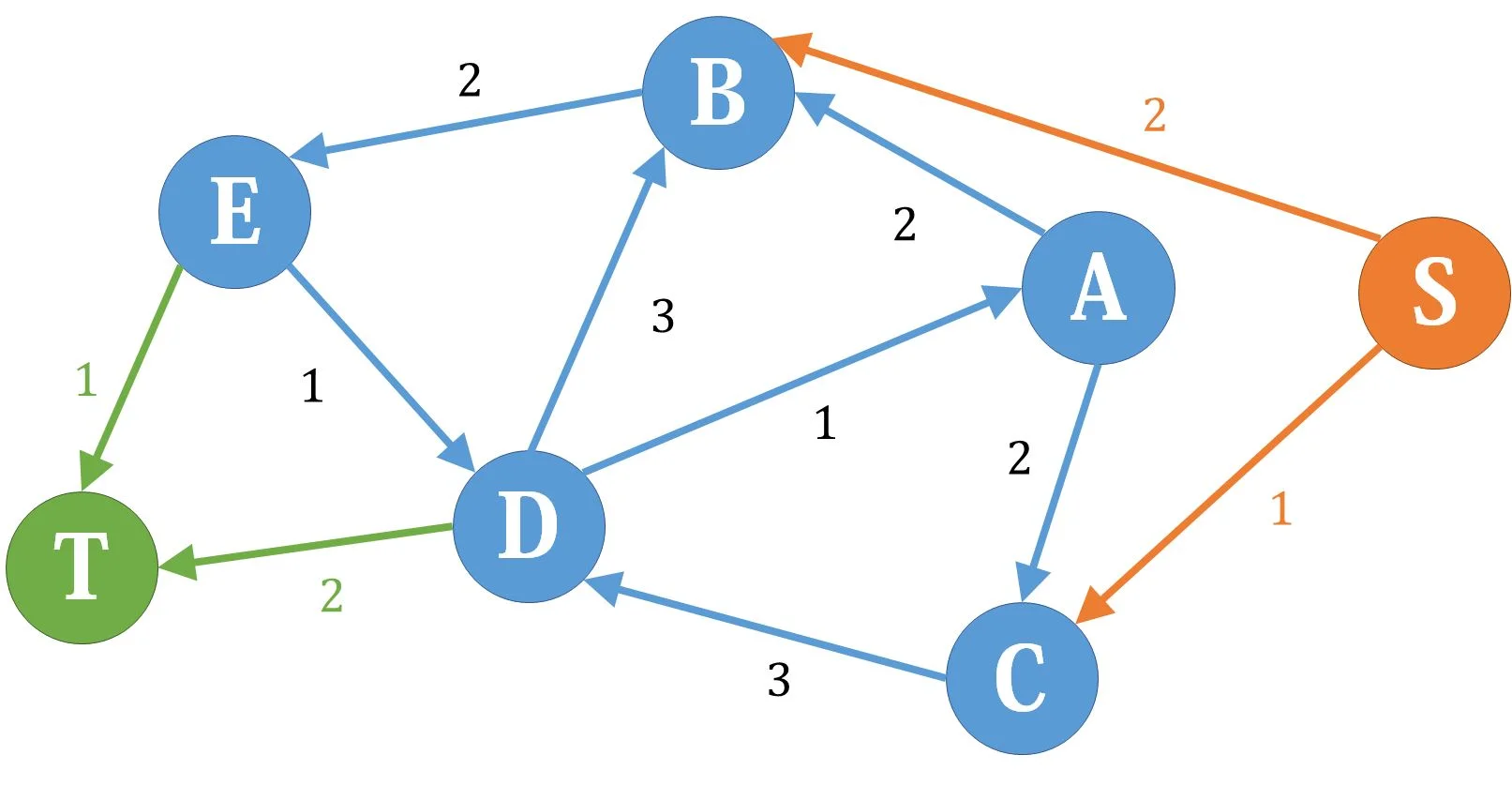
在差网络上跑一遍最大流,把每条非附加边的流,加上下界网络的满流,就是一个可行流。但是,如果跑完最大流发现,存在附加边未满流,那说明平衡条件没有得到满足,于是原图不存在可行流。
在实际中,是不需要建立下界网络的,只需要对差网络进行操作即可。另外最后判断的时候并无必要遍历所有附加边,而只需要判断所有从源点出发的边,或者判断所有连向汇点的边即可,因为根据网络流的性质,两者容量和应该相等,于是它们要么都满流,要么都不满流。
有源汇有上下界可行流
从汇点到源点连一条下界为
注意,这时候原来的源点和汇点已被处理成普通点,和之后差网络需要额外建立的源、汇点是不同的点,之后如果这两者同时出现,我们记前者为
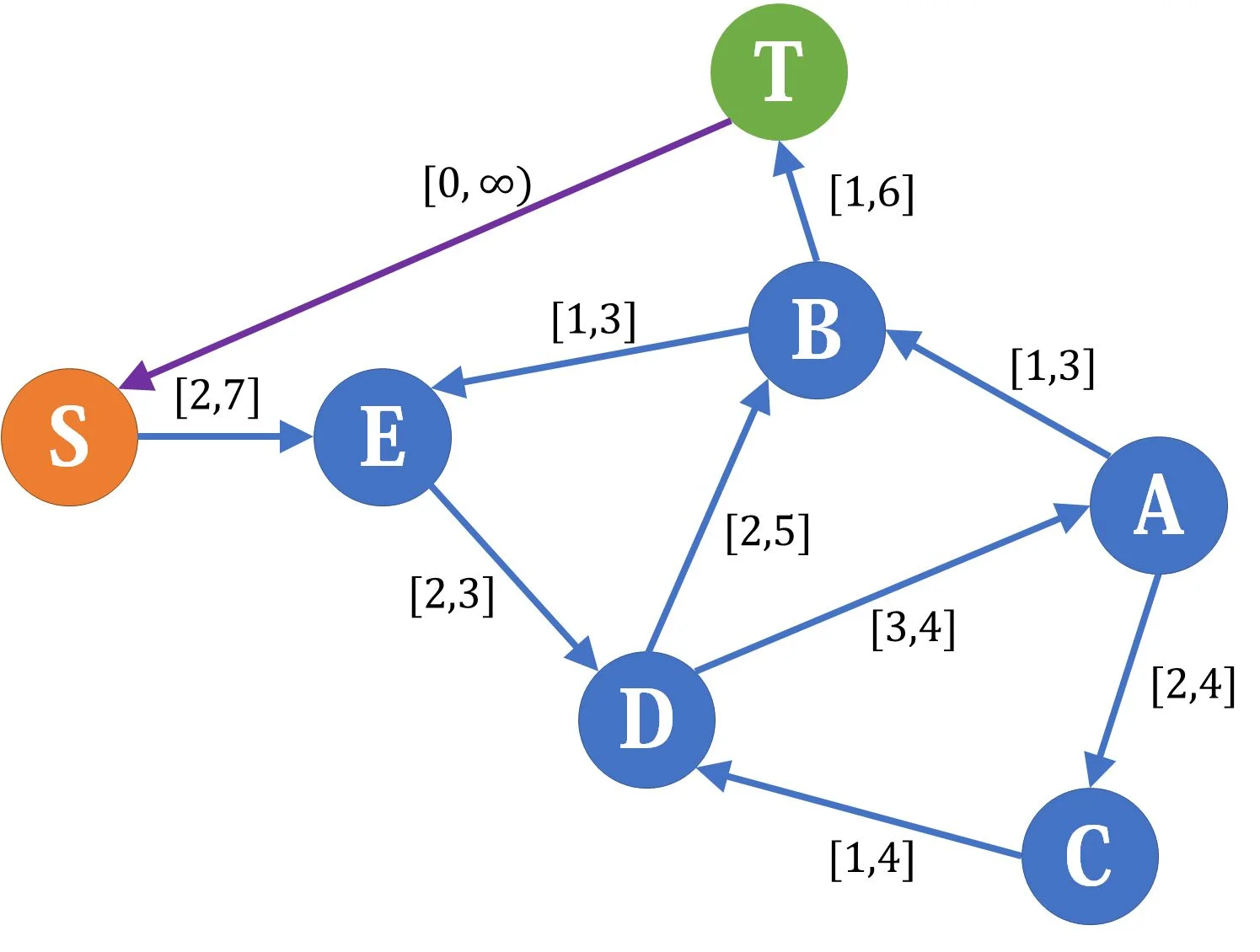
有源汇有上下界最大流
按照上一节的方法,我们已经得到了一个可行流,且知道它的流量就是

要求从
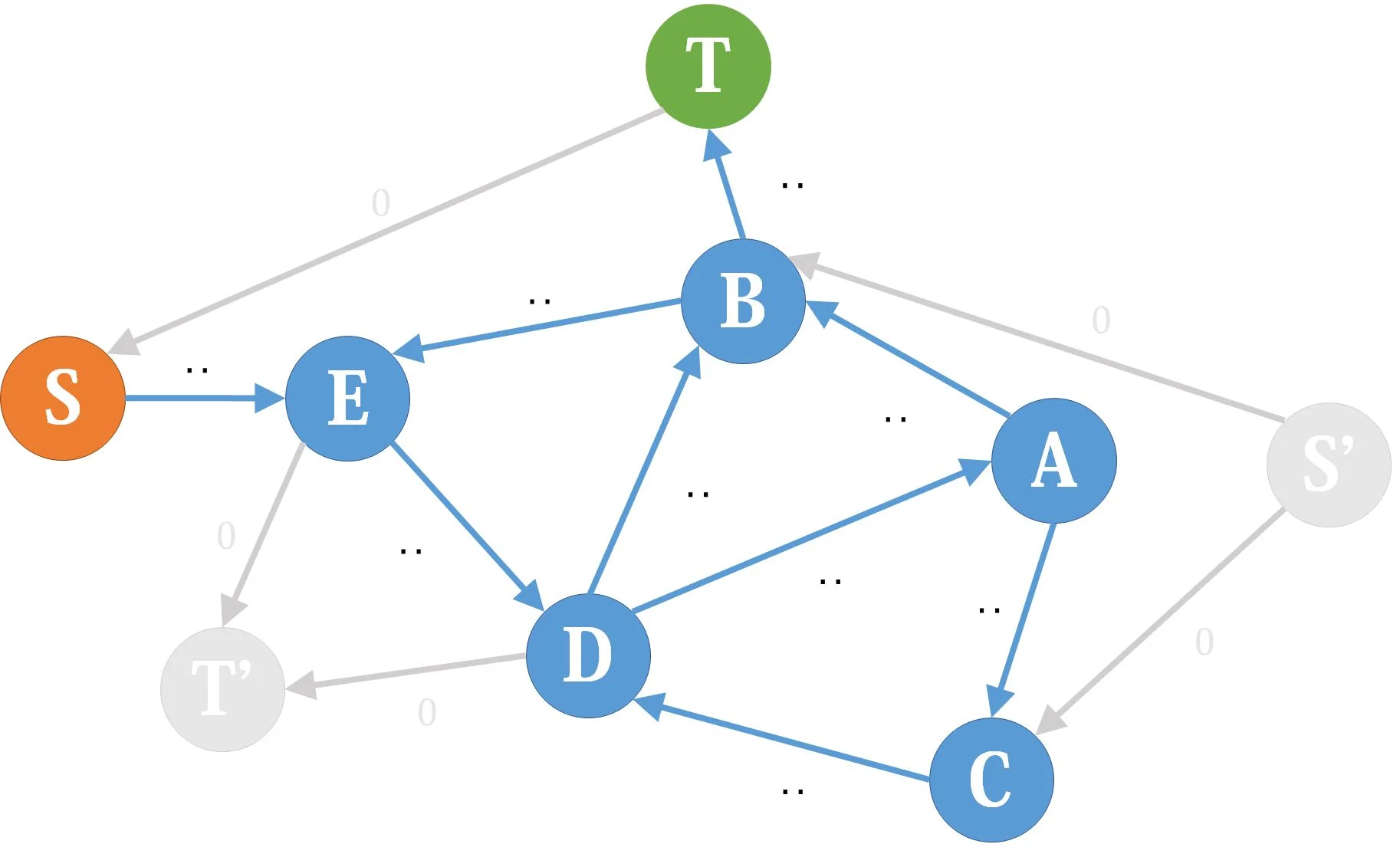
当然实际上
int in[MAXN], out[MAXN];
int main()
{
int s1, t1;
cin >> n >> m >> s1 >> t1; // 先把s,t当作普通点,用s1,t1存储
for (int i = 1; i <= m; ++i)
{
int from, to, lb, ub;
cin >> from >> to >> lb >> ub;
add(from, to, ub - lb);
add(to, from, 0);
in[to] += lb, out[from] += lb;
}
add(t1, s1, INF);
add(s1, t1, 0);
s = 300, t = 301;
for (int i = 1; i <= n; ++i)
{
if (in[i] > out[i])
{
add(s, i, in[i] - out[i]);
add(i, s, 0);
}
else if (in[i] < out[i])
{
add(i, t, out[i] - in[i]);
add(t, i, 0);
}
}
dinic();
for (int e = head[s]; e; e = edges[e].next)
if (edges[e].w != 0)
{
cout << "please go home to sleep" << endl;
return 0;
}
s = s1, t = t1; // 切换源汇点
int flow = 0;
for (int e = head[t]; e; e = edges[e].next)
if (edges[e].to == s)
{
flow = edges[e ^ 1].w;
edges[e].w = edges[e ^ 1].w = 0; // 删除源汇点间的附加边
}
cout << dinic() + flow << endl;
return 0;
}
有源汇有上下界最小流
跟上面几乎完全相同,只需要在拆掉附加边后,从汇点到源点,而不是从源点到汇点跑一遍最大流。可行流的流量,减去从汇点到源点的最大流即为答案。如果说上下界最大流是把残量网络“榨干”,那么上下界最小流就是把不需要的流“退回”。
以 Luogu P4843 清理雪道 为例
#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 50010, inf = 0x3f3f3f3f;
int n, Max, del;
int head[N], nxt[M], to[M], flow[M], cnt = 1;
int deep[510], cur[N], flag;
int in[N];
int ans = 0, s, t, tt, ss;
void add(int x,int y,int z){
to[++cnt] = y;
flow[cnt] = z;
nxt[cnt] = head[x];
head[x] = cnt;
}
bool bfs() {
memset(deep,0,sizeof(deep));
deep[ss] = 1;
queue<int> q;
q.push(ss);
while(q.size()) {
int h = q.front();
q.pop();
for(int i = head[h]; i; i = nxt[i]) {
int u = to[i];
if(deep[u] || !flow[i]) continue;
deep[u] = deep[h] + 1;
q.push(u);
if(u == tt) return 1;
}
}
return 0;
}
int dfs(int x,int now) {
if(x == tt) {
return now;
}
int res = 0;
for(int &i = cur[x]; i; i = nxt[i]) {
int u = to[i];
if(flow[i] == 0 || deep[u] <= deep[x]) continue;
res = dfs(u, min(flow[i], now));
if(res == 0) {
deep[u] = 0;
continue;
}
flow[i] -= res;
flow[i^1] += res;
return res;
}
return 0;
}
int main(){
cin >> n;
s = n + 1, t = n + 2, ss = n + 3, tt = n + 4;
//s:源 t:汇 ss:超级源 tt:超级汇
for(int i = 1, k; i <= n; i++){
cin >> k;
for(int j = 1, b; j <= k; j++){
cin >> b;
add(i, b, inf);
add(b, i, 0);
in[b]++;
in[i]--;
}
add(s, i, inf);
add(i, s, 0);
add(i, t, inf);
add(t, i, 0);
}
//汇点向源点建边
add(t, s, inf);
del = cnt;
add(s, t, 0);
for(int i = 1; i <= n; i++){//超级源点和超级汇点的建边操作
if(in[i] > 0){
add(ss, i, in[i]);
add(i, ss, 0);
}
else if(in[i] < 0){
add(i, tt, -in[i]);
add(tt, i, 0);
}
}
while(bfs()){
for(int i = 1; i <= n + 4; i++) cur[i] = head[i];
while(flag = dfs(ss,inf)){}
}
Max = flow[del^1];
flow[del] = flow[del^1] = 0;
//从汇点向源点跑最大流,退回多余的流量
//这里为了方便直接重定义ss和tt
ss = t;
tt = s;
while(bfs()){
for(int i = 1; i <= n + 4; i++) cur[i] = head[i];
while(flag = dfs(ss,inf)){
ans += flag;
}
}
cout << Max-ans;
return 0;
}
有上下界最小费用可行流
和(无/有源汇)有上下界可行流的原理相同,也是拆成两个网络。所有附加边的费用设为0。最后的费用是下界网络满流的费用,加上在差网络上跑MCMF后得到的费用之和。而前者即所有边的容量与费用乘积的和。注意,这样求出来的是满足最小费用的可行流,而不是满足流最大的前提下费用最小的流。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!