随机化算法
所有随机化算法的核心都是 概率 \(\times\) 正确率 能够近似正解从而优雅骗分
随机化贪心
贪心，是一个很好的算法，只可惜适用的范围不广。随机化，是一个很好的算法，只可惜正确率不高。
如果将这两个算法结合起来，我们能不能得到一个适用范围广、正确率较高的算法呢？
答案是肯定的。
随机化贪心，顾名思义，就是边随机边贪心
这类算法适合解决动态规划类的题目
思想：在贪心原则正确的情况下，随机执行足够多次，就是正解了(涉及到概率学，这里不深究)
不要以为随机到正解几率很小，假设随机到正解的概率为0.1%，我们执行100000次贪心，每次取最优，得到正解的概率是100%
也就是这种贪心也变成了某种意义上的正解
在说随机化贪心前先说一下随机数据生成
随机数据生成
头文件ctime,cstdlib
调用函数 rand(),srand()，其中注意windows中RAND_MAX=32767。
rand()返回0~RAND_MAX之间随机整数。
srand()初始化rand()种子。
random_shuffle()用来对一个元素序列进行重新排序（随机的）
时间函数
我们希望我们的答案是正确的，我们就要多跑几遍贪心，但我们同时又要保证不超时，如果我们能知道程序运行的时间，并及时停止就能在保证算法正确率的同时又不会超时。
我们可以通过时间函数来调取程序运行的时间：
#define timeused ((double)clock()/CLOCKS_PER_SEC)
double beg=timeused;
while(timeused-beg<0.95){
……
}
至于例子嘛……
例题
题目描述
参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 \(n\) 个深埋在地下的宝藏屋， 也给出了这 \(n\) 个宝藏屋之间可供开发的 \(m\) 条道路和它们的长度。
小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。
小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。
在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以 任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。
新开发一条道路的代价是 \(\mathrm{L} \times \mathrm{K}\)。其中 \(L\) 代表这条道路的长度，\(K\) 代表从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋） 。
请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代价最小，并输出这个最小值。
输入格式
第一行两个用空格分离的正整数 \(n,m\)，代表宝藏屋的个数和道路数。
接下来 \(m\) 行，每行三个用空格分离的正整数，分别是由一条道路连接的两个宝藏屋的编号（编号为 \(1-n\)），和这条道路的长度 \(v\)。
输出格式
一个正整数，表示最小的总代价。
样例 #1
样例输入 #1
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 1
样例输出 #1
4
样例 #2
样例输入 #2
4 5
1 2 1
1 3 3
1 4 1
2 3 4
3 4 2
样例输出 #2
5
提示
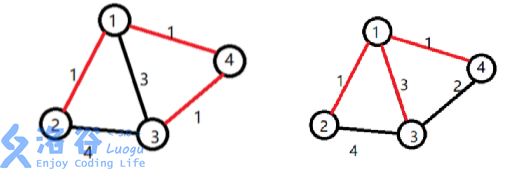
【样例解释 \(1\)】
小明选定让赞助商打通了 \(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\)，挖掘了 \(2\) 号宝藏。开发了道路 \(1 \to 4\)，挖掘了 \(4\) 号宝藏。还开发了道路 \(4 \to 3\)，挖掘了 \(3\) 号宝藏。
工程总代价为 $1 \times 1 + 1 \times 1 + 1 \times 2 = 4 $。
【样例解释 \(2\)】
小明选定让赞助商打通了 \(1\) 号宝藏屋。小明开发了道路 \(1 \to 2\)，挖掘了 \(2\) 号宝藏。开发了道路 \(1 \to 3\)，挖掘了 \(3\) 号宝藏。还开发了道路 \(1 \to 4\)，挖掘了 \(4\) 号宝藏。
工程总代价为 \(1 \times 1 + 3 \times 1 + 1 \times 1 = 5\)。
【数据规模与约定】
对于 $ 20%$ 的数据： 保证输入是一棵树，\(1 \le n \le 8\)，\(v \le 5\times 10^3\) 且所有的 \(v\) 都相等。
对于 \(40\%\) 的数据： \(1 \le n \le 8\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^3\) 且所有的 \(v\) 都相等。
对于 $ 70%$ 的数据： \(1 \le n \le 8\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^3\)。
对于 $ 100%$ 的数据： \(1 \le n \le 12\)，\(0 \le m \le 10^3\)，\(v \le 5\times 10^5\)。
思路
题意简单来说就是给定一个 \(n\) 个点 \(m\) 条边的图，请你求出一个有根树。
满足每个点的深度和它到父节点的边权乘积之和最小。
可以利用random_shuffle()将打通宝藏屋的顺序随机出来，然后贪心求解即可。
即 假如要打通第 \(i\) 个宝藏屋，那么从已打通的宝藏屋中选出打通道路花费最小的即可。
#include<bits/stdc++.h>
#define timeused ((double)clock()/CLOCKS_PER_SEC)
#define ll long long
using namespace std;
int a[20][20],n,m;
int ans=0x3f3f3f3f,now;
int f[20];
int dep[20];
void tx(){
now=0;
memset(dep,0,sizeof(dep));
dep[f[1]]=1;//记录深度
for(int i=2;i<=n;++i){
int t=f[i];
int mv=0x3f3f3f3f,mp=0;
for(int j=1;j<=n;++j){
if(!dep[j]||a[j][t]==-1) continue;
if(mv>a[j][t]*dep[j]) mv=a[j][t]*dep[j],mp=j;
}
if(!mp) goto wrong;//因为是随机的顺序可能无法找到，此时退出
dep[t]=dep[mp]+1;
now+=mv;
}
ans=min(ans,now);
wrong:
return;
}
int main() {
for(int j=0;j<20;j++)//初始化a[i][j]=-1
for(int i=0;i<20;i++){
a[i][j]=-1;
}
cin>>n>>m;
for(int i=1,x,y,w;i<=m;i++){//邻接矩阵存图
cin>>x>>y>>w;
if(a[x][y]>w||a[x][y]==-1){
//两个宝藏间如果有多条路取最小的or第一次出现这两个宝藏间的路
a[x][y]=w;
a[y][x]=w;
}
}
double beg=timeused;
for(int i=1;i<=n;i++) f[i]=i;
while(timeused-beg<0.95){
random_shuffle(f+1,f+n+1);//随机一个找宝藏的顺序
tx();//对于当前的顺序求最小花费
}
cout<<ans;
}
模拟退火
什么是退火？（选自百度百科）
退火是一种金属热处理工艺，指的是将金属缓慢加热到一定温度，保持足够时间，然后以适宜速度冷却。如果快速降温，很容易使得温度不均匀而没法达成全局最低温，而退火是稳中求进，使分子间内能减少，最终温度降到最低
什么是模拟退火
模拟退火就是仿照金属退火的形式而研发的一种随机化算法。
介绍模拟退火前，还是有必要先介绍爬山算法。
爬山算法
爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。
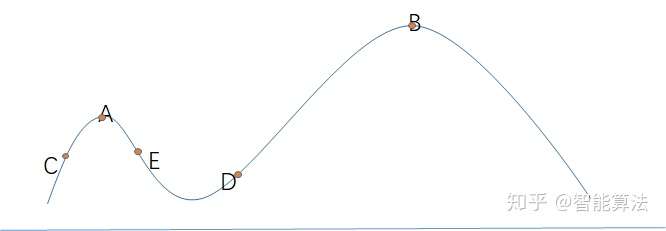
爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如上图所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。
模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。如下图：
随着温度的降低，跳跃越来越不随机，最优解也越来越稳定。
这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来。将温度 \(T\) 当作控制参数，目标函数值 \(f\) 视为内能 \(E\)，而固体在某温度 \(T\) 时的一个状态对应一个解，然后算法试图随着控制参数 \(T\) 的降低，使目标函数 \(f\)(内能\(E\))也逐渐降低，直至趋于全局最小值（退火中低温时的最低能量状态），就像金属退火过程一样。
关于爬山算法与模拟退火，有一个有趣的比喻：
-
爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。
-
模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
当一个问题的方案数量极大（甚至是无穷的）而且不是一个单峰函数时，常使用模拟退火求解。
模拟退火——优雅的骗分
实现
先用一句话概括：如果新状态的解更优则修改答案，否则以一定概率接受新状态。
我们定义当前温度为 \(T\)，新状态与已知状态（由已知状态通过随机的方式得到）之间的能量（值）差为 \(\Delta E(\Delta E \ge 0 )\)，则发生状态转移（修改最优解）的概率为
注意：我们有时为了使得到的解更有质量，会在模拟退火结束后，以当前温度在得到的解附近多次随机状态，尝试得到更优的解（其过程与模拟退火相似）。
模拟退火时有三个参数：初始温度 \(T_0\)，降温系数 \(d\)，终止温度 \(T_k\)。
\(T_0\) 是一个比较大的数，\(d\) 是一个非常接近 \(1\) 但是小于 \(1\) 的数，\(T_k\) 是一个接近 \(0\) 的正数。
首先让温度 \(T=T_0\)，然后按照上述步骤进行一次转移尝试，再让 \(T=T * d\) 。当 \(T<T_k\) 时模拟退火过程结束，当前最优解即为最终的最优解。
注意为了使得解更为精确，我们通常不直接取当前解作为答案，而是在退火过程中维护遇到的所有解的最优值。
代码
此处代码以 「BZOJ 3680」吊打 XXX（求 个 \(n\) 点的带权类费马点）为例。
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <ctime>
const int N = 10005;
int n, x[N], y[N], w[N];
double ansx, ansy, dis;
double Rand() { return (double)rand() / RAND_MAX; }
double calc(double xx, double yy) {
double res = 0;
for (int i = 1; i <= n; ++i) {
double dx = x[i] - xx, dy = y[i] - yy;
res += sqrt(dx * dx + dy * dy) * w[i];
}
if (res < dis) dis = res, ansx = xx, ansy = yy;
return res;
}
void simulateAnneal() {
double t = 100000;
double nowx = ansx, nowy = ansy;
while (t > 0.001) {
double nxtx = nowx + t * (Rand() * 2 - 1);
double nxty = nowy + t * (Rand() * 2 - 1);
double delta = calc(nxtx, nxty) - calc(nowx, nowy);
if (exp(-delta / t) > Rand()) nowx = nxtx, nowy = nxty;
t *= 0.97;
}
for (int i = 1; i <= 1000; ++i) {
double nxtx = ansx + t * (Rand() * 2 - 1);
double nxty = ansy + t * (Rand() * 2 - 1);
calc(nxtx, nxty);
}
}
int main() {
srand(time(0));
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d%d", &x[i], &y[i], &w[i]);
ansx += x[i], ansy += y[i];
}
ansx /= n, ansy /= n, dis = calc(ansx, ansy);
simulateAnneal();
printf("%.3lf %.3lf\n", ansx, ansy);
return 0;
}
一些技巧
分块模拟退火
有时函数的峰很多，模拟退火难以跑出最优解。
此时可以把整个值域分成几段，每段跑一遍模拟退火，然后再取最优解。
