Manacher
Manacher算法是一个用来查找一个字符串中的最长回文子串(不是最长回文序列)的线性算法。它的优点就是把时间复杂度为
暴力匹配
暴力匹配算法的原理很简单,就是 从原字符串的首部开始,依次向尾部进行遍历,每访问一个字符,就以此字符为中心向两边扩展,记录该点的最长回文长度。 那么我们可以想想,这样做存在什么弊端,是不是可以求出真正的最长回文子串?
答案是显然不行的,我们从两个角度来分析这个算法
1.不适用于偶数回文串
我们举两个字符串做例子,它们分别是 "aba","abba",我们通过肉眼可以观察出,它们对应的最长回文子串长度分别是3和4,然而我们要是用暴力匹配的方法去对这两个字符串进行操作就会发现,"aba" 对应的最长回文长是 "131","abba" 对应的最长回文长度是 "1111",我们对奇数回文串求出了正确答案,但是在偶数回文串上并没有得到我们想要的结果,通过多次测试我们发现,这种暴力匹配的方法不适用于偶数回文串
2.时间复杂度
这里的时间复杂度是一个平均时间复杂度,并不代表每一个字符串都是这个复杂度,但因为每到一个新位置就需要向两边扩展比对,所以平均下来时间复杂度达到了
Manacher算法本质上也是基于暴力匹配的方法,只不过做了一点简单的预处理,且在扩展时提供了加速
Manacher对字符串的预处理
我们知道暴力匹配是无法解决偶数回文串的,可Manacher算法也是一种基于暴力匹配的算法,那它是怎么来实现暴力匹配且又不出错的呢?它用来应对偶数字符串的方法就是——做出预处理,这个预处理可以巧妙的让所有字符串都变为奇数回文串,不论它原本是什么。操作实现也很简单,就是将原字符串的首部和尾部以及每两个字符之间插入一个特殊字符,这个字符是什么不重要,不会影响最终的结果(具体原因会在后面说),这一步预处理操作后的效果就是原字符串的长度从
这里解释一下为什么预处理后不会影响对字符串的扩展匹配
比如我们的原字符串是 "aa" ,假设预处理后的字符串是 "#a#a#" ,我们在任意一个点,比如字符 '#' ,向两端匹配只会出现 'a' 匹配 'a' , '#' 匹配 '#' 的情况,不会出现原字符串字符与特殊字符匹配的情况,这样就能保证我们不会改变原字符串的匹配规则。通过这个例子,你也可以发现实际得到的结果与上述符合。
Manacher算法核心
Manacher算法的核心部分在于它巧妙的令人惊叹的加速,这个加速一下把时间复杂度提升到了线性,让我们从暴力的算法中解脱出来,我们先引入概念,再说流程,最后提供实现代码。
概念:
ManacherString:经过Manacher预处理的字符串,以下的概念都是
基于Manacher产生的。
回文半径和回文直径:因为处理后回文字符串的长度一定是奇数,所以回文半径是包括回文中心在内的回文子串的一半的长度,回文直径则是回文半径的2倍减1。比如对于字符串 "aba",在字符 'b' 处的回文半径就是2,回文直径就是3。
最右回文边界
回文中心
半径数组:这个数组记录了原字符串中每一个字符对应的最长回文半径。
流程:
-
步骤1:预处理原字符串
先对原字符串
-
步骤2:
-
步骤3:开始从下标
-
分支1:
-
分支2:
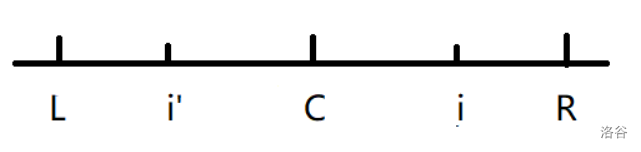
-
情况1:
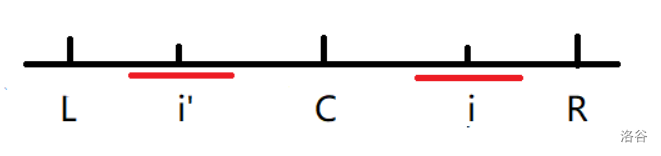
红线部分是
-
情况2:
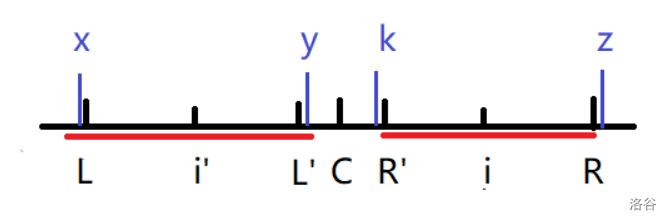
首先我们设
-
情况3:

因为
-
-
总结一下,Manacher算法的具体流程就是先匹配 -> 通过判断
时间复杂度:
我们可以计算出时间复杂度为何是线性的,分支一的情况下时间时间复杂度是
代码实现
整个代码并不是对上述流程的生搬硬套(那样会显得代码冗长),代码进行了精简优化
#include <bits/stdc++.h>
using namespace std;
const int N=2.2e7+10;
int n,R,C;
int b[N],ans;//b:半径数组
char a[N],s[N];
void init(){//预处理出新的字符串
a[0]='~',a[n=1]='#';//新字符串下标从 1 开始,a[0]设为其他字符防止越界
for(int i=0;i<strlen(s);i++)
a[++n]=s[i],a[++n]='#';
}
int main() {
cin>>s;//输入原字符串
init();
for(int i=1;i<=n;i++){
if(i<=R) //对于分支2的三种情况,i的回文半径至少是 i'的回文半径 和 i到R的距离 二者中较小的一个
b[i]=min(b[(C<<1)-i],R-i+1);//中点公式:i'=2*C-i
while(a[i-b[i]]==a[i+b[i]]) ++b[i];//如果是分支2,就是在b[i]基础上暴力向外扩展;如果是分支1,那么就相当于直接暴力
if(b[i]+i>R) R=b[i]+i-1,C=i;//更新R、C
if(b[i]>ans) ans=b[i];//更新最长回文子串的长度
}
printf("%d",ans-1);//ans直接记录的是新字符串中最长回文的半径,对应到原字符串整个字串的长度只需要-1即可。
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】