dfs序——Tree to Line 的基础

~~看到标题的 Tree to Line 是不是会想到替罪羊树的重构函数 “TtoL” 但其实这俩玩意八竿子打不着~~

基本内容

我们经常会遇到树的问题，但树是非线性的结构，操作起来始终还是麻烦，如果我们能把树改造成线性结构，有什么方法？对，就是今天要讲的DSF序；

dfs序用于树状结构中，如图：

图中红色序号为每个点对应的dfs序序号，黑色序号为每个点默认的序号，我称之为节点序序号（下文同）
可见，dfs序如其名，dfs序序号是按照dfs顺序标记的，所以说给每个节点安排上dfs序序号也很简单，只要dfs的时候顺便标上就行了，dfs第多少次就给dfs到的点标为多少。

void dfs(int x,int fa){
 	dfn[x]=++Time;
	size[x]=1;
 	for(int i=head[x];i;i=nxt[i]){
		int u=to[i];
  		if(u==fa) continue;
		dfs(u,x);
		size[x]+=size[u];
	}
}

dfn存储的就是每个节点的dfs序

Time就是时间戳 和Tarjan中的时间戳大同小异

size是每棵子树的大小

这样做有什么好处？

不难发现对于一颗子树，它内部的dfs序是连续的。所以对于这样的操作：

给x及其子树加上一个值
查询x及其子树点权和

我们就可以转化为在区间上的修改和查询，用线段树来解决。

每棵子树对应的dfs序区间就是 [dfn[x] , dfn[x]+size[x]-1]

一些题

t1

对某个节点x权值加上一个数w

查询某个子树x里所有点权的和

t2

对子树x内的所有节点权值加上一个数w

查询某个节点x的权值

t3

对某个子树x内所有的节点权值加上一个数w

查询某个子树x里所有点权的和

前三题用线段树维护一下就能解决，不再赘述。

t4

节点x的权值加上一个数w

查询节点x到节点y的路径上权值之和

每个点不再只存自己的值，而是存自己到根节点的路径上所有点的权值和。

对于单点修改，考虑其贡献。

当我们给节点 x 的权值加上一个数 w 时，x 的子树内所有节点到根的权值和都会增加 w。

所以单点修改时我们给子树 x 内所有的节点加上 w。

对于路径查询，考虑如何求。

因为每个点存自己到根节点的路径上所有点的权值和。

所以我们可以找到 x,y 的最近公共祖先LCA

如图，a[x]+a[y] 即红色和橙色部分使 lca 多算了一次，lca以上的节点多算了两次，减去蓝色和绿色部分就是我们要的答案，即 -a[lca]-a[fa[lca]]

那么 a[x]+a[y]-a[lca]-a[fa[lca]] 就是路径上的权值和

t5

节点x到节点y的路径上所有节点的权值加上一个数w

查询节点x的值。

利用差分思想，每个路径修改转化为四个点的修改

a[x]+=w,a[y]+=w,a[lca]-=w,a[fa[lca]]-=w

而单点的值就是子树的和。

t6

节点x到节点y的上所有节点的权值加上一个数w

查询子树x内所有节点的权值之和。

如果用 $d e p$ 表示结点深度，那么 ch 到 x 的树链上共有 $d e p_{c h} - d e p_{x} + 1$ 个结点。

每一条树链上的修改对子树的贡献为 $(d e p_{c h} - d e p_{x} + 1) \times v_{c h}$ ，所有树链的贡献之和即为 $\sum [(d e p_{c h} - d e p_{x} + 1) \times v_{c h}]$ 。

拆分式子可得

\sum [(d e p_{c h} + 1) \times v_{c h}] - d e p_{x} \times \sum v_{c h}

所以用两个线段树，分别维护 $\sum [(d e p_{c h} + 1) \times v_{c h}]$ 和 $\sum v_{c h}$ 。

（每次修改时直接在当前节点上加，查询时对子树求和。即单点修改区间求和）

每个路径修改仍然转化为几个点的修改，具体如何转化？首先我们肯定要把 $x, y$ 两个端点的值更新，那 $l c a$ 怎么操作？我们先看看不操作时我们的答案和正确答案差在哪。

原图：模拟求解的正确答案

t1：维护 $\sum [(d e p_{c h} + 1) \times v_{c h}]$

t2：维护 $\sum v_{c h}$

my：我们根据公式求解的答案 $(t 1 - d e p \times t 2)$ 的直观体现

首先，给定一次修改（x，y，v）表示把路径 xy 上所有点点权加上 $v$

对于 dep 小于 $l c a$ 的部分套公式求解的答案与正确答案一致

如图，初始全为空

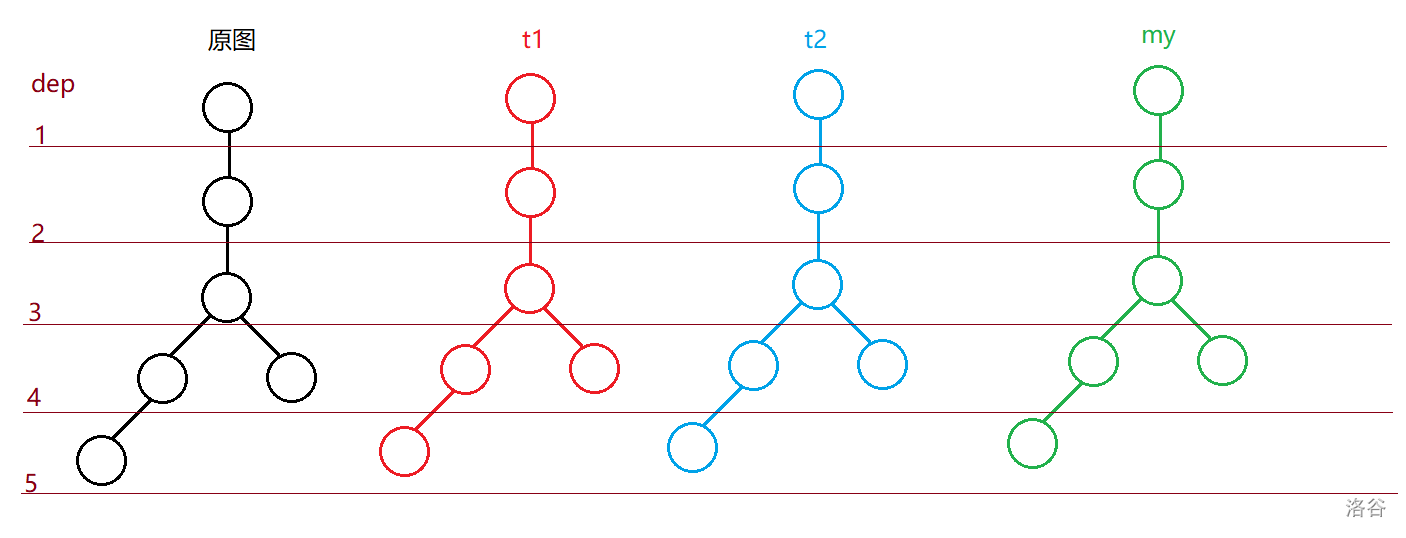
对于 $x, y$ 分别维护 t1，t2

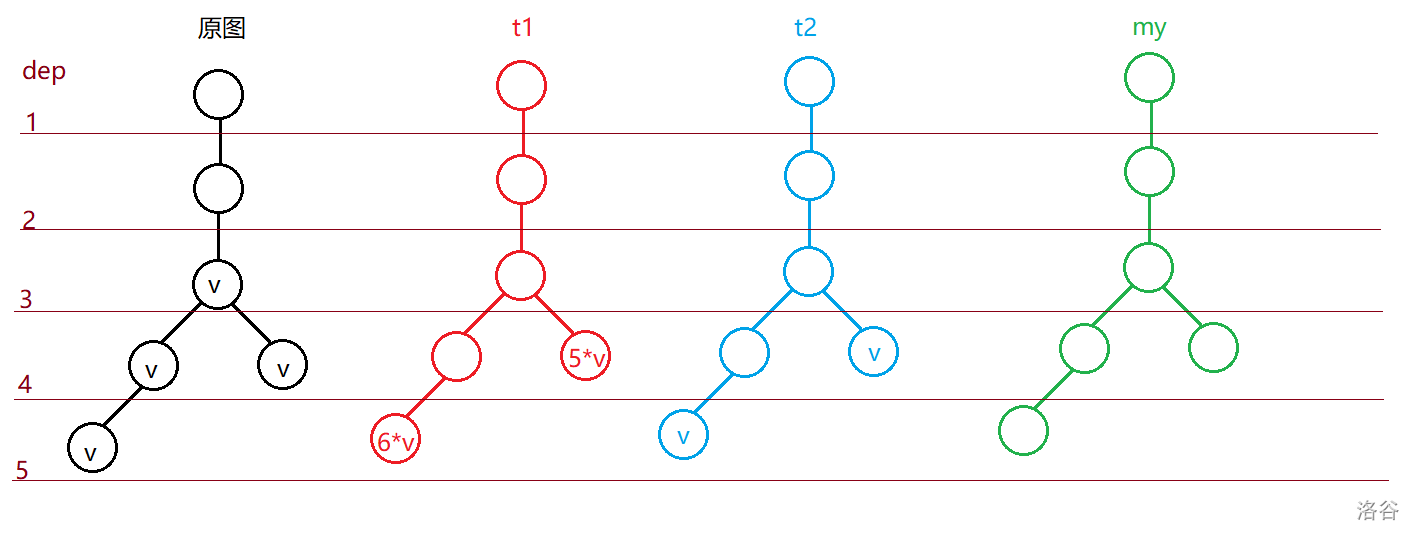
对 $l c a$ 进行查询，可以发现比答案多了 $v$

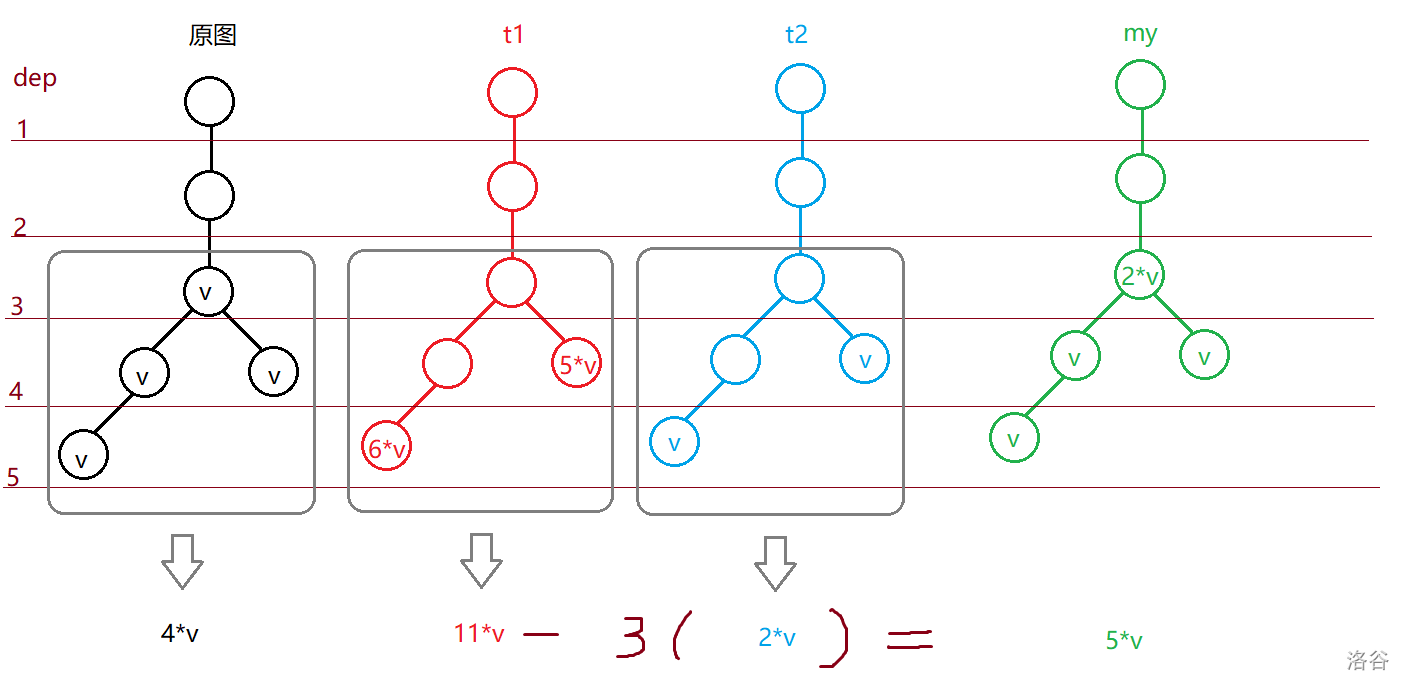
对 $l c a$ 的父亲进行查询，可以发现比答案多了 $v + 2 \times v = 3 \times v$

如果再往上一个进行查询，会比答案多 $v + 2 \times v + 2 \times v = 5 \times v$

之所以会如此，是因为首先lca被多算了一次，而在它之上的每个节点都被多算了两次

但我们不能在每次查询时找之前每次更新的 lca 并减去多余的部分（不好找还费时间），所以只能在更新时在 lca 上做做手脚。

所以我们在维护t1、t2时，在lca这一节点上，t1减去多余的部分，同时t2也要跟着更新。

之前的updata

void Updata(int x,int y,LL val){
	int lca=LCA(x,y);
	t.updata(1,1,n,dfn[x],dfn[x],val*(d[x]+1));
	t.updata(1,1,n,dfn[y],dfn[y],val*(d[y]+1));
	t2.updata(1,1,n,dfn[x],dfn[x],val);
	t2.updata(1,1,n,dfn[y],dfn[y],val);
}

现在的updata

void Updata(int x,int y,LL val){
	int lca=LCA(x,y);
	t.updata(1,1,n,dfn[x],dfn[x],val*(d[x]+1));
	t.updata(1,1,n,dfn[y],dfn[y],val*(d[y]+1));
	t.updata(1,1,n,dfn[lca],dfn[lca],-(d[lca]+1)*2*val+val);
	t2.updata(1,1,n,dfn[x],dfn[x],val);
	t2.updata(1,1,n,dfn[y],dfn[y],val);
	t2.updata(1,1,n,dfn[lca],dfn[lca],-2*val);
}

这部分真的超难理解，建议自己画图推一遍

放下代码吧

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N=200010;
int f[N][26],d[N],dfn[N],cnt,siz[N],n,m;
int head[N],nxt[N<<1],to[N<<1],tot=1;
void add(int x,int y){
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs1(int x,int fa,int deep){
	f[x][0]=fa;
	d[x]=deep;
	dfn[x]=++cnt;
	siz[x]=1;
	for(int i=head[x];i;i=nxt[i]){
		int u=to[i];
		if(u==fa) continue;
		dfs1(u,x,deep+1);
		siz[x]+=siz[u];
	} 
} 
void getfather(){//倍增求LCA
	for(int j=1;j<=log2(n);j++)
		for(int i=1;i<=n;i++)
			f[i][j]=f[f[i][j-1]][j-1];
}
struct TREE{//两颗线段树
	LL sum[N<<2],add[N<<2];
	void pushup(int x){
		sum[x]=sum[x<<1]+sum[x<<1|1];
	}
	void pushdown(int x,int l,int r){
		int mid=(l+r)>>1;
		add[x<<1]+=add[x];
		add[x<<1|1]+=add[x];
		sum[x<<1]+=add[x]*(mid-l+1);
		sum[x<<1|1]+=add[x]*(r-mid);
		add[x]=0;
	}
	void updata(int x,int l,int r,int L,int R,LL val){
		if(l>=L&&r<=R){
			add[x]+=val;
			sum[x]+=val*(r-l+1);
			return;
		}
		int mid=l+r>>1;
		pushdown(x,l,r);
		if(L<=mid) updata(x<<1,l,mid,L,R,val);
		if(R>mid) updata(x<<1|1,mid+1,r,L,R,val);
		pushup(x);
	}
	LL query(int x,int l,int r,int L,int R){
		if(L>R) return 0; 
		if(l>=L&&r<=R) return sum[x];
		int mid=l+r>>1;LL res=0;
		pushdown(x,l,r);
		if(L<=mid) res+=query(x<<1,l,mid,L,R);
		if(R>mid) res+=query(x<<1|1,mid+1,r,L,R);
		return res;
	}
}t,t2;//t就是上文的t1
int LCA(int x,int y){//倍增求LCA
	if(d[x]<d[y]) swap(x,y);
	for(int i=log2(n);i>=0;i--){
		if(d[f[x][i]]>=d[y]) x=f[x][i];
	}
	if(x==y) return x;
	for(int i=log2(n);i>=0;i--){
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	}
	return f[x][0];
}
void Updata(int x,int y,LL val){
	int lca=LCA(x,y);
	t.updata(1,1,n,dfn[x],dfn[x],val*(d[x]+1));
	t.updata(1,1,n,dfn[y],dfn[y],val*(d[y]+1));
	t.updata(1,1,n,dfn[lca],dfn[lca],-(d[lca]+1)*2*val+val);
	t2.updata(1,1,n,dfn[x],dfn[x],val);
	t2.updata(1,1,n,dfn[y],dfn[y],val);
	t2.updata(1,1,n,dfn[lca],dfn[lca],-2*val);
}
LL Query(int x){
	return t.query(1,1,n,dfn[x],dfn[x]+siz[x]-1)-d[x]*t2.query(1,1,n,dfn[x],dfn[x]+siz[x]-1);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,x,y;i<n;i++){
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs1(1,0,1);
	getfather();
	int opt,x,y;
	LL z;
	while(m--){
		scanf("%d",&opt);
		if(opt==1){
			scanf("%d%d%lld",&x,&y,&z);
			Updata(x,y,z);
		}else{
			scanf("%d",&x);
			printf("%lld\n",Query(x));
		}
	}
	return 0;
}

~~累死了~~

t7

节点x子树内所有节点的权值加上一个数w

查询节点x到节点y路径上所有节点的权值之和。

没做，挖坑待填……

posted @ 2022-10-06 14:25 「ycw123」阅读(49) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 线段树初步

· K-D Tree

· 「学习笔记」DFS序和7种模型

· DFS序、倍增、ST表、LCA

· 树的DFS序

阅读排行：
· winform 绘制太阳，地球，月球运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」

公告

昵称：「ycw123」
园龄： 2年5个月
粉丝： 1
关注： 0

+加关注

2025年3月

日

一

二

三

四

五

六

随笔档案 (49)

阅读排行榜

评论排行榜

1. 随机化算法(1)

ycw123

dfs序——Tree to Line 的基础

基本内容

一些题

公告

搜索

常用链接

我的标签

随笔档案 (49)

阅读排行榜

评论排行榜

推荐排行榜

最新评论