【机器学习】梯度下降法
一、简介
梯度下降法(gradient decent)是一个最优化算法,通常也称为最速下降法。常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。
梯度下降法是求解无约束最优化问题的一种最常用的方法,它是一种迭代算法,每一步需要求解目标函数的梯度向量。
问题抽象
是
上具有一阶连续偏导数的函数,要求解的无约束问题是:
, 其中
表示目标函数
的极小值点
关键概念
- 迭代:选取适当初始值
,不断迭代更新
的 值,直至收敛
- 梯度下降:负梯度方向是使函数值下降最快的方向,我们在迭代的每一步都以负梯度方向更新
的值
- 收敛:给定一个精度
,在迭代的每一轮根据梯度函数
计算梯度
,
时认为收敛
- 学习率:也叫做步长,表示在每一步迭代中沿着负梯度方向前进的距离
二、原理
梯度下降法,顾名思义,从高处寻找最佳通往低处的方向,然后下去,直到找到最低点。我们可以看到,J(θ0,θ1)是以θ0,θ1为自变量的函数,它们的关系如图1中所示。图中,起始点的黑色十字从红色的高坡上,一步一步选择最佳的方向通往深蓝色的低谷,这其实就是梯度下降法的作用。
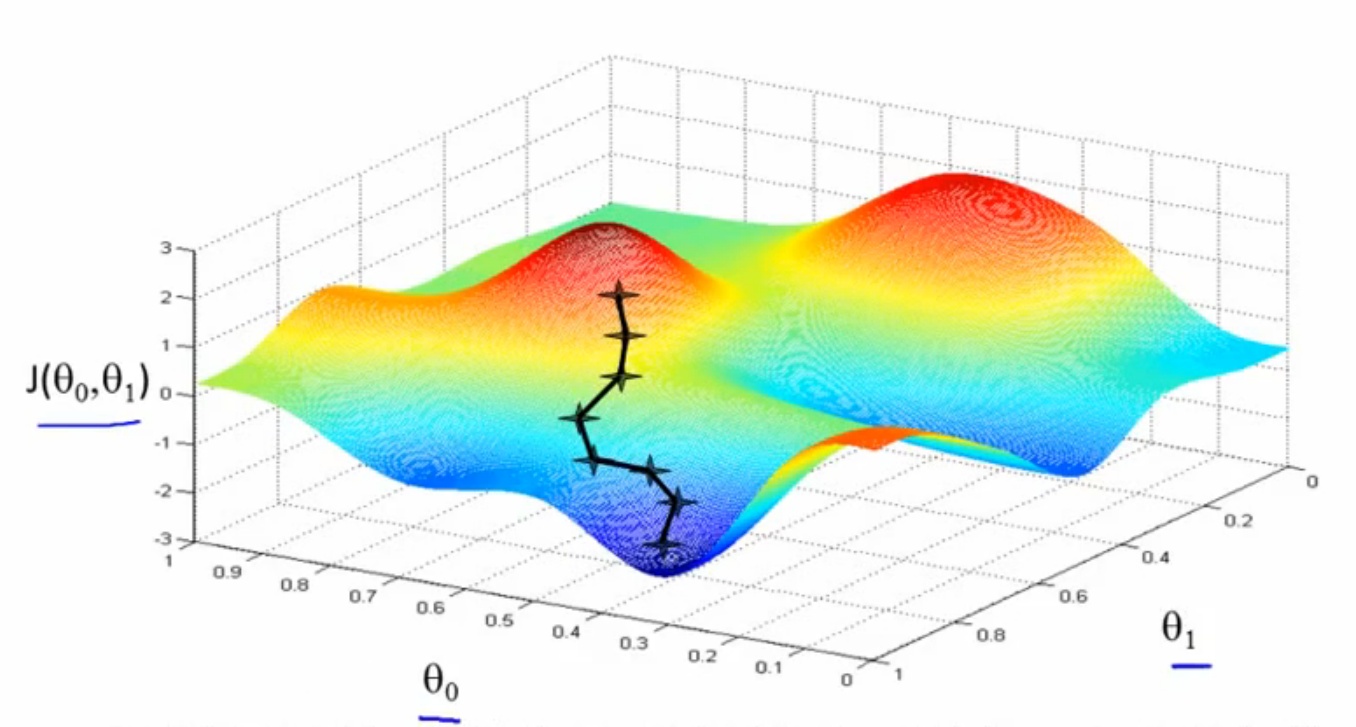
图1
微妙的是图1中的低谷有很多个,选择不同的起始点,最终达到的低谷也会有所不同。如图2所示,黑色十字跑向了另外一个低谷。此时有些人就会问:为什么会产生这种现象?其实,原因很简单,梯度下降法在每次下降的时候都要选择最佳方向,而这个最佳方向是针对局部来考虑的,不同的起始点局部特征都是不同的,选择的最佳方向当然也是不同,导致最后寻找到的极小值并不是全局极小值,而是局部极小值。由此可以看出,梯度下降法只能寻找局部极小值。一般凸函数求极小值时可以使用梯度下降法(当目标函数是凸函数时,梯度下降法是全局的最优解,一般情况下梯度下降法的解不一定是全局最优解)。
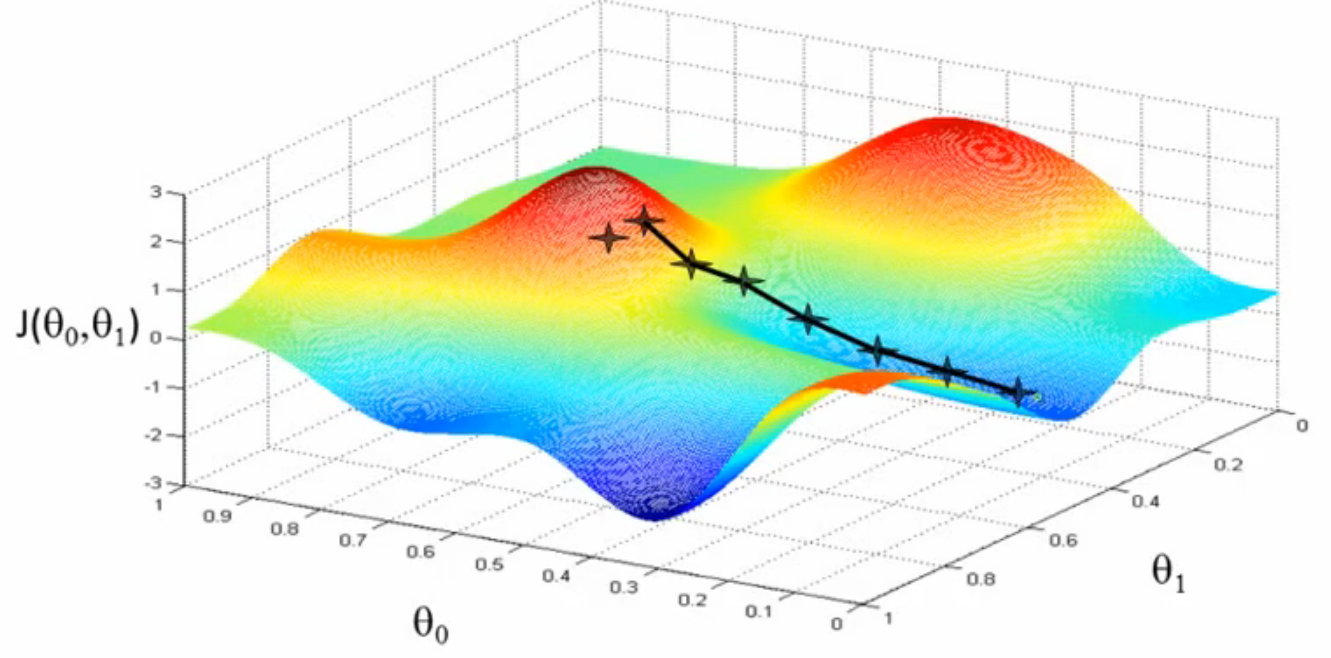
图2
梯度下降法的公式为:
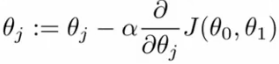 (1)
(1)
公式(1)中“:=”符号代表赋值,并不是代表“等于”,J(θ0,θ1)是需要求极小值的函数。
直观理解
以下图为例,开始时我们处于黑色圆点的初始值(记为 ),我们需要尽快找到函数的最小值点,最快的方法就是沿着坡度最陡的方向往下走
算法细节
由于 具有一阶连续导函数,若第
次迭代值为
,则可将
在
附近进行一阶泰勒展开:
其中 在
的梯度。
接着我们求出第 次的迭代值
:
其中 是搜索方向,取负梯度方向
,
是步长,需满足:
算法实现
- 输入:目标函数
,梯度函数
,计算精度
- 输出:
的极小值点
- 步骤:
- 取初始值
,置
为
- 计算
- 计算梯度
,当
时停止迭代,令
;否则,令
,求
,使
- 令
,计算
,当
或
时停止迭代,令
- 否则,令
,回到步骤3
算法调优
- 学习率:学习率太小时收敛过慢,但太大时又会偏离最优解
- 初始值:当损失函数是凸函数时,梯度下降法得到的解是全局最优解;当损失函数是非凸函数时,得到的解可能是局部最优解,需要随机选取初始值并在多个局部最优解之间比较
- 归一化:如果不归一化,会收敛得比较慢,典型的情况就是出现“之”字型的收敛路径
三、使用方式:以线性回归为例
设线性回归的假设函数为:
![]() (2)
(2)
设代价函数为:
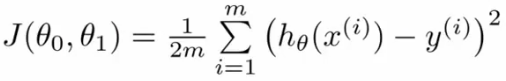 (3)
(3)
目标:寻找J(θ0,θ1)的最小值。
措施:使用梯度下降法
原理:根据公式(1),可以知道求参数θ,下一步的θ是由上一步的θ减去α乘以J(θ0,θ1)在上一点的斜率值产生的,如图3所示,然后不断迭代,当θ值不变时,J(θ0,θ1)达到极小值。
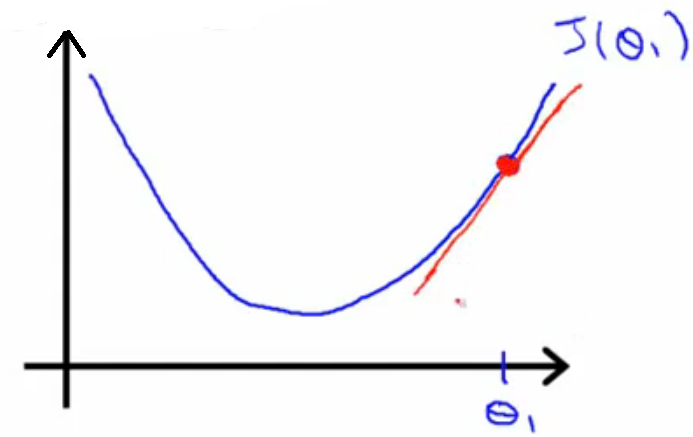
图3
步骤: 不断执行以下公式(4),直到公式(1)收敛,即达到极小值。
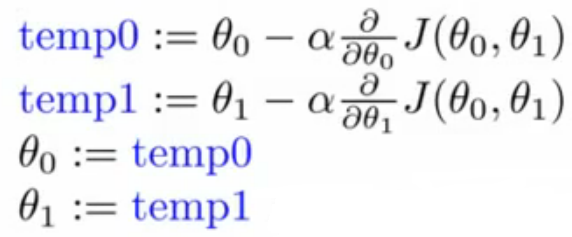
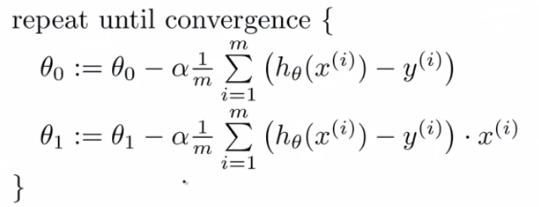 (4)
(4)
注意:公式(4)中各行不能调换顺序,否则并不是梯度下降法
比如公式(5)这种形式,θ0刚更新完,马上就用于下一步的θ1的更新计算,脱离了梯度下降法的意图。
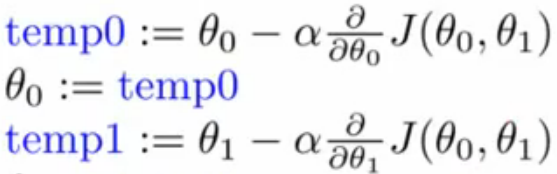 (5)
(5)
四、如何提高梯度下降法的效率
主要有两种方法:
1、特征值x的缩放
why? —— 很多人也许会问:为什么要缩放特征值?缩放特征值x就能提高效率?
用图4来讲解,J(θ)是假设函数hθ(x)=θ0+θ1x1+θ2x2的代价函数,图中J(θ)关于θ1、θ2的等高线图中带箭头的红线是迭代的分步,左边是x1、x2数量级相差较大的时候,红线弯来弯去,迭代效率很低,右边则是x1、x2数量级相差较小的时候,带箭头的红线很快到达了等高线图的最低点,取得极小值,效率很高。所谓的缩放特征值x,就是让所有的x值在数量级上相差不大,达到提高迭代效率的目的。
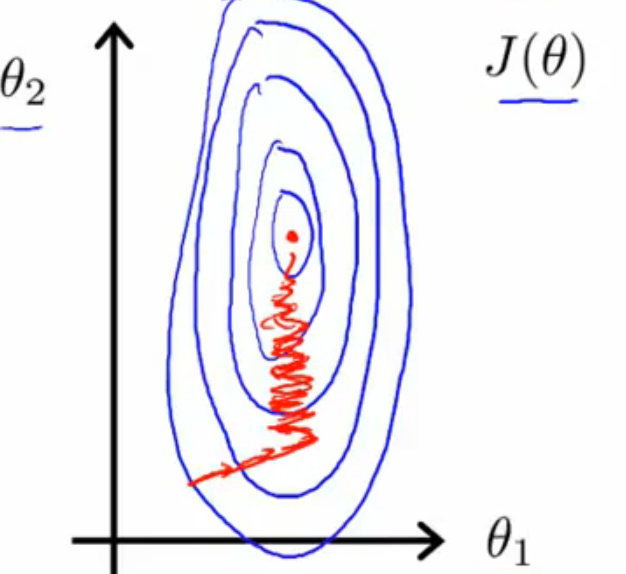
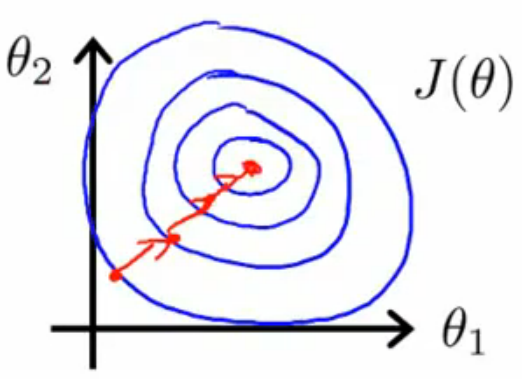
图4
缩放特征值的方法大致有以下三种:
- 除以最大值 (以x1为例,将x1所有样本的值除以max{x1},此时-1≤x1≤1)
- 均值归一化 (x1:=(x1-μ)/(max{x1}-min{x1}),其中μ为x1的平均值,此时-0.5≤x1≤0.5)
- 均值方差归一化
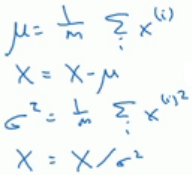
2、选择适当的α
公式(1)中α起着很重要的作用,如果选的太小,则会出现图5左边这种情况,迭代慢;如果选的太大,则会出现图4右边这种情况,过大的α使迭代不收敛。
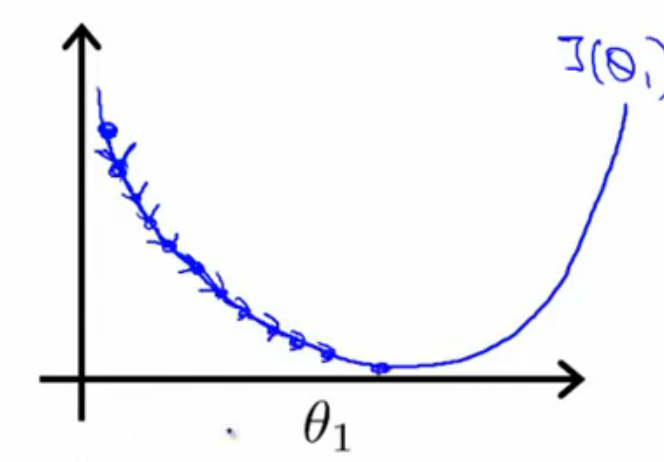
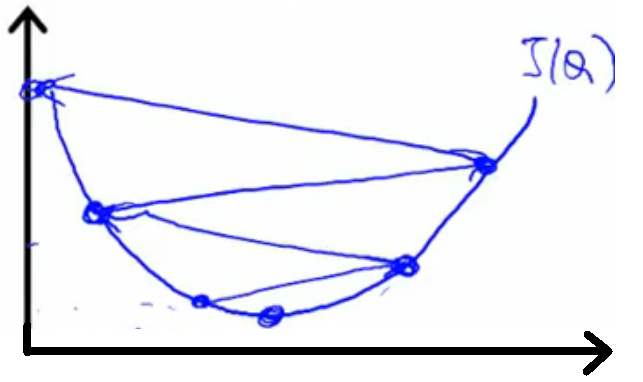
图5
α的选择是需要通过计算一个个试,一般会这样取值(仅限参考):......,0.001,0.003,0.01,0.03,0.1,.........(以此类推)
参考:https://www.cnblogs.com/steed/p/7429804.html
https://zhuanlan.zhihu.com/p/104546744






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通