双三次插值（BiCubic Interpolation）

转载自：(28条消息) 双三次插值（BiCubic插值）_AcceptedLin的博客-CSDN博客_双三次插值

双三次插值（BiCubic Interpolation）

上采样用bicubic填充像素，下采样用相同的方法进行像素剔除。

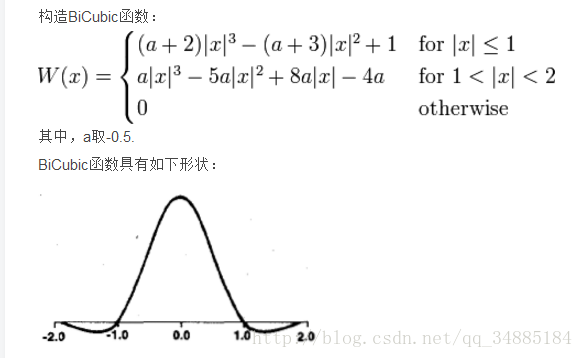
双三次插值又称立方卷积插值。三次卷积插值是一种更加复杂的插值方式。该算法利用待采样点周围16个点的灰度值作三次插值，不仅考虑到4 个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。三次运算可以得到更接近高分辨率图像的放大效果，但也导致了运算量的急剧增加。这种算法需要选取插值基函数来拟合数据，其最常用的插值基函数如图1所示，本次实验采用如图所示函数作为基函数。

 假设源图像A大小为m*n，缩放K倍后的目标图像B的大小为M*N，即K=M/m。A的每一个像素点是已知的，B是未知的，我们想要求出目标图像B中每一像素点(X,Y)的值，必须先找出像素(X,Y)在源图像A中对应的像素(x,y)，再根据源图像A距离像素(x,y)最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数，利用BiCubic基函数求出16个像素点的权重，图B像素(x,y)的值就等于16个像素点的加权叠加。

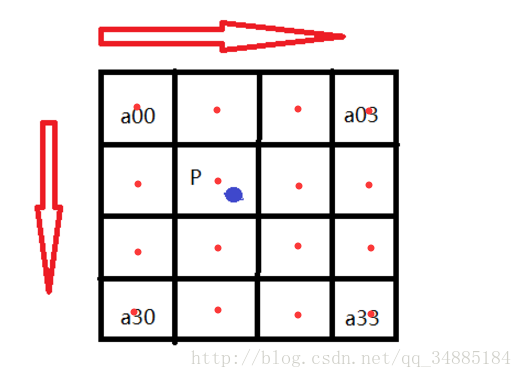
 根据比例关系x/X=m/M=1/K，我们可以得到B(X,Y)在A上的对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))=A(X/K,Y/K)。如图所示P点就是目标图像B在(X,Y)处对应于源图像A中的位置，P的坐标位置会出现小数部分，所以我们假设 P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分（蓝点到a11方格中红点的距离）。那么我们就可以得到如图所示的最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示，如上图。

 

 我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的权重W(x)。BiCubic基函数是一维的，而像素是二维的，所以我们将像素点的行与列分开计算。BiCubic函数中的参数x表示该像素点到P点的距离，例如a00距离P(x+u,y+v)的距离为(1+u,1+v)，因此a00的横坐标权重i_0=W(1+u)，纵坐标权重j_0=W(1+v)，a00对B(X,Y)的贡献值为：（a00像素值）* i_0* j_0。因此，a0X的横坐标权重分别为W(1+u)，W(u)，W(1-u)，W(2-u)；ay0的纵坐标权重分别为W(1+v)，W(v)，W(1-v)，W(2-v)；B(X,Y)像素值为：

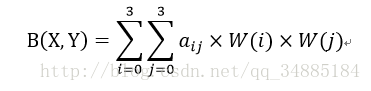
上述可以用矩阵形式表示，下面图片来源：图像处理中的双三次插值-CSDN社区

加权算法（原作者推理，a取-0.5效果最好，但a也可以不取-0.5）：