Attention is all you need (二)pytorch实现encoder中的word embedding,position embedding,self-attention mask
Attention is all you need原文提供的代码是基于Tensor2Tensor的。因为现在学术界比较常用pytorch,所以我就去找了一下pytorch实现的相关资料。
参考:19、Transformer模型Encoder原理精讲及其PyTorch逐行实现_哔哩哔哩_bilibili
这个up主讲得很细致。下面我也只是跟着他一步一步把视频中的代码码出来,并写一些自己的见解。
前言:最近试了一下jupyter-lab。感觉还不错,是jupyter notebook的升级版,在此记录一下jupyter-lab的使用与安装。
参考:JupyterLab的安装及使用Python虚拟环境 - 知乎 (zhihu.com)
1、安装JupyterLab
pip install jupyterlab
2、激活虚拟环境
在terminal中输入命令:
conda activate torch_gpu
其中torch_gpu是我创建的虚拟环境的名字。
3、使用Python虚拟环境
如果你创建了一个Python虚拟环境,那么首先进入到这个虚拟环境中,然后运行命令:
python -m ipykernel install --user --name=torch_gpu
接着在terminal中输入命令,打开jupyterLab:
jupyter-lab
这样就可以在JupyterLab中使用这个虚拟环境了。
在jupyter中可以看到有torch_gpu这个虚拟环境的notebook创建选项。

下面回来transformer encoder中word embedding,position embedding,self-attention mask的pytorch实现。
(一)word embedding
import torch import numpy as np import torch.nn as nn import torch.nn.functional as F #关于word embedding,以序列建模为例 #考虑source sentence 和 target sentence #构建序列,序列的字符以其在词表中的索引的形式表示 batch_size=2 #单词表大小 max_num_src_words=8 max_num_tgt_words=8 model_dim=8 #序列的最大长度 max_src_seq_len=5 max_tgt_seq_len=5 max_position_len=5
先导入库,和设置一些全局变量。为了能让后面的print看起来更加直观,理解起来更加方便,这些全局变量设置得比较简单。
#src_len=torch.randint(2,5,(batch_size,)) #tgt_len=torch.randint(2,5,(batch_size,)) src_len=torch.Tensor([2,4]).to(torch.int32) tgt_len=torch.Tensor([4,3]).to(torch.int32) #单词索引构成源句子和目标句子,构建batch,并且做了padding,默认值为0 src_seq=torch.stack([F.pad(torch.randint(1,max_num_src_words,(L,)),(0,max(src_len)-L)) for L in src_len]) tgt_seq=torch.stack([F.pad(torch.randint(1,max_num_tgt_words,(L,)),(0,max(tgt_len)-L)) for L in tgt_len]) #构造embedding src_embedding_table=nn.Embedding(max_num_src_words+1,model_dim) tgt_embedding_table=nn.Embedding(max_num_tgt_words+1,model_dim) src_embedding=src_embedding_table(src_seq) tgt_embedding=tgt_embedding_table(tgt_seq)
print("#output") print("src_len:",src_len) print("tgt_len:",tgt_len) print("src_seq:",src_seq) print("tgt_seq:",tgt_seq) print("src_embedding_table:",src_embedding_table.weight) print("tgt_embedding_table:",tgt_embedding_table.weight) print("src_embedding:",src_embedding) print("tgt_embedding:",tgt_embedding)
#output src_len: tensor([2, 4], dtype=torch.int32) #每个batch两个句子,source句子的长度分别设置为2和4 tgt_len: tensor([4, 3], dtype=torch.int32) #每个batch两个句子,target句子的长度分别设置为4和3
src_seq: tensor([[5, 4, 0, 0], #从单词表中引入单词的索引并且做padding
[2, 4, 5, 5]]) #例如第一个句子长度是2,由索引分别为5和4的单词构成。为了保证输入句子长度一致,后面还需要填充两个0
tgt_seq: tensor([[2, 5, 6, 5],
[7, 2, 5, 0]])
#对每个单词进行embedding,8个单词+1个padding=9,d_model=8表示对一个单词做8维的embedding
tensor([[ 0.3850, -0.0602, -1.8317, 0.6519, 1.2455, 1.0001, 0.4022, 1.1223],
[ 0.2892, -0.0932, 0.7463, -0.0331, 0.3940, 0.9937, -0.3547, -0.7878],
[-0.0556, -0.6444, -0.4716, 0.4150, 0.9155, 0.5646, 0.0329, 0.1278],
[-1.2203, -1.8609, 0.3123, -0.8658, 0.2041, -0.0335, -0.0137, 0.9465],
[-1.0230, 1.2947, -1.3639, -0.0634, 1.0648, 0.5289, -0.5729, -1.1670],
[ 0.2552, 0.5546, -0.3588, -0.2794, -0.7291, -0.3943, -1.5113, 2.1280],
[ 0.2892, -1.0773, -0.5164, -0.2380, -1.0530, -0.1422, -0.0585, -0.5485],
[ 0.2658, 1.1549, 0.5389, -0.3361, 0.3259, -0.4918, 0.4084, -1.3230],
[ 0.7355, -0.2094, -1.6005, -0.5678, -0.1358, -1.0172, 0.3401, -0.0267]],
requires_grad=True)
tgt_embedding_table: Parameter containing:
tensor([[-1.2169, 0.3871, 0.0095, -0.9160, -0.4130, 0.2967, -0.1636, 0.4938],
[-1.1897, 0.5324, 1.6332, -0.0652, -0.5156, -0.3866, 0.3502, -0.0642],
[-2.5679, -0.9219, -0.1279, 0.0405, 0.3109, -0.3668, -0.0948, -0.3985],
[-0.3280, 2.4640, 0.2466, 0.2708, 0.9492, -0.3630, -0.8543, -0.9339],
[ 0.2985, -0.5360, 0.5909, -1.7827, 0.7939, 0.9598, -0.3641, 0.9780],
[ 1.4359, -1.8412, 1.1170, 0.5556, 0.0084, 0.1511, -1.9965, 0.7734],
[ 0.6577, 0.5102, -0.6020, 0.6097, -0.3272, 1.2983, 0.3544, -0.4470],
[ 0.4795, -0.5372, 1.1872, 0.1083, -0.5515, 1.0481, 0.7195, 0.5965],
[ 0.3768, 1.1607, 1.0981, -1.4396, 0.8362, 1.1354, 0.7623, -0.8735]],
requires_grad=True)
#根据seq在table中查询
src_embedding: tensor([[[ 0.2552, 0.5546, -0.3588, -0.2794, -0.7291, -0.3943, -1.5113, 2.1280], [-1.0230, 1.2947, -1.3639, -0.0634, 1.0648, 0.5289, -0.5729, -1.1670], [ 0.3850, -0.0602, -1.8317, 0.6519, 1.2455, 1.0001, 0.4022, 1.1223], [ 0.3850, -0.0602, -1.8317, 0.6519, 1.2455, 1.0001, 0.4022, 1.1223]], [[-0.0556, -0.6444, -0.4716, 0.4150, 0.9155, 0.5646, 0.0329, 0.1278], [-1.0230, 1.2947, -1.3639, -0.0634, 1.0648, 0.5289, -0.5729, -1.1670], [ 0.2552, 0.5546, -0.3588, -0.2794, -0.7291, -0.3943, -1.5113, 2.1280], [ 0.2552, 0.5546, -0.3588, -0.2794, -0.7291, -0.3943, -1.5113, 2.1280]]], grad_fn=<EmbeddingBackward0>) tgt_embedding: tensor([[[-2.5679, -0.9219, -0.1279, 0.0405, 0.3109, -0.3668, -0.0948, -0.3985], [ 1.4359, -1.8412, 1.1170, 0.5556, 0.0084, 0.1511, -1.9965, 0.7734], [ 0.6577, 0.5102, -0.6020, 0.6097, -0.3272, 1.2983, 0.3544, -0.4470], [ 1.4359, -1.8412, 1.1170, 0.5556, 0.0084, 0.1511, -1.9965, 0.7734]], [[ 0.4795, -0.5372, 1.1872, 0.1083, -0.5515, 1.0481, 0.7195, 0.5965], [-2.5679, -0.9219, -0.1279, 0.0405, 0.3109, -0.3668, -0.0948, -0.3985], [ 1.4359, -1.8412, 1.1170, 0.5556, 0.0084, 0.1511, -1.9965, 0.7734], [-1.2169, 0.3871, 0.0095, -0.9160, -0.4130, 0.2967, -0.1636, 0.4938]]], grad_fn=<EmbeddingBackward0>)
(二)position embedding
类似于word embedding。还是调用pytorch的embedding API来实现(但是我觉得没必要)
#构造position embedding pos_mat=torch.arange(max_position_len).reshape(-1,1) i_mat=torch.pow(10000,torch.arange(0,8,2).reshape(1,-1)/model_dim) pe_embedding_table=torch.zeros(max_position_len,model_dim) pe_embedding_table[:,0::2]=torch.sin(pos_mat/i_mat) pe_embedding_table[:,1::2]=torch.cos(pos_mat/i_mat) pe_embedding=nn.Embedding(max_position_len,model_dim) pe_embedding.weight=nn.Parameter(pe_embedding_table,requires_grad=False) src_seq=torch.stack([torch.arange(max(src_len)) for _ in src_len]).to(torch.int32) tgt_seq=torch.stack([torch.arange(max(tgt_len)) for _ in tgt_len]).to(torch.int32) src_pe_embedding=pe_embedding(src_seq) tgt_pe_embedding=pe_embedding(tgt_seq)
使用公式如下:
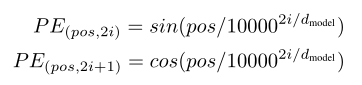
具体可看原论文。或者Attention is all you need (一)公式和图表解读笔记 - 实数集 - 博客园 (cnblogs.com)
(三)self-attention mask
在multi-head attention中的scaled dot-product attention模块会经过softmax算Q和K关联的概率。所以我们要把之前padding的那部分mask掉,即替换成一个非常小的数,这样在softmax算概率padding部分的值会变成0。
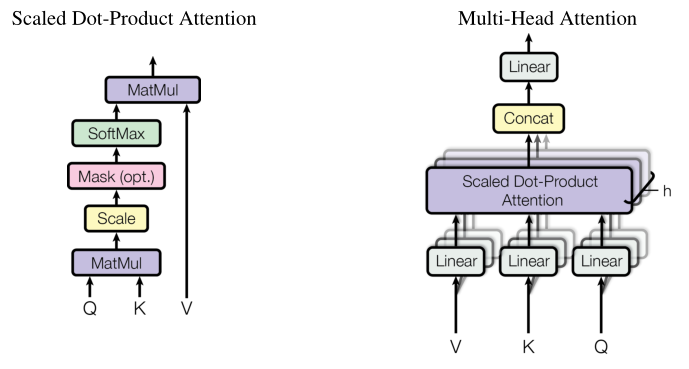
下面代码是构造邻接矩阵,能直观看到每个词之间的关联性。
#构造encoder的self-attention mask #mask的shape:[batch_size,max_src_len,max_src_len],值为1或-inf valid_encoder_pos=torch.unsqueeze(torch.stack([F.pad(torch.ones(L),(0,max(src_len)-L)) for L in src_len]),2) valid_encoder_pos_matrix=torch.bmm(valid_encoder_pos,valid_encoder_pos.transpose(1,2)) invalid_encoder_pos_matrix=1-valid_encoder_pos_matrix mask_encoder_self_attention=invalid_encoder_pos_matrix.to(torch.bool) score=torch.randn(batch_size,max(src_len),max(src_len)) masked_score=score.masked_fill(mask_encoder_self_attention,-1e9) prob=F.softmax(masked_score,-1) print(prob)
例如第一个长度为2的句子中第一个词与第一个词的关联概率是0.1904。
#output tensor([[[0.1904, 0.8096, 0.0000, 0.0000], [0.1424, 0.8576, 0.0000, 0.0000], [0.2500, 0.2500, 0.2500, 0.2500], [0.2500, 0.2500, 0.2500, 0.2500]], [[0.4810, 0.1547, 0.0939, 0.2704], [0.2752, 0.1542, 0.4731, 0.0975], [0.2868, 0.1464, 0.4278, 0.1390], [0.1463, 0.6821, 0.1574, 0.0142]]])
补充:scaled的必要性
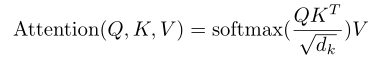
除以根号dk,就是scaled。
#softmax演示,scaled的重要性 alpha1=0.1 alpha2=10 score=torch.randn(5) prob1=F.softmax(score*alpha1,-1) prob2=F.softmax(score*alpha2,-1) def softmax_func(score): return F.softmax(score) jaco_mat1=torch.autograd.functional.jacobian(softmax_func,score*alpha1) jaco_mat2=torch.autograd.functional.jacobian(softmax_func,score*alpha2) print(jaco_mat1) print(jaco_mat2)
#output tensor([[ 0.1607, -0.0389, -0.0441, -0.0404, -0.0372], [-0.0389, 0.1560, -0.0424, -0.0389, -0.0358], [-0.0441, -0.0424, 0.1713, -0.0441, -0.0406], [-0.0404, -0.0389, -0.0441, 0.1606, -0.0372], [-0.0372, -0.0358, -0.0406, -0.0372, 0.1508]]) tensor([[ 1.6231e-04, -5.0437e-10, -1.6229e-04, -2.4321e-08, -6.5893e-12], [-5.0437e-10, 3.1069e-06, -3.1059e-06, -4.6546e-10, -1.2611e-13], [-1.6229e-04, -3.1059e-06, 3.1509e-04, -1.4977e-04, -4.0577e-08], [-2.4321e-08, -4.6546e-10, -1.4977e-04, 1.4979e-04, -6.0810e-12], [-6.5893e-12, -1.2611e-13, -4.0577e-08, -6.0810e-12, 4.0590e-08]])
可以看到,scaled的雅可比矩阵有数值正常。没有scaled的雅可比矩阵方差太大了,这会导致梯度消失等一系列问题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号