线性代数：向量空间学习笔记
线性代数及其应用.David C. Lay
1.向量空间与子空间
定义：向量空间
一个向量空间是由一些被称为向量的对象构成的非空集合\(V\)，在这个集合上定义两个运算，称为加法和标量乘法（标量取实数），服从以下公理（或法则），这些公理必须对\(V\)中所有向量\(\boldsymbol{u}\)，\(\boldsymbol{v}\)，\(\boldsymbol{w}\)及所有标量\(c\)和\(d\)均成立。
- \(\boldsymbol{u}\)，\(\boldsymbol{v}\)之和表示为\(\boldsymbol{u}+\boldsymbol{v}\)，仍在\(V\)中。
- \(\boldsymbol{u}+\boldsymbol{v}=\boldsymbol{v}+\boldsymbol{u}\).
- \((\boldsymbol{u}+\boldsymbol{v})+\boldsymbol{w}=\boldsymbol{u}+(\boldsymbol{v}+\boldsymbol{w})\).
- \(V\)中存在一个零向量\(\bf{0}\)，使得\(\boldsymbol{u}+\boldsymbol{0}=\boldsymbol{u}\).
- 对\(V\)中每个向量\(\boldsymbol{u}\)，存在\(V\)中向量\(-\boldsymbol{u}\)，使得\(\boldsymbol{u}+(-\boldsymbol{u})=\bf{0}\).
- \(\boldsymbol{u}\)与标量\(c\)的标量乘法记为\(c\boldsymbol{u}\)，仍在\(V\)中。
- \(c(\boldsymbol{u}+\boldsymbol{v})=c\boldsymbol{u}+c\boldsymbol{v}\).
- \((c+d)\boldsymbol{u}=c\boldsymbol{u}+d\boldsymbol{u}\).
- \(c(d\boldsymbol{u})=(cd)\boldsymbol{u}\).
- \(1\boldsymbol{u}=\boldsymbol{u}\).
定义：子空间
向量空间\(V\)的一个子空间是\(V\)的子集\(H\)，且满足以下三个性质：
定理1：
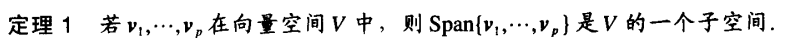
2.零空间、列空间和线性变换
定义：零空间
定理2：
定义：列空间
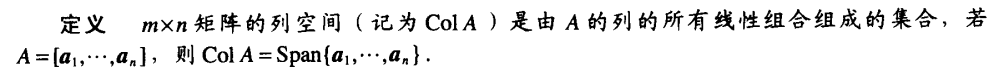
定理3：
定义：线性变换
3.线性无关集和基
定义：线性无关和线性相关
定理4
定义：基
定理5：生成集定理
矩形框
矩阵的行初等变换不影响矩阵的列的线性相关关系。
定理6：
矩阵\(A\)的主元列构成\({\rm Col}\ A\)的一个基。
4.坐标系
定理7（惟一表示定理）：
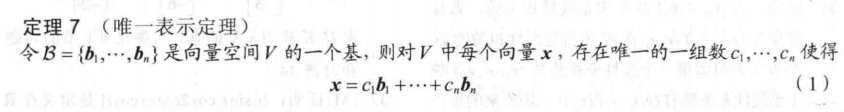
定义：坐标
坐标变换矩阵
定理8：
5.向量空间的维数
定理9：
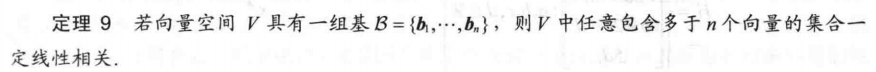
定理10：
若向量空间\(V\)有一组基含有\(n\)个向量，则\(V\)的每一组基一定恰好含有\(n\)个向量.
定义：维数
定理11：
定理12（基定理）：
令\(V\)是一个\(p\)维向量空间，\(p\ge 1\)，\(V\)中任意含有\(p\)个元素的线性无关集必然是\(V\)的一个基.任意含有\(p\)个元素且生成\(V\)的集合自然是\(V\)的一个基.
矩形框
6.秩
行空间定义：若\(A\)是一个\(m\times n\)矩阵，\(A\)的每一行具有\(n\)个元素，即可以视为\(\mathbb{R}^n\)中一个向量。其行向量的所有线性组合的集合称为\(A\)的行空间，记为\(\text{Row} A\).
注：可以用\(\text{Col} A^{\text{T}}\)代替\(\text{Row} A\).
定理13：若两个矩阵\(A\)和\(B\)行等价，则它们的行空间相同。若\(B\)是阶梯形矩阵，则\(B\)的非零行构成\(A\)的行空间的一个基，同时也是\(B\)的行空间的一个基。
秩定义：\(A\)的秩即\(A\)的列空间的维数。
定理14（秩定理）：
todo
