写给草履虫的数字信号处理：第2章 系统

第2章 系统

2.1 系统
2.2 系统互联
2.3 系统的性质
2.4 线性时不变系统
（初稿 2022.9.14）

2.1 系统

系统是将信号作为输入，并产生输出信号的过程或多个过程的组合。例如，一个有信号输入并产生了放大输出信号的放大器，就是一个系统。

处理连续时间信号并且产生连续时间输出信号的系统，称为连续时间系统：
\(x(t) \to y(t)\)

相似地，处理离散时间信号并且产生离散时间输出信号的系统，称为离散时间系统：
\(x[n] \to y[n]\)

2.2 系统互联

工程师经常将称为子系统的许多小系统连接到一起，从而形成一个新系统。这样做的一个明显的优点在于，对许多小系统建模比建模一个大系统来得简单。不过这显然存在一个问题，我们该如何用子系统的行为来描述整个大系统的行为。
接下来让我们看下几种连接类型。

2.2.1 串联或级联

图 2.2-1 系统串联

串联（或级联）是最简单的系统连接方式。其仅仅是将多个系统一个接一个地连接起来。其定义如下：
\(y(t)=H_2(H_1(t))\)

举例：一个无线电接收机之后连接着一个放大器。

2.2.2 并联

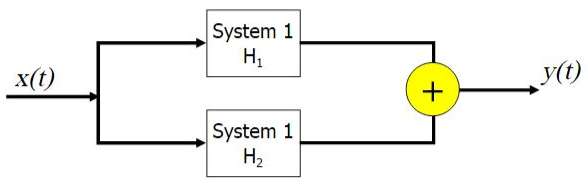
图 2.2-2 系统并联

并联是另一个系统互联形式。在一个并联系统中，相同的输入送给两个或以上的子系统，并在末端将相应的输出累加起来。其定义如下：
\(y(t) = H_2(x(t)) + H_1(x(t))\)

举例：电话线并联连接着多个电话麦克风。

2.2.3 反馈连接

前述两种连接中，系统的输入与输出完全无关。但是在反馈连接中，系统会利用输出信号。
对于正反馈系统：\(y(t)=H_1(x(t))+H_2(y(t))\)，
对于负反馈系统：\(y(t)=H_1(x(t))-H_2(y(t))\)。

2.3 系统的性质

本节中我们介绍一些连续和离散时间系统的基本性质。

2.3.1 记忆性

如果系统的输出只取决于当前时刻的输入，则称为无记忆系统。即该系统无法记忆过去发生的事情，也无法预测未来（排队占星师）。例如，在电阻器上的电压-电流关系：\(i(t)=v(t)/R\).

\(t=2\)时刻的电流，仅取决于\(t=2\)时刻的电压。\(t=0或1\)或其它时刻的电压对\(t=2\)时刻的电流没有影响。
在有记忆系统中，过去或将来的输入会决定现在的输出。例如，\(y(t)=x(t-1)\).

在该系统中，\(t=2\)时刻的系统输出\(y(2)\)取决于\(t=1\)时刻的输入，即\(x(2-1)=x(1)\)。因此，该系统有记忆性。

2.3.2 因果性

当系统的输出仅取决于当前或过去时刻的输入值，该系统称为因果系统。换句话说，因果系统不考虑未来的输入值。
例如，\(y(t)=x(t+1)\)。
在该系统中，\(t=2\)时刻的系统输出\(y(2)\)取决于\(t=3\)时刻，即\(x(2+1)=x(3)\)。因此，该系统不是因果系统。
所有实时物理系统都是因果的，因为时间只会向前流逝。结果发生于原因之后。（相像下一个非因果系统，你今天的收入取决于你一年之后的工作。）

2.3.3 时不变性

一个系统被称为时不变，是指其行为不随着时间的变化而变化。因此，不管是下午6时、下午12时或是其它任何时间，系统的行为都是确定不变的。换句话说，在时不变系统中，输入信号的时移会引起输出信号的时移。
例如，如果系统为\(y(t)=x(t)\)，则\(y(t-1)=x(t-1)\)。
该系统具有时不变性，因为延迟了一个时间单位的输入信号（注：原文为1秒），产生的输出信号也延迟了一秒。

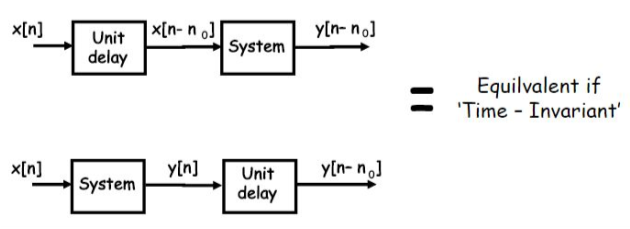
图 2.3-1 时不变性

2.3.4 稳定性

稳定性是一种重要的系统性质。一个稳定系统是指当输入小信号时，不会产生剧烈的输出响应。换句话说，一个有限的输入应该产生一个有限的、而不是失去控制的输出。在数字信号处理中，我们用术语BIBO（Bounded Input Bounded Output）来定义系统的稳定性，即有界输入有界输出。
例如，考虑系统\(y(t)=t x(t)\)。
当\(x(t)=2\)时，\(y(t)=2t\)，该输出值就是无界的。因此，该系统是无界系统（注：也是不稳定系统）。不稳定系统会导致难以预测的响应，并且难以控制。

2.3.5 线性

线性应该是最重要的系统性质。遵循叠加性质的系统称为线性系统。叠加性质基本上是两个系统特性的组合：
1.可加性
两个或以上输入信号之和的响应，等于每个信号单独的响应之和。有\(x_1(t)\to y_1(t)\)和\(x_2(t)\to y_2(t)\)，假设满足\(x_1(t)+x_2(t)\to y_1(t)+y_2(t)\)，则称该系统具有可加性。

2.齐次性或尺度变换性

一个缩放输入信号的系统响应，与原信号的系统响应的缩放结果一致。假设原信号的响应为\(x(t)\to y(t)\)，则当\({\text a} x(t) \to {\text a} y(t)\)，则称该系统为齐次性，其中\({\text a}\)为常数。

将上述两种性质合起来，我们得到叠加的性质：
\({\text a} x_1(t) + {\text b} x_2(t) \to {\text a} y_1(t)+{\text b} y_2(t)\)

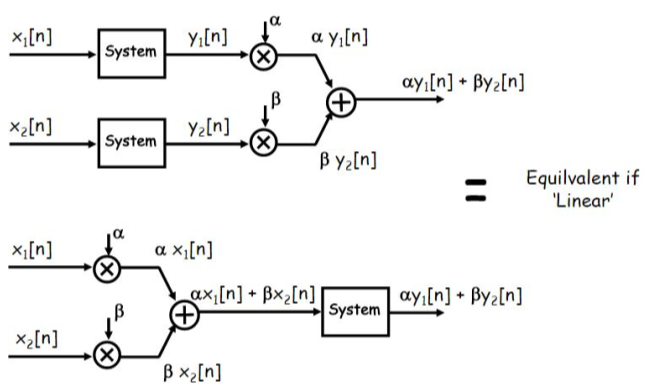
图 2.3-2 系统的线性

从这个性质中我们可以得到一个有趣的发现，对于线性系统，零输入会产生零输出（假设\({\text a}=0\)，则输出为零）。
虽然本小节的性质定义都采用连续时间信号，但是对于离散时间信号，这些性质也是成立的。

2.4 线性时不变系统

事实上，真实世界中的系统很少是线性时不变的。但是更多的时候，我们将真实世界建模为线性时不变系统（LTI）。这样做是有充分理由的。LTI系统更容易进行分析和研究。其数学处理简单很多，并且可以使用更多数学工具进行分析。正如理查德·费曼所说：“线性系统如此重要，正因为我们可以解决它。”采用线性系统进行近似所带来的好处，远比其带来的坏处多得多。即使是高度非线性系统在分析时也被当作LTI系统，随后会再对非线性进行调整。
从现在开始，本书中提及的任何系统都是LTI系统。几种LTI系统的性质，包括非常重要的卷积性质，接下来将会被讨论到。