普林斯顿微积分读本:学习笔记
目录
第1章 函数、图像和直线
1.5 线性函数的图像
如果已知直线通过点 \((x_0, y_0)\), 斜率为 \(m\), 则它的方程为 \(y−y_0 = m(x−x_0)\).
如果一条直线通过点 \((x_1, y_1)\) 和 \((x_2, y_2)\), 则它的斜率等于 \(\frac{y_2 − y_1}{x_2 − x_1}\).
1.6 常见函数及其图像
1.多项式
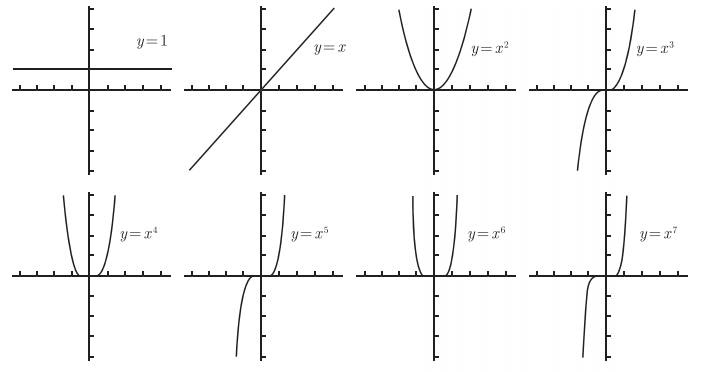
图 1-15 多项式
2.有理函数
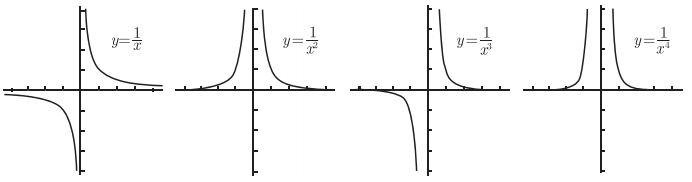
图 1-17 有理函数
3.指数函数和对数函数
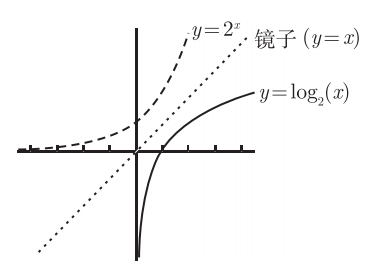
图 1-20 指数函数和对数函数
4.三角函数(见第二章)
5.带有绝对值的函数
\(
\left|x \right| =
\begin{cases}
x, & \text{如果}x\ge 0 \\
-x, & \text{如果}x < 0
\end{cases}
\)
\(\left|x-y \right|\)是数轴上 \(x\) 和 \(y\) 两点间的距离.
第2章 三角学回顾
2.1 基本知识
\(\sin(\theta)=\frac{对边}{斜边}\),\(\cos(\theta)=\frac{邻边}{斜边}\), \(\tan(\theta)=\frac{对边}{邻边}\)
\(\csc(x)=\frac{1}{\sin(x)}\),\(\sec(x)=\frac{1}{\cos(x)}\),\(\cot(x)=\frac{1}{\tan(x)}\)

2.2 扩展三角函数定义域
ASTC 方法
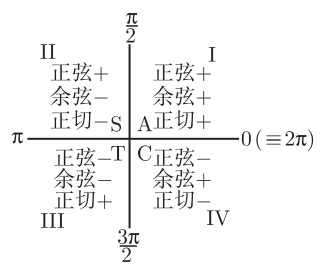
图 2-10 ASTC方法
2.3 三角函数的图像
\(\sin (x)\)、\(\tan (x)\)、\(\cot (x)\), 及 \(\csc (x)\) 都是 x 的奇函数. \(\cos (x)\) 和 \(\sec (x)\) 都是 \(x\) 的偶函数.
2.4 三角恒等式
\(\cos^2(x)+\sin^2(x)=1\)
\(1+\tan^2(x)=\sec^2(x)\)
\(\cot^2(x)+1=\csc^2(x)\)
\(三角函数(x)={\text co-}三角函数 \left(\frac{\pi}{2}-x \right)\)
和角公式
\(\sin(A+B)=\sin(A)\cos(B)+\cos(A)\sin(B)\)
\(\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)\)
倍角公式
\(\sin(2x)=2\sin(x)\cos(x)\)
\(\cos(2x)=2\cos^2(x)-1=1-2\sin^2(x)\)
第3章 极限导论
3.6 三明治定理(夹逼定理)
如果对于所有在\(a\)附近的\(x\)都有\(g(x)\le f(x) \le h(x)\),且\(\lim_{n \to a}g(x)=\lim_{n \to a}h(x)=L\),则\(\lim_{n \to a}f(x)=L\)。
第4章 求解多项式的极限问题
4.1 $x \to a $时的有理函数的极限
形如\(\lim_{x \to a}\frac{p(x)}{q(x)}\).
例题:
\(\lim_{x \to -1}\frac{x^2-3x+2}{x-2}\),
\(\lim_{x \to 2}\frac{x^2-3x+2}{x-2}\),
\(\lim_{x \to 3}\frac{x^3-27}{x^4-5x^3+6x^2}\),
分母为零分子不为零:
\(\lim_{x \to 1}\frac{2x^2-x-6}{x(x-1)^3}\),
\(\lim_{x \to 1}\frac{2x^2-x-6}{x(x-1)^2}\).
立方差公式:\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
4.2 $x \to a $时的平方根的极限
todo
第5章 连续性和可导性
5.1 连续性
如果\(\lim_{x \to a}f(x)=f(a)\),函数\(f\)在点\(x=a\)处连续。
介值定理:如果\(f\)在\([a,b]\)上连续,并且\(f(a)<0\)且\(f(b)>0\),那么在区间\((a,b)\)上至少有一点\(c\),使得\(f(c)=0\)。代之以\(f(a)>0\)且\(f(b)<0\),同样成立。
最大值与最小值定理:如果\(f\)在\([a,b]\)上连续,那么\(f\)在\([a,b]\)上至少有一个最大值和一个最小值。
第7章 三角函数的极限和导数
7.1 三角函数的极限
小数的情况:
\(\lim_{x \to 0}\frac{\sin(x)}{x}=1\)
\(\lim_{x \to 0} \cos(x)=1\)
\(\lim_{x \to 0}\frac{\tan(x)}{x}=1\)
问题的求解——小数的情况:
\(\lim_{x \to 0}\frac{\sin(小数)}{同样的小数}=1\)
\(\lim_{x \to 0}\frac{\tan(小数)}{同样的小数}=1\)
\(\lim_{x \to 0} \cos(小数)=1\)
\(\lim_{x \to 0}\frac{1-\cos(x)}{x}=0\)
第9章 指数函数和对数函数
9.1 基础知识
指数函数:
\(b^0=1\),\(b^1=b\),\(b^x b^y=b^{x+y}\),\(\frac{b^x}{b^y}=b^{x-y}\),\((b^x)^y=b^{xy}\).
对数函数:
\(b^{\log _b (y)}=y\)
对数函数、指数函数及反函数:
\(log_b (b^x)=x\)
对数法则:
\(\log _b(1)=0\),\(\log _b(b)=1\),
\(\log _b(xy)=\log _b(x)+\log _b(y)\),
\(\log _b(x/y)=\log _b(x)-\log _b(y)\),
\(\log _b(x^y)=y\log _b(x)\),
换底法则 \(\log _b(x)=\frac{\log _c(x)}{\log _c(b)}\).
第14章 洛必达法则及极限问题总结
14.1 洛必达法则
洛必达法则类型的总结:

第16章 定积分
done
16.2 定积分的定义
\({\boxed{
\int_{a}^{b} f(x){\rm d}x=\lim_{{\rm mesh\to 0}}\sum_{j=1}^n f(c_i)(x_j-x_{j-1}) }}\)
其中\(a=x_0<x_1<\cdots<x_{n-1}<x_n=b\),并且对于每一个\(j=1,\cdots,n\)都有\(c_j\)在\([x_{j-1}, x_j]\)内。
16.3 定积分的性质
\(\int_{b}^{a} f(x){\rm d}x=-\int_{a}^{b} f(x){\rm d}x\)
\(\int_{a}^{a} f(x){\rm d}x=0\)
\(\int_{a}^{b} f(x){\rm d}x=\int_{a}^{c} f(x){\rm d}x+\int_{c}^{b} f(x){\rm d}x\)
\(\int_{a}^{b} Cf(x){\rm d}x=C\int_{a}^{b} f(x){\rm d}x\)
\(\int_{a}^{b} (f(x)+g(x)){\rm d}x=\int_{a}^{b} f(x){\rm d}x+\int_{a}^{b} g(x){\rm d}x\)
16.4 求面积
在函数\(f\)和\(g\)之间的面积(平方单位)\(=\int_a^b|f(x)-g(x)|{\rm d}x\).
如果存在反函数,\(\int_A^B f^{-1}(y) {\rm d}y\)就是由函数\(y=f(x)\)、直线\(y=A\)和\(y=B\)以及\(y\)轴所围成的面积(平方单位)。
16.5 估算积分
如果对于在区间\([a,b]\)内的所有\(x\)都有\(f(x)\le g(x)\),那么就有\(\int_a^b f(x){\rm d}x \le \int_a^b g(x){\rm d}x\).
如果对于在区间\([a,b]\)内的所有\(x\)都有\(m \le f(x)\le M\),那么\(m(b-a) \le \int_a^b f(x){\rm d}x \le M(b-a)\).
16.6 积分的平均值和中值定理
函数\(f\)在区间\([a,b]\)内的平均值\(=\frac{1}{b-a}\int_a^b f(x){\rm d}x\).
积分的中值定理:如果函数\(f\)在闭区间\([a,b]\)上连续,那么在开区间\((a,b)\)内总有一点\(c\),满足\(f(c)=\frac{1}{b-a}\int_a^b f(x){\rm d}x\).
第17章 微积分基本定理
done
17.2 微积分的第一基本定理

17.3 微积分的第二基本定理

导数和积分公式

17.4 不定积分
如果\(\frac{{\rm d}}{{\rm d}x}F(x)=f(x)\),那么\(\int f(x){\rm d}x=F(x)+C\).
\(\int cf(x){\rm d}x=c\int f(x){\rm d}x\)
\(\int (f(x)+g(x)){\rm d}x=\int f(x){\rm d}x+\int g(x){\rm d}x\)


