写给草履虫的数字信号处理：第1章 信号

目录

1.信号
2.系统
3.傅里叶分析
4.卷积
5.采样
6.离散傅里叶分析
7.快速傅里叶变换
8.频率响应
9.Z-变换
10.滤波器
附录
参考文献

第1章 信号

1.1 信号
1.2 基本连续时间信号
1.3 基本离散时间信号
1.4 基本信号操作
1.5 Matlab示例
（初稿 2022.9.1）

1.1 信号

信号（Signals）是含有一个或多个独立变量函数的数学表示。一个信号描述了一个参数如何随着另一个变化。例如，你的房间里随着时间变化的温度就是一个信号。在一个电路中，随着时间变化的电压也是一个信号。在本书中，我们研究的自变量是时间。

信号有两种基本类型：连续时间信号和离散时间信号。连续时间信号是指那些每时每刻都有定义的信号。离散时间信号则是只有在某些时间才有定义的信号。例如，如果你每一小时读取你房间的温度并画图，则你获取到的是离散时间信号。温度数值只有在整点时刻才有定义，并不是在整个时间轴上都有定义。温度数值在其它时刻（比如半小时或每刻钟）没有被定义。

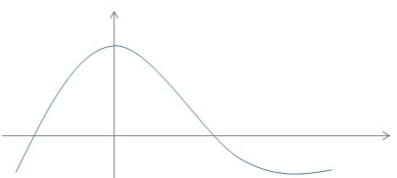
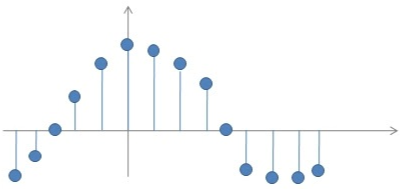
图 1.1-1连续时间变量/离散时间变量

连续时间变量的自变量用\(t\)（时间）表示，离散时间变量的自变量用\(n\)（时刻）表示。因变量分别表示为\(x(t)\)和\(x[n]\)。

1.2 基本连续时间信号

本节我们介绍几种重要的连续时间信号。正确理解这些信号及其行为，将对我们更好地掌握数字信号处理（DSP, Digital Signal Processing）大有帮助。

1.2.1 正弦信号

正弦波和余弦波统称为正弦曲线或正弦信号。
从数学上它们可表示为：

\[x(t)=A\cos (\omega t+\Phi) \tag{1-1} \]

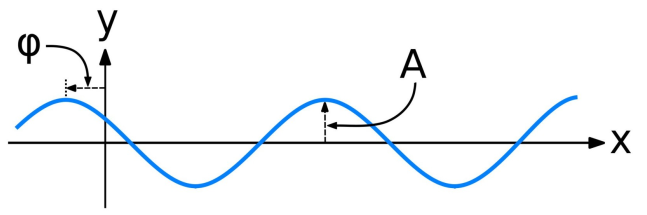
图1.2-1 正弦信号的图像

式\((1-1)\)中\(A\)表示幅度（amplitude）即信号的最大高度，\(\omega\)表示角频率（angular frequency），\(\Phi\)表示相位(phase)。
正弦波和余弦波除了在原点位置不同外（相位角度相差90度），波形基本相同。其时间周期为\(T=2\pi/\omega\)。

借助欧拉公式（Euler's relation），相同（角）频率的正弦与余弦波可以统一表示为复数形式：

\[e^{j\omega t}=\cos(\omega t)+j\sin(\omega t) \tag{1-2} \]

（注：原式有误）这种表示方法使计算容易了许多（虽然一开始看不出来），并且将在本书中广泛采用。

1.2.2 单位阶跃信号

单位阶跃信号的数学定义为：

\[u(t)= \begin{cases} 0, & t<0 \\ 1, & t>0 \end{cases} \tag{1-3} \]

阶跃函数可以想象为一个开关，它在\(t=0\)的时刻开启，之后其输出就维持一个固定的水平。

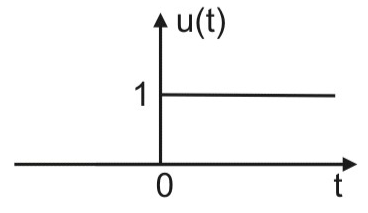
图1.2-2 单位阶跃函数的图像

单位阶跃函数在\(t=0\)时刻是不连续的，但是为了简化处理，取\(u(0)=1\)（一个连续信号不意味着在数学上是一个连续函数）。
单位阶跃函数在控制工程领域具有非常重要的地位。它被用来研究系统的稳态性能。任何阶跃信号都仅是单位阶跃信号的缩放版本。

1.2.3 单位脉冲信号

另一种非常重要的基本信号是单位脉冲信号。其数学定义为：

\[\delta(t)= \begin{cases} 0, & t\neq 0 \\ \infty, & t=0 \end{cases} \tag{1-4} \]

但是，如果单位脉冲函数的值在\(t=0\)处为\(\infty\)，为什么称其为“单位”脉冲函数呢？这是由于在\(t=0\)处，函数具有单位面积1。

考虑一个宽为\(\varepsilon\)、高为\(1/\varepsilon\)的矩形，如图\(1.2-3\)所示。矩形的面积为1。现在将\(\varepsilon\)极小地缩小，并保持面积为1。这清晰地表明，为了保持面积为1，单位脉冲函数在\(t=0\)处将有无穷大的幅度。

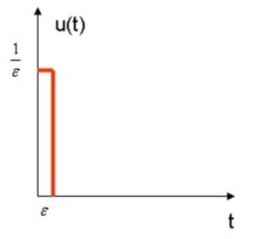
图1.2-3 单位面积的矩形

如图1.2-4所示，箭头的高度用于描述缩放的脉冲，并且表示它的面积。

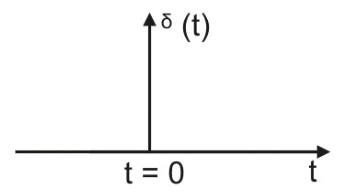
图1.2-4 单位脉冲信号的图像

想像脉冲信号为一个短脉冲，就像一个极速打开并关闭的开关的输出信号。单位脉冲函数也称为德尔塔函数或德尔塔-狄拉克（Delta-Dirac）函数。

单位阶跃信号和单位脉冲信号的关系如下：

\[\frac{d(u(t))}{dt} = \delta(t) \tag{1-5} \]

这个关系是不言自明的。当\(t<0\)时，\(u(t)=0\)，因此斜率为0；当\(t>0\)时，\(u(t)=0\)，因此斜率也为0（注：此处原文为1）；
当\(t=0\)时，\(u(t)\)从0变化为1，因此斜率为\(\infty\)。

关系式\((1-4)\)可重写为积分形式：

\[\int_{-\infty}^{\infty}\delta(t){\rm d}t=u(t) \tag{1-6} \]

即在正负无穷区间对单位脉冲函数进行积分，可得到单位阶跃函数。

1.2.4 指数信号

指数信号是按指数级增长或下降的信号（自然常数\(e\)的幂）。其数学定义为：

\[x(t)={\text C}e^{{\text a}t} \tag{1-6} \]

上式\(e\)是欧拉数（注：也叫自然常数），\({\text C}\)和\({\text a}\)是常数。
指数信号的性质取决于常数\({\text C}\)和\({\text a}\)。如前所述（注：见式\((1-2)\)），指数为复数的指数函数基本上是正弦函数。

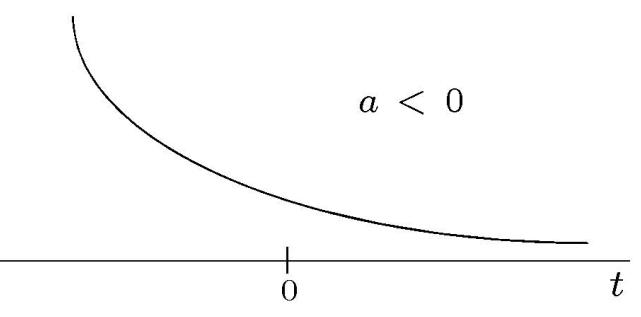
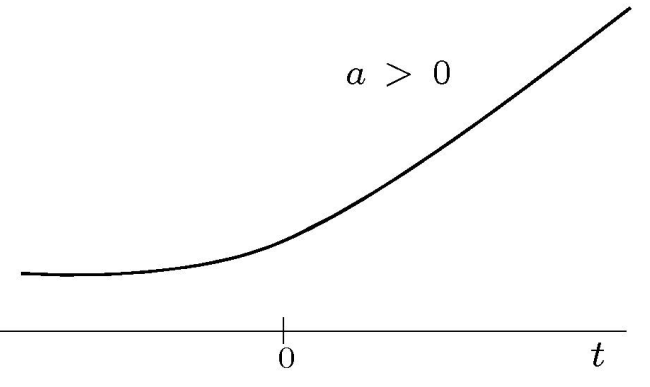
图1.2-5 (a)\(a<0\)的实指数函数，(b)\(a>0的实指数函数\)

另外还有其它的基本函数，如斜坡（ramp）信号，三角（triangular）信号等。但在数字信号处理中，脉冲信号与阶跃信号最为常见。

1.3 基本离散时间信号

上一节讨论过的所有基本连续信号，都有对应的离散信号。让我们快速过一遍。

1.3.1 离散正弦信号

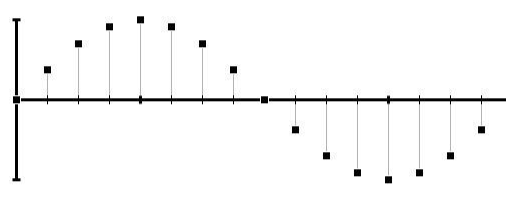
图1.3-1 离散正弦信号

离散正弦信号的数学定义为：

\[x[n]={\text A}\cos (\Omega n+\phi) \tag{1-7} \]

离散正弦信号的所有性质与连续正弦信号相同。

1.3.2 离散单位阶跃信号

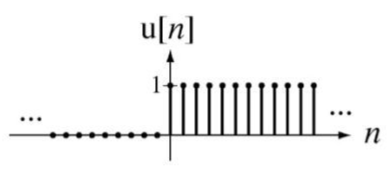
图1.3-2 离散单位阶跃信号

离散单位阶跃信号定义如下：

\[u[n]= \begin{cases} 0, & n<0 \\ 1, & n\ge 0 \end{cases} \tag{1-8} \]

离散单位阶跃信号在\(n=0\)处取值为1。

1.3.3 离散单位脉冲信号

图1.3-3 离散单位脉冲信号

\[\delta[n]= \begin{cases} 0, & n\neq 0 \\ 1, & n=0 \end{cases} \tag{1-9} \]

与连续单位脉冲信号不同，离散单位脉冲信号在\(n=0\)处为有限值。

1.3.4 离散指数信号

离散指数信号定义为：

\[x[n]={\text C}e^{{\text a}n} \tag{1-10} \]

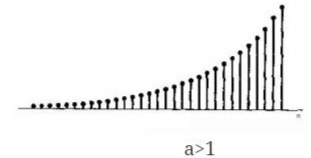
图1.3-4 （a）离散指数信号\(a>0\)

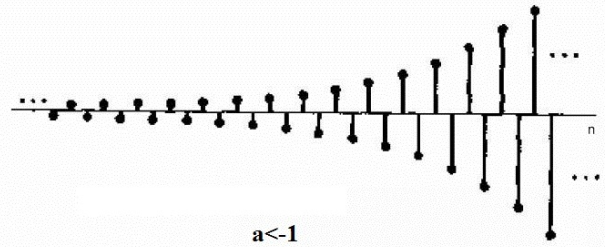
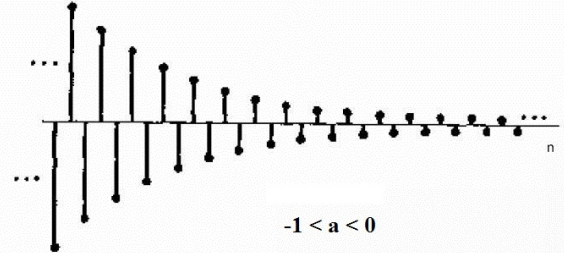
图1.3-4 （b）离散指数信号\(a<0\)

1.4 基本信号操作

一个信号中有两个变量：幅度和时间。通过变化这些参数，我们可以定义一定基本的信号操作。

1.4.1 幅度缩放

幅度缩放就是将幅度乘以一个标量。与幅度相乘的因子可以是任何值。如果该标量大于1，则信号幅度增大，这个处理过程被称为放大。如果该标量小于1，则信号幅度缩小，这个过程过程被称为衰减。

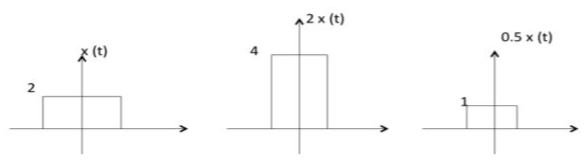
图1.4-1 幅度缩放

幅度缩放可以表示为：\(y(t)={\text a}\ x(t)\)，其中\({\text a}\)为缩放因子。

幅度缩放时，信号在整个定义域中都被缩放。

1.4.2 信号相加

两个或多个信号相加，就是在相同的时刻将它们的幅度相加。
加法（勘误：原文为乘法）操作可以表示为：\(y(t)=x^1(t)+x^2(t)\)

图1.4-2 信号相加

由上图可知：
\(-10<t<-3\)时，信号幅度为：\(z(t)=x^1(t)+x^2(t)=0+2=2\)，
\(-3<t<3\)时，信号幅度为：\(z(t)=x^1(t)+x^2(t)=1+2=3\)，
\(3<t<10\)时，信号幅度为：\(z(t)=x^1(t)+x^2(t)=0+2=2\)。

1.4.3 信号相乘

两个信号相乘，就是在相同的时刻将它们的幅度相乘。
乘法操作可以表示为：\(y(t)=x^1(t) \times x^2(t)\)

图1.4-3 信号相乘

由上图可知，
\(-10<t<-3\)时，信号幅度为：\(z(t)=x^1(t)\times x^2(t)=0\times 2=0\)，
\(-3<t<3\)时，信号幅度为：\(z(t)=x^1(t)\times x^2(t)=1\times2=2\)，
\(3<t<10\)时，信号幅度为：\(z(t)=x^1(t)\times x^2(t)=0\times2=0\)。

1.4.4 时域平移

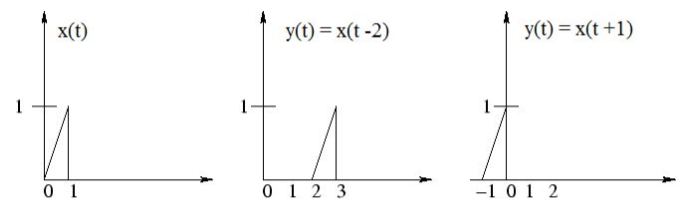
图1.4-4 时域平移

时域平移意味着向前或向后平移信号的起始点。基本上来说，通过时域平移可以快进或延迟一个信号。
时域平移的数学定义如下：\(y(t)=x(t-t_0)\)
以\(y=x(t-2)\)为例。这表示信号会在2个时间单位（注：原文为2秒）后开始，或者被推迟2个时间单位。
考虑另一个例子：\(y(t)=x(t+1)\)。这表示信号会提前1个时间单位开始，或者快进1个时间单位。
如图1.4-4所示。

1.4.5 时域缩放

时域缩放会改变信号的周期，同时保持其幅度不变。简而言之，时域缩放意味着扩展或压缩一个信号且幅度不变。

你试过在音乐播放器上两倍速播放一首歌吗？你是否想知道这是怎么办到的？这确实是可以办到的，因为时域缩放可以精确地压缩时间。你是否注意到这样做音质并不会失真？歌词和播放器都依旧如故，音量也没有增大或减小。这是因为我们没有改变幅度。

时域缩放在数学上可以表示为：\(y(t)=x({\text a}t)\)，其中\({\text a}\)是常数。

当\({\text a}>1\)时，信号被压缩；当\({\text a}<1\)时，信号被扩展。据此来说，信号\(y=x(2t)\)被压缩至一半。这看起来有点奇怪吗？考虑画任意一个图形（比如矩形），将图形分成10小格对应20个单位长度。接下来，再画一个相同的图形，也分成10小格，但对应10个单位长度。
这两个图形有什么差别呢？你会发现图形被压缩了。这正是信号所发生的情况。
注意，一个脉冲函数是不可能进行时域缩放的。

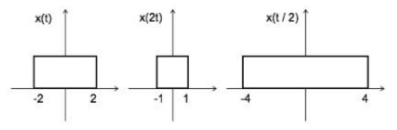
图1.4-5 时域缩放

虽然我们使用连续时间信号来解释信号的操作，但是对离散时间信号来说情况也是一样的。

1.5 MATLAB

1.5.1 基本信号

点击查看Matlab代码

close all;
n = 5;

% 单位脉冲函数
t= -n:1:n; 
y=[zeros(1,n), ones(1,1), zeros(1,n)]; 
subplot(2,2,1); 
stem(t,y); 
ylabel('d(n)'); 
xlabel('unit impulse'); 

% 单位阶跃函数
t=-n:1:n; 
y1=[zeros(1,n), ones(1,1+n)]; 
subplot(2,2,2); 
stem(t,y1); 
ylabel('Amplitude'); 
xlabel('unit step'); 

% 单位爬坡函数
t=-n:1:n; 
subplot(2,2,3);
y1 = t(n+1:end);
y = [zeros(1,n), y1];
stem(t,y); 
ylabel('Amplitude'); 
xlabel('unit ramp'); 

% 指数函数
t=-n:1:n; 
a=2; 
y2=exp(a*t(n+1:end)); 
y = [zeros(1,n), y2];
subplot(2,2,4); 
stem(t,y); 
xlabel('Exponential'); 
ylabel('Amplitude'); 

运行结果如图：

图1.5-1 基本信号

1.5.2 正弦和余弦信号

点击查看Matlab代码

n = 5;
t = -n:1:n;
% 正弦信号
subplot(2,1,1);
y = sin(t);
stem(t,y)
xlabel('n');
ylabel('Amplitude');
title('Sine Signal')

% 余弦信号
subplot(2,1,2);
y = cos(t);
stem(t,y)
xlabel('n');
ylabel('Amplitude');
title('Cosine Signal')

运行结果如图：

图1.5-2 正弦和余弦信号