凸优化学习笔记

学习资源

教材

凸优化.Stephen Boyd.清华大学出版社.2011
参考教材：
最优化：建模、算法与理论.刘浩洋.高等教育出版社.2020
信号处理与通信中的凸优化：从基础到应用.祁忠勇.电子工业出版社 (2021)

MOOC

Stanford.Stephen Boyd

中国科学技术大学.凌青.2011 中科大-凸优化_哔哩哔哩

笔记

《凸优化》中科大-讲解 -系列笔记
凸优化算法与理论@邓康康.知乎
凸优化笔记@周游.知乎
凸优化笔记@Lauer.知乎
凸优化习题选讲@大旗宛成.Bilibili（仅供参考）

CVX 工具箱（安装及用户指南）
Manopt流形优化工具包

经典的SDR算法： 用半正定松弛法 (SDR) 求解二次优化问题

教材笔记

第2章 凸集

基本概念

1 仿射集合 (Affine sets)

\(C \subseteq \mathbf{R}\)是仿射的等价于：对于任意\(x_1\)，\(x_2\in C\)及\(\theta \in \mathbf{R}\)有

\[\theta x_1+(1-\theta)x_2 \in C. \]

\(\textbf{仿射组合}\)：

2 凸集 (Convex sets)

集合\(C\)被称为凸集，如果\(C\)中任意两点间的线段仍然在\(C\)中，即对于任意\(x_1\)，\(x_2\in C\)和满足\(0 \le \theta \le 1\)的\(\theta\)都有

\[\theta x_1+(1-\theta)x_2 \in C. \]

\(\textbf{凸组合}\)：

2 凸锥 (Convex cones)

如果集合\(C\)是锥，并且是凸的，则称\(C\)为凸锥。即对于任意\(x_1\)，\(x_2\in C\)和\(\theta_1, \theta_2 \ge 0\)，都有

\[\theta_1 x_1+\theta_2 x_2 \in C. \]

\(\textbf{锥组合}\)：

重要例子

超平面

半空间

第3章 凸函数

凸函数的定义：
任意\(x, y\in {\text dom}f\)和任意\(0\le \theta\le 1\)，有

\[f(\theta x+(1-\theta)y) \le \theta f(x)+(1-\theta)f(y) \]

一阶条件：

\[f(y)\ge f(x)+\nabla f(x)^T (y-x) \]

二阶条件：

\[\nabla^2 f(x) \succeq 0 \]

第4章 凸优化问题

基本概念

优化问题\(P\)：
优化问题的定义域\(D\)：
优化问题的可行域：属于定义域，且满足约束条件的点\(x\)的集合

基本的规划问题

线性规划LP

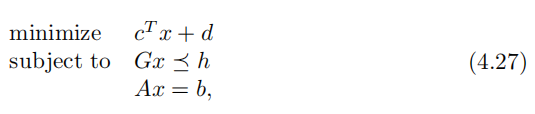
二次规划QP

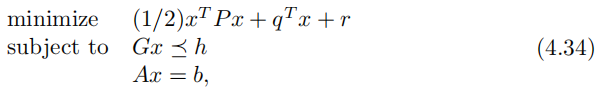
二次约束二次规划QCQP

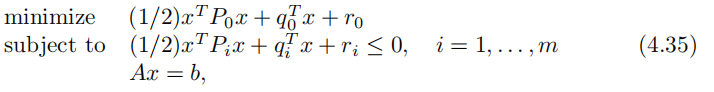
第5章 对偶

鞍点解释：

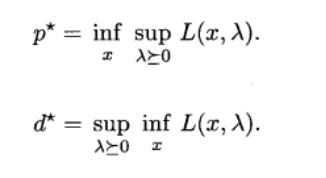
to be continue...

附录

A.有关的数学知识

A.1 范数

向量范数：

L0（\({\cal{l}}_0\)-范数）：向量\(x\)中非0的元素的个数
L1（\({\cal{l}}_1\)-范数）：\(\left\| x \right\|_1 = \left|x_1\right|+\cdots+\left|x_n\right|\)
L2（\({\cal{l}}_2\)-范数/Euclid范数）：\(\left\| x \right\|_2 = (x^Tx)^{1/2} = (x_1^2+\cdots+x_n^2)^{1/2}\)
无穷范数（\({\cal{l}}_\infty\)-范数/Chebyshev范数）：\(\left\| x \right\|_\infty= \max\{\left|x_1\right|, \cdots, \left|x_n\right|\}\)
p范数（\({\cal{l}}_p\)-范数）：\(\left\| x \right\|_p= (\left|x_1\right|^p+\cdots+\left|x_n\right|^p)^{1/p}\)
二次范数：\(\left\| x \right\|^P=(x^T Px)^{1/2} = \left\| P^{1/2}x \right\|_2\)
对偶范数：

矩阵范数：

Frobenius范数：\(\left\| X \right\|_F\)
绝对值之和范数：\(\left\| X \right\|_{\text sav}\)
最大绝对值范数：\(\left\| X \right\|_{\text mav}\)
最大列和范数：\(\left\| X \right\|_1\)
谱范数：\(\left\| X \right\|_2\)
最大行和范数：\(\left\| X \right\|_\infty\)

A.2 分析

上确界（最小上界）：sup\(C\)
下确界（最大下界）：inf\(C\)

D.重要不等式

Cauchy-Schwarz不等式

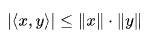
Jensen不等式：
\(f(\theta x+(1-\theta)y) \le \theta f(x)+(1-\theta)f(y)\)

凸优化应用

浅谈多用户通信中总速率优化问题的一些模式