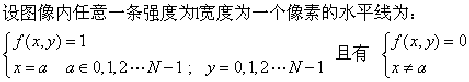我和Fourier有个约会

    回家一个多月，这里杂草丛生。已经两个月没有更新blog，本想继续写paxos的文章，插好键盘开了个头，发现状态全无……想了想还是写傅里叶变换，经过一番深思熟虑后，想出这么俗的一个题目。

    说起和Fourier的结识，那还是在07年的秋天…… 一个对未来充满憧憬的研一傻小子，碰上一个很有实力又特能忽悠的老师——刘XX，不说这两人能擦出火花，最起码是挺合拍的。傻小子稀里糊涂的选了这老师的数字图像处理，这课不用考试，只要在期末的时候做一个presentation。就这样在未来的几个月里，傻小子沉浸在数学的汪洋大海里，和Fourier做了一次亲密接触。

    刘sir上课不喜欢用ppt，一上课就把word打开用MathType插件不停的敲公式。现场推到公式，现场计算积分成为他课上的最大看点。当时是十分震撼的，我的高数在考完研后迅速的还给老师了，怎么能办这些公式记得这么准确！现在看来依然挺厉害的，但不至于到神奇的地步。因为现在理解的所谓的专家就是能重复干某些事上千遍。不过正是这种震撼，让我对数字图像处理产生兴趣，一度想在这个方向深入研究下去，只是后来发现这并不适合我，还发现自己更喜欢网络和分布式。

    数字图像处理不温不火的上了几节课，空间域图像增强一过就进入频率域，接触的第一个变换就是傅里叶变换，傅里叶这位生于1768年的可爱“小卷毛”（如图^_^），在研究热的传播时创立了一套数学理论，他指出任何周期函数都可以表示为不同频率的正弦和/或余弦和的形式，每个正弦和/或余弦乘以不同的系数（现在称为傅里叶级数）。无论函数有多么复杂，只要它是周期的，并且满足默写软的数学条件，都可以用这样的和形式来表示。甚至非周期的函数（函数曲线是有限的情况下）也可以用正弦和/或余弦乘以加权函数的积分来表示。这种情况下公式就是傅里叶变换。傅里叶级数和变换时解决实际问题的工具把较复杂的运算转化为较简单的运算，在信号处理领域产生了巨大的影响。

    正当刘sir在开心的推导fourier级数时，他突然打住很深沉的给我们描述了这样两幅图像：如果一幅图像中只有一条直线(如下图)

 

那么经过傅里叶变换后得到的频谱图会是什么样的呢？（变换后图像如下图，图像没有进行坐标移动）

 

可以发现一个奇怪的现象，原图像的直线“好像”和变换后的频谱图中的直线垂直！这两条直线真的垂直吗？如果垂直，这又是为什么呢？频谱图中的值表示的是傅里叶变换结果的模值的大小，如果是垂直的，也就是说图像中大部分能量集中在与原图垂直的方向的频率上，那么这又表示出什么样的物理意义呢？

    听了这些，我又热血沸腾了，这不就是一个论文题目吗？这课的课程设计不就有了吗！真是不知天高地厚。开始动手以后才发现有多困难，一个月的时间查了所有能查的资料，包括网站、书、中英文论文，竟没有一篇文文章直接证明或者介绍这个现象，不过值得欣慰的是有几篇英文文献里用到这个垂直的性质，但都是一笔带过，没有做介绍，更没有证明。难道这东西没有证明的价值？还是大家都觉得这东西不需要证明呢？和朋友们聊天是聊到这个事，其中一位泼我冷水说“这可能就是一个公理不需要证明”。这么一说感觉挺有理的，但这个现象是由fourier变换后产生的，应该是有其中的奥妙的。于是在连续两个月的时间里，闲着没事的我开始习惯性逃掉所有觉得“没用”的课，每天上自习看文献、对着Fourier公式发愣。这段时间是快乐的，因为除了Fourier什么都不用想，什么都不管，就像回到高三，原来专心学习是这么幸福。看的书越来越多，对Fourier变换的理解也慢慢加深，越发觉得这些公式是如此漂亮，这些数学家是如此的不可思议。在多位学长和数学学院的同学的帮助下终于给出这个垂直现象的数学证明，其中还加入我对物理意义的一些理解。期末的presentation很顺利，刘sir给了我一个最高分，也让我得意了一阵子。不过后来偷懒了，没有将这篇论文正式发表。

    下面给出水平直线段垂直现象的证明，这是论文的一部份。在论文中还给出斜线段垂直现象的证明以及物理意义的理解，想看完整版的同学请点这里：我是完整版 ，这里还有presentation时的ppt：我是ppt

 

论文内容：本节给出只由一条直线段组成的图像的数学证明，在4.1中给出对图像内任意一条水平的直线段的证明，在4.2节中给出任意一条斜线段的证明。

因为频谱图中的灰度代表傅立叶变换的模值，因此证明变换前后出现垂直现象，实际上就是求傅立叶变换后模将会在什么位置或者说什么方向上出现最大值。即讨论求模公式：

的最大值将出现在的什么方向上。

4.1水平直线段垂直现象的证明

设输入图像为一个的二维矩阵，图像内任意一条水平直线段定义如下：

带入（1）式可得：

由（2）式可以看出，模的值只可能出现在的一列或者多列，也就是说在变换后的频谱图里亮线可能出现在垂直的方向上，这就很好的证明了图3.3(b)中出现的垂直现象。但是（2）式并不能说明模值只出现在这一列，因此还要对（2）式进行进一步的讨论。

如果把（2）式中的连加看成是对积分的取样，并把扩充到，则可以得到如下的（3）式，并对其计算可得以下的等式：

 

    费了这么大的劲，写了这么多公式，工程师们肯定会问：这东西有什么用？(阿里研究院一面的帅哥就是这样问我的)其实说实话刚开始我也不知道有什么用，只是觉得好玩。后来又看了些文献，发现有了这个性质以后对一些有规律噪声的图像，比如印刷品扫描后的图像容易出现规律性噪声，专业点的Moir´e Effects、 periodic layer、Regular patterns等都可以转成Fourier Spectrum后用这个垂直性质来“Detect”。

    下面几张图片来自冈萨雷斯的《Digital Image Processing Third Edition》的第四章的ppt，可以看到小冈同学也用这个性质来去噪。