软工第三次作业——最大子段和的求解
一、问题描述
给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
--引用自《百度百科》
二、问题分析
1.求最大子段和算法分析
整型变量Max作为序列s[]的长度,定义数组Sum[]保存s[Max]各个元素的累加值,即最大子段和的候选值序列,underzero记录序列s[]中小于等于0的元素的个数,定义MAXSUM为最大子段和,若underzero=Max,即如果序列s[]中的元素均小于等于0,输出最大子段和为0;否则的话给MAXSUM赋初值Sum[0];然后和Sum[]中的其他元素比较;若MAXSUM<=Sum[i];则将Sum[i]赋值给MAXSUM,这样就得到了序列s[]的最大子段和。
2.算法流程图

三、代码编写
package themax;
import java.util.Scanner;
public class TheSumMax {
public static int SumMax(int Max,int s[]) {
int i;
//Sum[]数组保存的是s[Max]各个元素的累加值,即最大子段和的候选值
int[] Sum = new int[255];
int max = 0;
//underzero记录的是s[Max]中小于等于0的元素的个数,若都是小于等于0的元素输出最大子段和为0
int underzero = 0;
for(i = 0;i < Max;i ++) {
Sum[max] = s[i];
if(s[i] <= 0) {
underzero ++;
}
max ++;
for(int j = i + 1;j < Max;j ++) {
Sum[max] = Sum[max-1] + s[j];
max ++;
}
}
//MAXSUM为最大子段和
int MAXSUM;
if(underzero == Max)
MAXSUM = 0;
else {
MAXSUM = Sum[0];
for(i = 1;i < max;i ++) {
if(MAXSUM < Sum[i])
MAXSUM = Sum[i];
}
}
return MAXSUM;
}
public static void main(String[] args) {
Scanner scan1 = new Scanner(System.in);
int n = scan1.nextInt();
int [] sum = new int[n];
Scanner scan2 = new Scanner(System.in);
for(int i = 0; i < n; i ++) {
sum[i] = scan2.nextInt();
}
System.out.println(SumMax(n,sum));
}
}
四、语句覆盖测试
1.判定/条件覆盖方法
该语句覆盖测试方法要求设计足够多的测试用例,使得判定中每个条件的所有可能结果至少出现一次,每个判定本身所有可能结果也至少出现一次。。
2.判断条件分析及测试用例的设计
根据代码和流程图不难发现判断条件i < Max, j=i+1 < Max , i< max, 均为循环判定条件,即不管是什么测试用例,都会满足这三条判断条件的任何一种情况,所以我们设计的测试用例只需要能够覆盖s[i] <= 0,underzero = Max,MAXSUM <=Sum[i] 这三条判定条件就可以了。故设计了两条测试用例:(1)n = 4,sum[n] = {2,1,4,3} (2)n = 4,sum[n] =
3.测试代码及运行结果
(1)n = 4,sum[n] =
测试代码
package themax;
import static org.junit.jupiter.api.Assertions.*;
import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.Test;
class TheSumMaxTest {
@BeforeEach
void setUp() throws Exception {
}
@Test
void testSumMax() {
int Max = 4;
int[] s = {1,2,3,4};
}
@Test
void testMain() {
int n = 4;
int[] sum = {2,1,4,3};
assertEquals(10,new TheSumMax().SumMax(n, sum));
}
}
运行结果
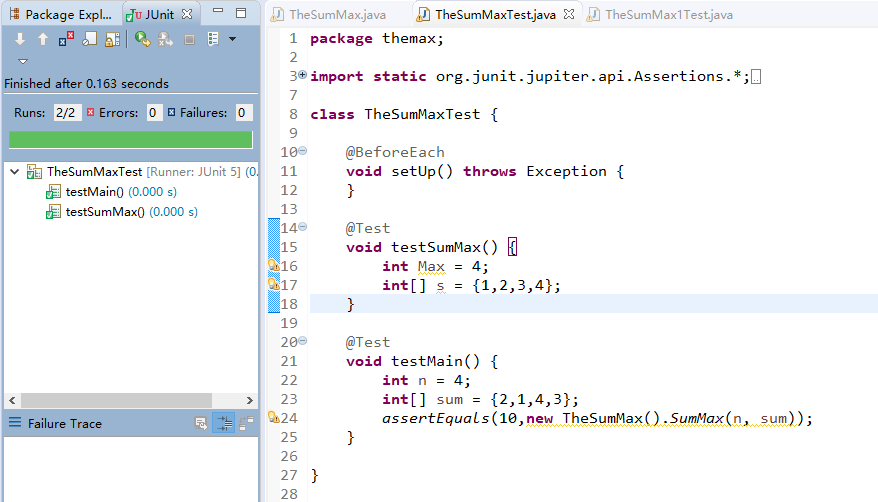
(2)n = 4,sum[n] =
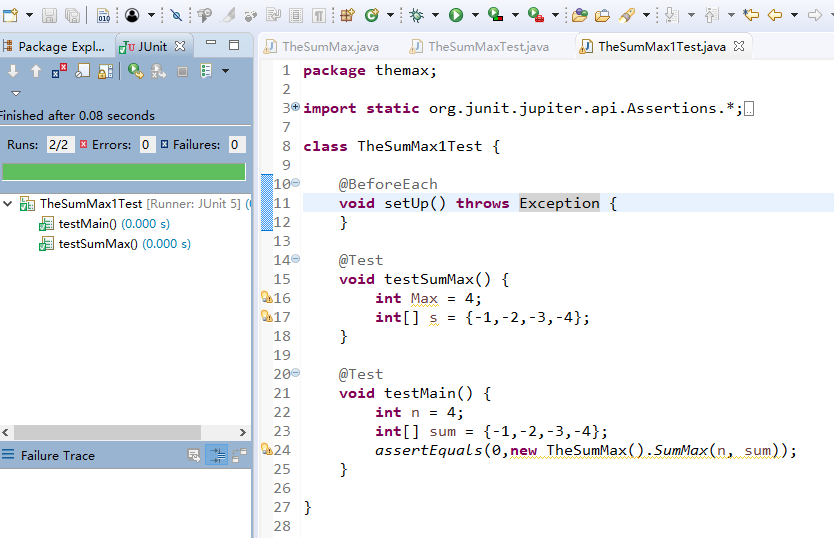
测试代码
package themax;
import static org.junit.jupiter.api.Assertions.*;
import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.Test;
class TheSumMax1Test {
@BeforeEach
void setUp() throws Exception {
}
@Test
void testSumMax() {
int Max = 4;
int[] s = {-1,-2,-3,-4};
}
@Test
void testMain() {
int n = 4;
int[] sum = {-1,-2,-3,-4};
assertEquals(0,new TheSumMax().SumMax(n, sum));
}
}
运行结果