排序算法
排序一:直接插入排序
每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍然有序。
1、第一趟比较前两个数,然后把第二个数按大小插入到有序表中;
2、第二趟把第三个数据与前两个数从前向后扫描,把第三个数按大小插入到有序表中;
3、依次进行下去,进行了(n-1)趟扫描以后就完成了整个排序过程。
直接插入排序属于稳定的排序,最坏时间复杂度为O(n^2),空间复杂度为O(1)。
下面按从小到大排序:
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; insert_sort(data); showData(data); } //打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.println(data[i]); } } // 直接插入排序 private static void insert_sort(int[] data) { int t; int j; for (int i = 1; i < data.length; i++) {// i表示插入次数,共进行data.length-1次插入 t = data[i];// 把待排序元素赋给t j = i-1; while ((j >= 0) && (t < data[j])) { data[j+1] = data[j]; j--; }// 顺序比较和移动 data[j+1] = t; } } }
排序二:折半插入排序
折半插入排序是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
具体操作:在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为a[high],则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小,则选择a[low]到a[m-1]为新的插入区域(即high=m-1),否则选择a[m+1]到a[high]为新的插入区域(即low=m+1),如此直至low<=high不成立,即将此位置之后所有元素后移一位,并将新元素插入a[high+1]。
下面按从小到大排序:
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; binarySearchInsertion(data); showData(data); } //打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.println(data[i]); } } private static void binarySearchInsertion(int data[]) { int middle = 0; for (int i = 1; i < data.length; i++) { int low = 0; int high = i - 1; int t = data[i]; while (low <= high) { middle = (low + high) / 2; if (t < data[middle]) { high = middle - 1; }else { low = middle + 1; } } for (int j = i; j > middle; j--) { data[j] = data[j-1]; } data[high + 1] = t;// 此处用data[low] = t;也可 } } }
序列:
31 23 89 10 47 68 8 22
i = 1: 23 31 89 10 47 68 8 22
i = 2: 23 31 89 10 47 68 8 22
i = 3: 10 23 31 89 47 68 8 22
i = 4: 10 23 31 47 89 68 8 22
i = 5: 10 23 31 47 68 89 8 22
i = 6: 8 10 23 31 47 68 89 22
i = 7: 8 10 22 23 31 47 68 89
这样数组从小到大就排序好了。
排序三:希尔排序
希尔排序(Shell Sort)是插入排序的一种。是针对直接插入排序算法的改进。该方法又称缩小增量排序
基本思想:先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
从小到大排序:
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; shell(data); showData(data); } //打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] +" "); } } // 希尔排序 private static void shell(int data[]) { int k = data.length / 2;// k值代表前文中的增量d值 , 一般的初次取序列的一半为增量,以后每次减半,直到增量为1 int j; while (k >= 1) {// 当增量k值变化到0,结束循环…… int t; for (int i = k; i < data.length; i++) { t = data[i]; j = i - k; while ((j >= 0) && (t < data[j])) { data[j + k] = data[j]; j = j - k; } data[j + k] = t; } k = k / 2; } } }
序列:
31 23 89 10 47 68 8 22
31 23 89 10 47 68 8 22
31 23 89 10 47 68 8 22
31 23 8 10 47 68 89 22
31 23 8 10 47 68 89 22
8 23 31 10 47 68 89 22
8 10 31 23 47 68 89 22
8 10 31 23 47 68 89 22
8 10 31 23 47 68 89 22
8 10 31 23 47 68 89 22
8 10 31 22 47 23 89 68
8 10 31 22 47 23 89 68
8 10 31 22 47 23 89 68
8 10 22 31 47 23 89 68
8 10 22 31 47 23 89 68
8 10 22 23 31 47 89 68
8 10 22 23 31 47 89 68
8 10 22 23 31 47 68 89
最后排序也就出来了。
排序四:冒泡排序
冒泡排序算法:
1、比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
3、针对所有的元素重复以上的步骤,除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; bubbleSort(data); showData(data); } // 打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + " "); } } // 冒泡排序 private static void bubbleSort(int[] data) { boolean exchange;// 交换标志 int t; for (int i = 1; i < data.length; i++) {// 最多做n-1趟排序 exchange = false;// 本趟排序开始前,交换标志应为假 for (int j = 1; j <= data.length - i; j++) { // 对当前无序区R[i..n]自下向上扫描 if (data[j] < data[j - 1]) {// 交换记录 t = data[j]; // t仅做暂存单元 data[j] = data[j - 1]; data[j - 1] = t; exchange = true; // 发生了交换,故将交换标志置为真 } } if (!exchange) {// 本趟排序未发生交换,提前终止算法 return; } } } }
排序五:快速排序
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
下面从小到大排序:
public class Sort { public static void main(String[] args) { int[] data = { 31, 23, 89, 10, 47, 68, 8, 22 }; quickSort(data, 0, data.length - 1); showData(data); } // 打印数组 private static void showData(int[] data) { for (int i = 0; i < data.length; i++) { System.out.print(data[i] + " "); } } // 快速排序 private static void quickSort(int[] data, int low, int high) { // 对data[low..high]快速排序,low,high表示下标数 int k; // 划分后的基准记录的位置 if (low < high) { // 仅当区间长度大于1时才须排序 k = quickPass(data, low, high); // 对R[low..high]做划分 quickSort(data, low, k - 1); // 对左区间递归排序 quickSort(data, k + 1, high); // 对右区间递归排序 } } private static int quickPass(int data[], int i, int j) { int t = data[i]; // 用区间的第1个记录作为基准 while (i < j) { // 从区间两端交替向中间扫描,直至i=j为止 while (i < j && data[j] >= t) { // t相当于在位置i上 j--; // 从右向左扫描,查找第1个关键字小于t的记录data[j] } if (i < j) { // 表示找到的data[j]的关键字<t data[i++] = data[j]; // 相当于交换data[i]和data[j],交换后i指针加1 } while (i < j && data[i] <= t) { // t相当于在位置j上 i++; // 从左向右扫描,查找第1个关键字大于t的记录data[i] } if (i < j) { // 表示找到了data[i],使data[i]>t data[j--] = data[i]; // 相当于交换data[i]和data[j],交换后j指针减1 } } data[i] = t; // 基准记录已被最后定位 return i; } }
序列:
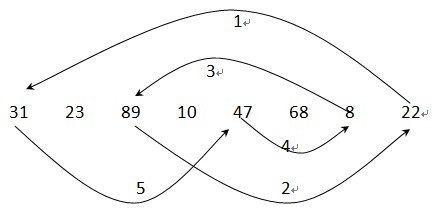
交换后:22 23 8 10 31 68 47 89
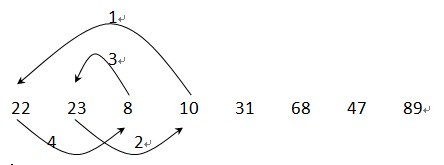
交换后:10 8 22 23 31 68 47 89
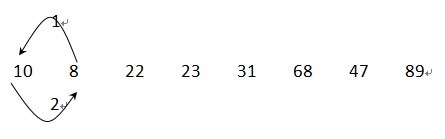
交换后:8 10 22 23 31 68 47 89

交换后:8 10 22 23 31 47 68 89
最后快速排序就结束了,从小到大为:8 10 22 23 31 47 68 89 。




