软工个人作业
| 项目 | 内容 |
|---|---|
| 课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求 | 个人项目作业 |
| 教学班级 | 006 |
| 项目地址 | https://github.com/17373380/Personal |
PSP项目表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 5 | 5 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 30 |
| · Design Spec | · 生成设计文档 | 20 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 60 | 90 |
| · Coding | · 具体编码 | 100 | 120 |
| · Code Review | · 代码复审 | 20 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 80 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| . | 合计 | 395 | 465 |
解题思路
拿到题目后分析,有两种数据类型,直线和点。
直线常见的表示形式有:
- 一般式:Ax+By+C=0(A、B不同时为0)【适用于所有直线】
- 点斜式:y-y0=k(x-x0) 【适用于不垂直于x轴的直线】
- 截距式:x/a+y/b=1【适用于不过原点或不垂直于x轴、y轴的直线】
- 斜截式:y=kx+b【适用于不垂直于x轴的直线】
- 两点式:(y-y1)/(y2-y1)=(x-x1)/(x2-x1) (x1≠x2,y1≠y2)【适用于不垂直于x轴、y轴的直线】
其中直线我选用ax+by+c=0的标准方程来表示,此方程可以表示平行于x轴或者平行于y轴的直线,不用特殊考虑。点再一开始我准备使用(x,y)坐标的方法来表示,但再实际操作之后发现:交点坐标绝大部分是小数,而其精度的确定成了难题,有可能依照不慎,满盘皆输。所以在细致考虑后决定使用分数来表示坐标。
输入的数据时按行排列的,所以我就按行读取,再用空格进行分割,得到原始数据,解方程求得直线ax+by+c=0。每加入一条新直线就与之前的所有直线求解交点。
设计实现过程
主要函数
| 函数名 | 作用 |
|---|---|
| int str2int(string now) | 将string转化为int型。 |
| void Container::getNewCross(Line *nline) | 求解新直线与已有直线的交点。 |
| Cross::Cross(Line *line1, Line *line2) | 求两直线的交点。 |
| Line::Line(int x1, int y1, int x2, int y2) | 根据两点求解直线。 |
我计划构建三个类:Line,Cross,Container,分别是直线,交点和存放二者的容器。
class Line {
public:
int a;
int b;
int c;
Line(int x1, int y1, int x2, int y2);
~Line();
void printLine();
string line2str();
};
class Cross {
public:
int numX;
int denX;
int numY;
int denY;
Cross(Line *line1, Line *line2);
~Cross();
bool operator ==(const Cross&) const;
bool operator >(const Cross&) const;
bool operator <(const Cross&) const;
void printCross();
};
class Container {
public:
vector<Line*> *lineSet = new vector<Line*>(); //= new set<Line>();
set<Cross> *crossSet = new set<Cross>();
Container();
~Container();
void addLine(Line *line);
void getNewCross(Line *nLIne);
int getCrossNum();
void printLineSet();
void printCrossSet();
};
存放直线与交点的数据结构分别用vector和set
vector<Line*> *lineSet = new vector<Line*>();
set<Cross> *crossSet = new set<Cross>();
在读入直线的数量N后,进行N次循环,每次循环将新获得的直线与已有直线求解交点,并将新交点和新直线加入到容器中。
for (i = 0; i < lines; i++) {
in >> type;
if (type == "L") {
in >> x1 >> y1 >> x2 >> y2;
Line *tempLine = new Line(x1, y1, x2, y2);
container.getNewCross(tempLine);
}
}
求解直线,只需用简单的数学知识即可。
Line::Line(int x1, int y1, int x2, int y2) {
if (x1 == x2) {
this->a = 1;
this->b = 0;
this->c = -x1;
}
else if (y1 == y2) {
this->a = 0;
this->b = 1;
this->c = -y1;
}
else {
this->a = y2 - y1;
this->b = x1 - x2;
this->c = y1 * x2 - y2 * x1;
}
}
循环直线容器求解交点。
Cross::Cross(Line *line1, Line *line2) {
this->numX = line1->c * line2->b - line2->c * line1->b;
this->denX = line1->b * line2->a - line2->b * line1->a;
this->numY = line1->a * line2->c - line2->a * line1->c;
this->denY = this->denX;
if (this->numX < 0 && this->denX < 0) {
this->numX = -this->numX;
this->denX = -this->denX;
}
if (this->numY < 0 && this->denY < 0) {
this->numY = -this->numY;
this->denY = -this->denY;
}
}
最后获取交点个数
container.getCrossNum();
单元测试的构造
单元测试主要偏重于对边界数据以及特殊情况的构造(直线平行或相交于一点)。
TEST_METHOD(TestMethod8)
{
Line* line1 = new Line(0, 0, 99998, 2);
Line* line2 = new Line(0, 2, 49999, 3);
Assert::IsTrue(parallel(*line1, *line2));
}
TEST_METHOD(TestMethod11) {
Line* line1 = new Line(0, 0, 0, 1);
Line* line2 = new Line(0, 0, 1, 0);
Line* line3 = new Line(0, 0, 1, 1);
Line* line4 = new Line(0, 1, 1, 1);
Container container;
container.getNewCross(line1);
container.getNewCross(line2);
container.getNewCross(line3);
container.getNewCross(line4);
Assert::AreEqual(3, container.getCrossNum());
}
性能分析
-
cpu使用
对1000条直线计算

-
函数分配
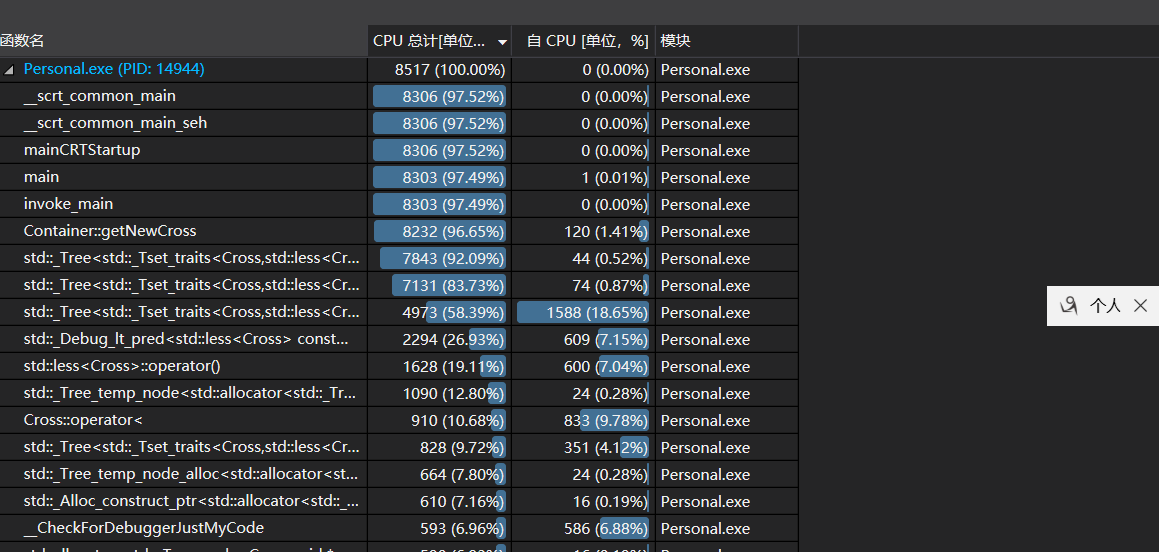
大部分操作都是set树的操作。 -
性能改进
对set的operator判断进行了改进,
原来将直线全部读入之后再计算交点,改进后读入一条新直线,就计算好交点。


