[ABC267F] Exactly K Steps题解

[ABC267F] Exactly K Steps

题意

有一颗 \(n\) 个点，\(n - 1\) 条边的树，找到任意一个离结点 \(u\) 的距离恰好为 \(k\) 的点，或报告无解。

定义两点 \(u, v\) 间的距离为这两个点之间的最短路径所包含的边数。

思路

考虑无解，显然如果从 \(u\) 走出来的最长简单路径的长度都没有 \(k\) 大，那么肯定无解，我们还知道树中任意一个点的最长路径的终点肯定是这棵树的直径的端点中的一个，那么可以推出来这么一个图，表示任意一个点的答案可能出现的地方（用红色圈起来）：

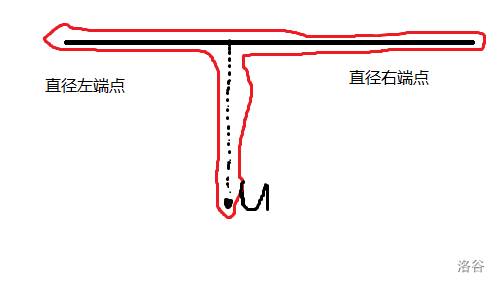
于是可以离线处理，记录从点 \(u\) 搜到直径两端的路径，再记录答案，一个一个的搜肯定会 TLE，所以可以从直径两端开始搜。

代码

#include <iostream>
#include <vector>

using namespace std;

const int MaxN = 2e5 + 10;

struct S {
  int x, y;

  bool operator<(const S &j) const {
    return y < j.y;
  }
};

int u[MaxN], k[MaxN], ans[MaxN], n, q;
vector<int> g[MaxN], c;
vector<S> l[MaxN];

S dfs(int x, int fa) {
  S res = {x, 0};
  for (int i : g[x]) {
    if (i == fa) {
      continue;
    }
    res = max(res, dfs(i, x));
  }
  return {res.x, res.y + 1};
}

void DFS(int x, int fa) {
  c.push_back(x);
  for (int i : g[x]) {
    if (i == fa) {
      continue;
    }
    DFS(i, x);
  }
  int len = c.size();
  for (S i : l[x]) {
    (len > i.x) && (ans[i.y] = c[len - i.x - 1]);
  }
  c.pop_back();
}

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1, u, v; i < n; i++) {
    cin >> u >> v;
    g[u].push_back(v);
    g[v].push_back(u);
  }
  cin >> q;
  for (int i = 1; i <= q; i++) {
    cin >> u[i] >> k[i];
    l[u[i]].push_back({k[i], i}), ans[i] = -1;
  }
  int lres = dfs(1, -1).x, rres = dfs(lres, -1).x;
  DFS(lres, -1), DFS(rres, -1);
  for (int i = 1; i <= q; i++) {
    cout << ans[i] << '\n';
  }
  return 0;
}