数学集
向量
(有方向的值叫做向量)
定义?
这个东西放在平面直角坐标系里会好理解一些所以开始吧:
向量是有一个起点
向量是可以平移的,由于平移,那么起点与终点坐标之差是不变的,所以移动向量,向量的值也不便。
那么放在平面直角坐标系时,我们可以把起点就设为原点,那么这个向量的值就将会是终点的坐标,相当于是将其平移,使起点与原点重合。
计算?
向量加法
课本里有一个三角形法则平行四边形法则,我感觉没有必要,因为两个向量相加,我们可以看成一个点的移动,由于已经放入了平面这叫坐标系,那么我们的移动方向其实就是移动值的正负,于是先按照第一条向量的长度要求来移动,再按照第二个向量的长度要求来移动即可。
向量数乘
(别问我减法呢?)
数乘指的是一个数乘一个向量,相当于是一堆这个向量相加,所以将向量的每个值乘一个要乘的数即可。
那么一个向量的相反向量,即往相反方向走,既是将向量乘一个
向量减法
与其做减法,不如做加法,直接将减数乘
点积(数量积)
定义为:
我们有:
在平面直角坐标系中,两向量
设一个平面直角坐标系,将两个单位设为
叉积(我终于不知道这个东东叫个啥了)
定义为:
在平面直角坐标系中,两向量
设一个平面直角坐标系,将两个单位设为
叉积求面积
这里只用三角形做示范,因为其它的都可以被分成一堆的三角形。
有三角形
面积公式中有一个为底乘高除二,然后找到一个点
康托展开
对于
理解:由排列映射到排名可以视为一种哈希。
原理:设有
卡特兰数
是一种数列,其通项公式的一种形式为:
另一种为:
递归定义式
理解:对于
使用场景
递归式
例1. 01 排列问题
给定
起点左下角
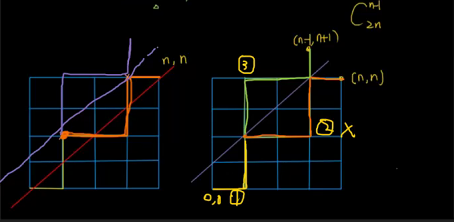
与
将原路径第一次接触新对角线(紫色)之后的路径沿新对角线反转,则原路径与以
那么求原路径中的非法路径数量等价于求以
例2. 给定
例3. 给定
例4. 给定
是一种树形结构与序列相互映射的规则。
区别
欧拉序
二叉搜索树
如何得到
- 统计树上所有结点的度数
- 找到所有度数为
- 令序列
- 重复
void to_p() { int k; for (int i = 1; i <= n; i++) { if (deg[i] == 1) { k = i; break; } } for (int i = 1, j = k; i <= n - 2; i++) { int nf = fa[j]; p[i] = nf; deg[nf]--; if (deg[nf] == 1 && nf < k) { j = nf; continue; } for (k++, j = k; deg[k] != 1; k++, j = k) { } } }
性质
- 结点
- 编号最大的点
- 对于
- 对于
- 对于
- 对于
还原
void to_t() { for (int i = 1; i <= n; i++) { deg[i]++, deg[p[i]]++; } int k, cnt = 0, j; for (int i = 1; i <= n; i++) { if (deg[i] == 1) { k = j = i; break; } } for (int i = 1; i <= n - 2; i++) { int nf = fa[j] = p[i]; deg[nf]--; if (deg[nf] == 1 && nf < k) { j = nf; continue; } for (k++, j = k; deg[k] != 1; k++, j = k) { } } fa[j] = n; }
基本计数原理
- 加法原理:解决一件事情,有
- 乘法原理:解决一件事情,有
排列与组合
- 排列:将
- 组合:将
多重集的排列数与组合数
多重集排列数是指
多重集组合数 1:
设有
组合数常用性质
二项式定理
组合数计算
- 杨辉三角递推计算
- 定义式计算
错位排序
有
- 若前面的已错位排序,那么只要将当前的与之前的换一下即可:
- 若前面恰好有一个没错位,那么只要将当前的与前面的换一下即可:
- 若都不满足,一次操作必然不可能使它错位,所以贡献为
所以
卢卡斯定理
对于正整数
变式
设
费马小定理
若
-
那么
-
记作:
位运算的一个定理
线性计算逆元的小技巧:
设:
所以可以递推求解,对于
首先可以将式子拆成:
首先式子需要一个
那么此时
然后以此类推……
到最后便成了
所以可以扩展
本文作者:yabnto
本文链接:https://www.cnblogs.com/ybtarr/p/17410204.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步