201871030134-余宝鹏 实验二 个人项目一 《D{0-1}KP》项目报告

项目
内容
课程班级博客链接 班级博客
这个作业要求链接 作业要求
我的课程学习目标 1、掌握软件项目个人开发流程
2、掌握Github发布软件项目的操作方法
这个作业帮助我在哪些方面实现学习目标 1、通过阅读都《构建之法》前2章，掌握PSP流程
2、通过开发项目D{0-1}KP掌握软件项目个人开发流程
3、通过提交个人软件项目到Github，掌握Github发布软件项目的操作方法
项目Github的仓库链接地址 Github仓库链接

任务1的作业点评链接

任务2：PSP流程

个人软件过程（PSP）

  • 中文名 个人软件过程
    外文名 Personal Software Process
    简称 PSP
    作用 确定过程的改变 影响

  • 含义：个人软件过程(Personal Software Process，PSP)是一种可用于控制、管理和改进个人工作方式的自我持续改进过程，是一个包括软件开发表格、指南和规程的结构化框架。PSP与具体的技术（程序设计语言、工具或者设计方法）相对独立，其原则能够应用到几乎任何的软件工程任务之中。PSP能够说明个体软件过程的原则； 帮助软件工程师作出准确的计划；确定软件工程师为改善产品质量要采取的步骤；建立度量个体软件过程改善的基准；确定过程的改变对软件工程师能力的影响。

  • 具体运用：在下面的任务中，使用PSP来展示自己对于任务的估计以及实际消耗时间，以此对于软件工程个人项目开发有更为深刻的认识。

任务3：个人软件项目开发

  • 项目开发背景：D{0-1}KP是经典{0-1}背包问题的一个拓展形式，用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解，达到获利最大化。

    D{0-1}KP数据集由一组项集组成，每个项集有3项物品可供背包装入选择，其中第三项价值是前两项之和，第三项的重量小于其他两项之和，算法求解过程中，如果选择了某个项集，则需要确定选择项集的哪个物品，每个项集的三个项中至多有一个可以被选择装入背包，D{0-1} KP问题要求计算在不超过背包载重量C的条件下，从给定的一组项集中选择满足要求装入背包的项，使得装入背包所有项的价值系数之和达到最大。

    D{0-1} KP instances数据集是研究 D{O-1}背包问题时，用于评测和观察设计算法性能的标准数据集；动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。

  1. 需求分析

    • 算法要求：动态规划算法、回溯算法
    • 程序要求：查阅相关资料，设计一个采用动态规划算法、回溯算法求解D{0-1}背包问题的程序
    • 技术要求：需要掌握动态规划算法和回溯算法，要对0-1背包问题熟练掌握，要学会数据可视化技术以及python的切片，保存数据到文本等操作
    • 语言要求：项目未规定语言，所以在解决过程中可使用学过的编程语言。项目要求对数据进行读取以及数据可视化，故初步设想使用python语言实现。

  2. 功能设计

    • 1.可正确读入实验数据文件的有效D{0-1}KP数据；
    • 2.能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图；
    • 3.能够对一组D{0-1}KP 数据按项集第三项的价值:重量比进行非递增排序；
    • 4.用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间（以秒为单位）；
    • 5.任意一组D{0-1}KP数据的最优解、求解时间和解向量可保存为txt文件或导出 EXCEL文件。

  3. 设计实现

    说明：对于D{0-1}KP问题，我未能在实验中将其解决，实验时遇到的问题首先是对于数据的切片读取，我在实验过程中查找了很多资料，知网上有不同于动态规划和回溯算法的解决算法，我阅读了几篇论文，但是这些算法太过高深，我未能理解。因此，我将0-1背包问题进行了深一步的学习，具体内容如后面博客。

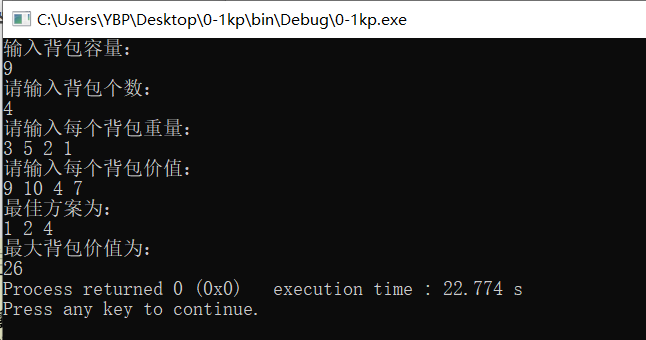
    问题描述：有5个物品，其重量分别是{2, 2, 6, 5, 4}，价值分别为{6, 3, 5, 4, 6}，背包的容量为10，计算背包所能装入物品的最大价值。

    ​ 动态规划算法：在0/1背包问题中，物品i或者被装入背包，或者不被装入背包，设xi表示物品i装入背包的情况，则当xi=0时，表示物品i没有被装入背包，xi=1时，表示物品i被装入背包。根据问题的要求，有如下约束条件和目标函数：

    \[\begin{cases} \sum_{1}^{n}{W_iX_i}\leq{C}\\ X_i\epsilon\big\{0,1\big\},(1\leq{i}\leq{n})\end{cases} \]

    \[max\sum_{i=1}^{n}{V_iX_i} \]

    ​ 于是，问题归结为寻找一个满足约束条件式1，并使目标函数式2达到最大的解向量X=(x1, x2, …, xn)。0/1背包问题可以看作是决策一个序列(x1, x2, …, xn)，对任一变量xi的决策是决定xi=1还是xi=0。按下述方法来划分阶段：第一阶段，只装入前1个物品，确定在各种情况下的背包能够得到的最大价值；第二阶段，只装入前2个物品，确定在各种情况下的背包能够得到的最大价值；依此类推，直到第n个阶段。

    ​ 用回溯算法解决时主要注意以下几点：

    1. 如何建立解空间树
    2. 如何进行剪枝
    3. 是否需要达到最优

  4. 测试运行

    运行截图（动态规划算法）：

    运行截图（回溯算法）：

  5. 代码片段

    • 动态规划算法

      int KnapSack(int n, int w[], int v[]){
	int i, j;

	//1.初始化第0列
	for ( i = 0; i <=n; i++)
	{
		V[i][0] = 0;
	}

	//2.初始化第0行
	for ( j = 0; j <=C; j++)
	{
		V[0][j] = 0;
	}

	//3.初始化第i行，进行i次迭代
	for (i = 1; i <=n; i++)
	{
		for ( j = 1; j <= C; j++)
		{
			if (j<w[i-1])
			{
				//第j个物品重量大加不进去
				V[i][j] = V[i - 1][j];
			}
			else
			{
				V[i][j] = max(V[i - 1][j], V[i-1][j-w[i-1]]+v[i-1]);
			}
		}
	}

	//4.求装入的物品
	for ( j = C,i=n; i>0; i--)
	{
		if (V[i][j]>V[i-1][j])
		{
			x[i-1] = 1;
			j = j - w[i-1];
		}
		else
		{
			x[i-1] = 0;
		}
	}

	//5.返回背包的最大价值
	return V[n][C];
}

    • 回溯算法（dfs）

      void dfs(int i)
{
	if(i > n){
		if(valueofPackage >= maxTotalValue){
			for(int i = 1 ; i <= n ; i++){
				optimal[i] = selected[i];
			}
			maxTotalValue = valueofPackage;
		}
		return;
	}else{
		residualCapacity -= weight[i];
		if(residualCapacity >= 0){	//遍历左子树
			selected[i] = 1;
			valueofPackage += value[i];
			dfs(i+1);
			selected[i] = 0;
			valueofPackage -= value[i];
			residualCapacity += weight[i];
		}else{//不满足原路返回
			residualCapacity += weight[i];
		}
	}
	//遍历右子树
	dfs(i+1);
}

  6. 总结

    ​ 任务3是D{0-1}KP，D{0-1}KP是经典{0-1}背包问题的一个拓展形式，用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解，达到获利最大化。在解决此问题的过程中，我未能正确读入实验数据文件的有效D{0-1}KP数据，导致此次实验的失败。但是，我在此次实验的过程中，将PSP流程用到解决0-1背包问题的时候，体会到了软件设计的“模块化”原则。具体体现如下说明：

    • 运用两种不同的算法：动态规划算法和回溯算法解决0-1背包问题
    • 首先进行项目的需求分析，清晰的了解项目的需求
    • 其次对项目进行功能设计，了解项目需要满足的基本功能
    • 再次对项目进行设计实现，此时代码部分会有明显的类，需要明确这些类的功能以及它们之间的关系
    • 然后对项目进行测试运行，此时需要测试各种不同类型的数据以验证程序的正确性
    • 最后对工程项目进行反思总结，思考今后遇到此类问题时自己能够如何简化解决方法

  7. PSP展示

    PSP2.1
    任务内容
    计划共完成需要的时间（min）
    实际完成需要的时间（min）
    Planning 计划
    15
    13
    Estimate
    		 估计这个任务需要多少时间，并规划大致工作步骤
    15
    13
    Development 开发
    235
    277
    Analysis
    		 需求分析（包括学习新技术）
    50
    60
    Design Spec
    		 生成设计文档
    25
    30
    Design Review
    		 设计复审（和同事审核设计文档）
    10
    15
    Coding Standard
    		 代码规范（为目前的开发制定合适的规范）
    10
    10
    Design
    		 具体设计
    30
    35
    Coding
    		 具体编码
    60
    70
    Code Review
    		 代码复审
    20
    22
    Test
    		 测试（自我测试，修改代码，提交修改）
    30
    35
    Reporting 报告
    40
    34
    Test Report
    		 测试报告
    15
    12
    Size Measurement
    		 计算工作量
    10
    12
    Postmortem & Process Improvement Plan
    		 事后总结，并提出过程改进计划
    15
    10

    反思：

    • 通过任务1点评同学们的博客，我认识到了自己的不足之处，同学们的博客对我而言有很大的指导作用，在今后的学习中，我希望自己能够取长补短，书写博客时能够在内容和排版上更进一步；
    • 通过任务2阅读《构建之法》前2章，我对于PSP流程有了一定的认识。PSP流程对于我们今后开发软件项目有很大的指导作用，使过程更加清晰，结果的可预见性增强；
    • 通过任务3个人软件项目D{0-1}KP开发，我认识到自己在编程这一方面的严重不足，虽然自己对于0-1背包问题已经熟练掌握，但是只要问题一变形，自己就陷入进退两难的处境，导致此次作业对于任务3未能解决。我将在今后《软件工程》的学习中，加深自己对于《软件工程》的认识，努力提高自己的编程能力。“编程不牢，地动山摇”将是我今后学习的动力。
    • 通过任务4将项目源码的完整工程文件提交到Github账号的项目仓库中，我再次学习了对于Github的使用，体会到这个源代码管理工具的优势。

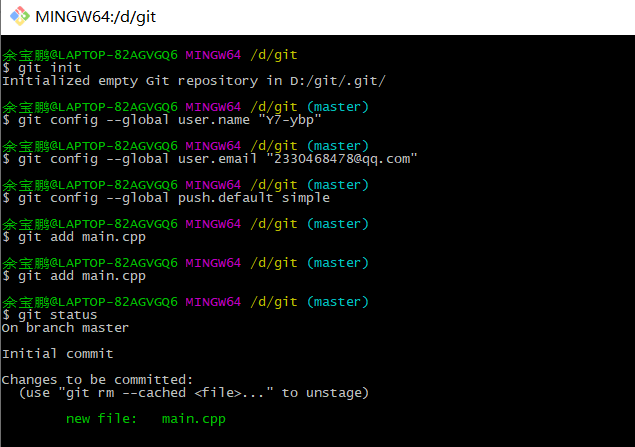
      • 在提交项目源码的完整工程文件的时候我查找了资料，配置了Git（参考这篇博客），然后使用了命令行方式进行了一些尝试操作，最后失败了，但还是了解到了很多git bush的命令，希望在今后的学习过程中查缺补漏，更进一步。

        1. git下载配置及文件夹创建

        2. git bush命令行操作

posted @ 2021-03-31 07:59  201871030134-余宝鹏  阅读(112)  评论(1)  编辑  收藏  举报