HDU 2571 命运
命运
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 8488 Accepted Submission(s):
2991
Problem Description
穿过幽谷意味着离大魔王lemon已经无限接近了!
可谁能想到,yifenfei在斩杀了一些虾兵蟹将后,却再次面临命运大迷宫的考验,这是魔王lemon设下的又一个机关。要知道,不论何人,若在迷宫中被困1小时以上,则必死无疑!
可怜的yifenfei为了去救MM,义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧!
命运大迷宫可以看成是一个两维的方格阵列,如下图所示:
![]()
yifenfei一开始在左上角,目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒,所以每个格子都对应一个值,走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走,向下一次只能走一格。但是如果向右走,则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子,即:如果当前格子是(x,y),下一步可以是(x+1,y),(x,y+1)或者(x,y*k) 其中k>1。
为了能够最大把握的消灭魔王lemon,yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。
![]()
可谁能想到,yifenfei在斩杀了一些虾兵蟹将后,却再次面临命运大迷宫的考验,这是魔王lemon设下的又一个机关。要知道,不论何人,若在迷宫中被困1小时以上,则必死无疑!
可怜的yifenfei为了去救MM,义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧!
命运大迷宫可以看成是一个两维的方格阵列,如下图所示:
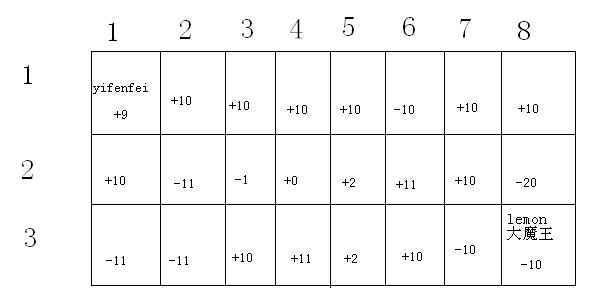
yifenfei一开始在左上角,目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒,所以每个格子都对应一个值,走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走,向下一次只能走一格。但是如果向右走,则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子,即:如果当前格子是(x,y),下一步可以是(x+1,y),(x,y+1)或者(x,y*k) 其中k>1。
为了能够最大把握的消灭魔王lemon,yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

Input
输入数据首先是一个整数C,表示测试数据的组数。
每组测试数据的第一行是两个整数n,m,分别表示行数和列数(1<=n<=20,10<=m<=1000);
接着是n行数据,每行包含m个整数,表示n行m列的格子对应的幸运值K ( |k|<100 )。
每组测试数据的第一行是两个整数n,m,分别表示行数和列数(1<=n<=20,10<=m<=1000);
接着是n行数据,每行包含m个整数,表示n行m列的格子对应的幸运值K ( |k|<100 )。
Output
请对应每组测试数据输出一个整数,表示yifenfei可以得到的最大幸运值。
Sample Input
1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10
Sample Output
52
状态转移方程 dp[i][j] = max(dp[i-1][j],maxx)+K[i][j],maxx = max(maxx,dp[i][k]),k是j的因子或者是j-1。

1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 #define minn -1000 5 int n, m; 6 int dp[25][1005]; 7 int K[25][1005]; 8 int max(int a,int b) 9 { 10 return a>b?a:b; 11 } 12 void solve() 13 { 14 int i, j, k, maxx; 15 for(i=0; i<=n; i++) 16 dp[i][0] = minn; 17 for(j=0; j<=m; j++) 18 dp[0][j] = minn; 19 for(i=1; i<=n; i++) 20 { 21 for(j=1; j<=m; j++) 22 { 23 maxx = minn; 24 for(k=1; k<j; k++) 25 if(j%k==0 || j-k==1) 26 maxx = max(maxx,dp[i][k]); 27 if(i==1 && j==1) 28 dp[i][j] = K[i][j]; 29 else 30 dp[i][j] = K[i][j]+max(dp[i-1][j],maxx); 31 } 32 } 33 } 34 35 int main() 36 { 37 int C, i, j; 38 scanf("%d",&C); 39 while(C--) 40 { 41 scanf("%d%d",&n,&m); 42 for(i=1; i<=n; i++) 43 for(j=1; j<=m; j++) 44 scanf("%d",&K[i][j]); 45 solve(); 46 printf("%d\n",dp[n][m]); 47 } 48 return 0; 49 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号