Java 类型转换精度问题
基本数据类型占用内存大小
最近项目中修复了一个关于类型转换精度丢失的问题,以前对于类型转换会丢失精度只知其然,不知其所以然,这次了解了下相关原理,也分享给大家。先来回顾一下 Java 的基本数据类型中整型与浮点型及其所占用的内存大小:
整型:
- int:4 字节 32 位
- long:8 字节 64 位
浮点型:
- float:4 字节 32 位
- double:8 字节 64 位
Java 运算时,当两个不同类型的数进行基本运算符操作时,低精度会自动向高精度转换,字节短的会自动向字节长的转换。
《Java 核心技术》一书中这么归纳到:
如果两个操作数其中有一个是 double 类型,另一个操作就会转换为 double 类型。
否则,如果其中一个操作数是 float 类型,另一个将会转换为 float 类型。
否则,如果其中一个操作数是 long 类型,另一个会转换为 long 类型。
否则,两个操作数都转换为 int 类型。
需要注意 Java 自动转换类型可能会带来精度的丢失,附上一张不会丢失精度的合法类型转换说明图:
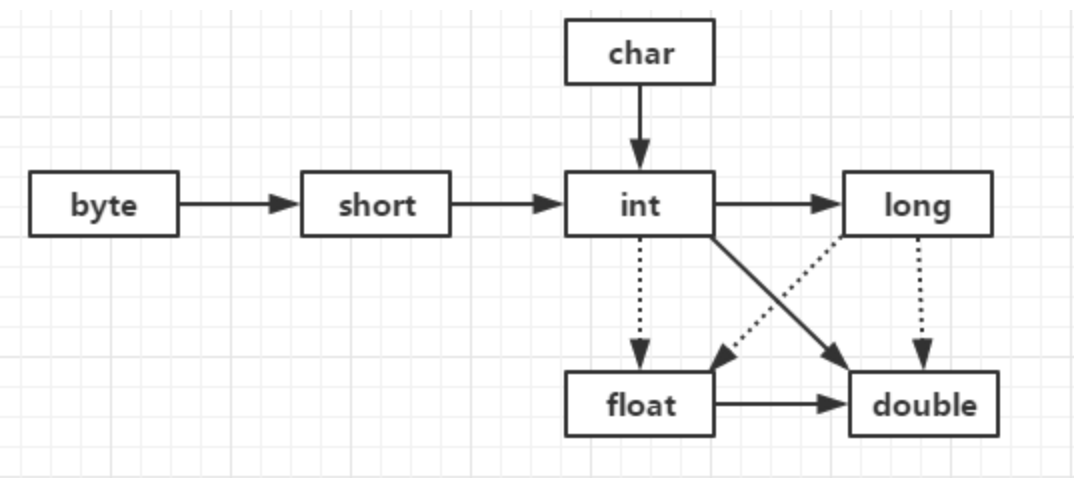
图中实现箭头类型转换代表不会丢失精度,虚线箭头类型转换可能会丢失精度。
基本数据类型表示范围
精度和数据类型可表示的数值大小范围息息相关,计算机中所有数值归根到底都是使用二进制 0、1 来组成,因此一个数据类型所占用的内存大小越大,就意味着可用的二进制位数越多,当然可表示的范围就越大。回顾一下几个常见的参与运算的基本数据类型的取值范围:
int
二进制位数:32
最小值:Integer.MIN_VALUE= -2147483648 (-2 的 31 次方)
最大值:Integer.MAX_VALUE= 2147483647 (2 的 31 次方 -1)
long
二进制位数:64
最小值:Long.MIN_VALUE=-9223372036854775808 (-2 的 63 次方)
最大值:Long.MAX_VALUE=9223372036854775807 (2 的 63 次方 -1)
float
二进制位数:32
最小值:Float.MIN_VALUE=1.4E-45 (2 的 -149 次方)
最大值:Float.MAX_VALUE=3.4028235E38 (2 的 128 次方 -1)
double
二进制位数:64
最小值:Double.MIN_VALUE=4.9E-324 (2 的 -1074 次方)
最大值:Double.MAX_VALUE=1.7976931348623157E308 (2 的 1024 次方 -1)
当 long 类型的数大于 Integer.MAX_VALUE 时,long 强制转换 int,就会出现丢失精度。转换过程是将 long 类型数值的二进制数从低位到高位截取 32 位,再将 32 位二进制数转为 int。
long l3 = 24696061952L; //10111000000000000000000000000000000
int c3 = (int)l3; //-1073741824
System.out.println(Integer.toBinaryString(c3)); //1000000000000000000000000000000
上面的例子中,long 类型截取 32 位后转为 int,最高位作为符号位,1 代表负数,强转后的 int 值为 -1073741824。
类似这种不合理的强制转换丢失的已经不仅仅是精度了。
不知道有没有人注意到,long 类型的二进制位数是 64,float 类型的二进制位数是 32,但是 float 类型可表示范围却远远大于 long 类型。更不用提一样是 32 位的 int 了,float 到底啥家庭啊?谜底就在内存结构中。
浮点类型数值的内存结构
与整形类型的内存结构不同,float 在内存中是这样的:
SEEE EEEE EMMM MMMM MMMM MMMM MMMM MMMM
- S:最高位 S 代表符号位
- E:后面 8 位 E 代表指数域,二进制中就是 2 的 n 次方,采用移位存储(127+指数)的二进制方式。
- M:剩下的 23 位 M 代表小数域。规定小数点前的数必须为 1,因此只记录小数点后的数。(从左往右,低位补零)
以 7.8125 为例,整数十进制转二进制,除 2 取余,逆序排列,求得 7 二进制为 111。小数十进制转二进制,乘 2 取整,顺序排列,求得 0.8125 二进制为:0.1101,组合起来是 111.1101。
根据规范,小数点前的数只保留 1,因此将 111.1101 小数点左移两位得 1.111101 * 2^2。
符号位 0,指数位为 2+127=129,即二进制 10000001,小数域为 111101。因此 float 数 7.8125 在内存中存储的格式为:0 10000001 111101 低位补零补齐到 32 位,得:0100 0000 1111 1010 0000 0000 0000 0000。
可以使用 Java 提供的 API 验证一下:
int i = Float.floatToIntBits(7.8125F); //得到 7.8125F 底层数据(十进制)
Integer.toBinaryString(i); //得到指定 int 值的二进制数
//输出 1000000111110100000000000000000
//补上最高位符号位 0,结果与上面计算的一样。
通过对浮点类型数值内存结构的了解,我们知道了 float 虽然可用于存储数值的位数没有 long 型多,但是 float 通过使用指数进行降维打击,可表示范围蹭蹭蹭往上涨。
double 的内存结构同理,只不过 double 二进制位数更多,总共 64 位分别分配给:符号位 1 位,指数位 11 位,小数位 52 位。
需要注意的是,虽然 float 因为有指数的概念,可表示范围变大了,但是其用于存储小数的位数却只有 23 位。这就意味着当一个整型类型数值的二进制位大于 24 位时,类型转换到 float 就会带来精度丢失了。
整型转换浮点型的精度丢失问题
看到上图中的int 转 float、long 转 float 都是虚线表示,代表运算时自动类型转换可能会出现精度丢失的问题。经过上面对浮点型数据内存结构的学习,我们应该不难理解,float 能表示的数的大小靠指数位,但是表示的数的精度需要靠小数位。而 float 的小数位只有 23 位,而 int 是 32 位。
举个例子:int 值 16777217,二进制数 1 0000 0000 0000 0000 0000 0001,除去最高位符号位后,需要 25 位表示。
顺带提一下,计算某个数值除了符号位外需要多少位二进制位可以表示,除了挨个去数二进制数外,还可以直接计算 log2 的值:
int i = 16777217;
double num = Math.log(i) / Math.log(2.0);
//num = 24.000000085991324,即需要 25 位二进制位表示
int 转 float,转换过程是先将 int 的数值由十进制转为二进制,再通过对二进制数左移小数点直到个位为 1,变为:1. 0000 0000 0000 0000 0000 0001 * 2 ^ 24,转换后的数小数点后有 24 位,对 float 来说只能舍弃掉无法表示的位数,只保留 23 位小数位,指数位 24 + 127 = 151,二进制为 10010111,因此转换后的 float 二进制数为 110010111 + 23个0,float 值为 1.6777216E7,已经丢失了精度。
同理,int 转 double,由于 double 有 52 位小数位,因此足以 hold 住 int 的精度,而 long 需要 64 位表示精度,因此 long 转 double 也可能出现精度丢失。另外需要注意的是,单位秒的时间戳,也需要 31 位来表示,用 int 表示是够的,但是转 float 也一样会丢失精度。
以上就是对 Java 类型转换精度问题的分析,希望对你有帮助 😛



 浙公网安备 33010602011771号
浙公网安备 33010602011771号