数据库系统概论(一)关系数据理论--数据依赖的公理系统和模式分解
Armstrong公理系统
对R(U,F)有:
1.自反律:若Y⊆X⊆U,则F蕴含X→Y
2.增广律:若X→Y,且 Z⊆U,则F蕴含XZ→YZ
3.传递律:若F蕴含X→Y,Y→Z,则有X→Z
由以上定律可以推出以下规则
1.合并规则:若X→Y,X→Z,则有X→YZ
2.伪传递规则:X→Y,WY→Z,则有WX→Z
3.分解规则:X→Y,Z⊆Y,则有X→Z
闭包
闭包F+:在关系模式R(U,F)中由F推导出的全部函数依赖称F+
X关于F的闭包XF+:由X能在F中推导出的所有函数依赖合集
若F=F+,则称F为完备集
判定X→Y能否由F推导出的问题,转化为求出XF+,判定Y是否为XF+子集
Armstrong公理系统的有效性与完备性
有效性:由F出发根据Armstrong公理系统推导出的每一个函数依赖都存在于F+中
完备性:F+中每一个函数依赖,必定可以由F出发根据Armstrong公理系统推导出
最小函数依赖集
如果函数依赖集F满足以下条件,则称F为一个极小函数依赖集。也称为最小依赖集或最小覆盖。
(1)F中任一函数依赖的右部仅含有一个属性。
(2)F中不存在这样的函数依赖X→A,使得F与F-{X→A}等价(任一函数依赖不能由其他函数依赖推导出,线性无关)
(3)F中不存在这样的函数依赖X→A,X有真子集Z使得(F-{X→A}) U {Z→A}与F等价。(F中各函数依赖左边都是最小属性集,无冗余属性)
最小依赖集并不唯一
求最小依赖集
① 用分解的法则,使F中的任何一个函数依赖的右部仅含有一个属性;
② 去掉多余的函数依赖:从第一个函数依赖X→Y开始将其从F中去掉,然后在剩下的函数依赖中求X的闭包X+,看X+是否包含Y,若是,则去掉X→Y;否则不能去掉,依次做下去。直到找不到冗余的函数依赖;
③ 去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖。例如XY→A,若要判Y为多余的,则以X→A代替XY→A是否等价?若A属于(X)+,则Y是多余属性,可以去掉。(以上步骤中,求出关系依赖集F,此时,再F的基础上,求出X或者Y的闭包,是否包含A)
例1:关系模式R(U,F)中,U=ABCDEG,F={B->D,DG->C,BD->E,AG->B,ADG->BC};求F的最小函数依赖集
步骤:
(1)用分解的法则,使F中的任何一个函数依赖的右部仅含有一个属性;得到:F={B->D,DG->C,BD->E,AG->B,ADG->B,ADG->C};
(2)去掉多余的函数依赖:从第一个函数依赖X→Y开始将其从F中去掉,然后在剩下的函数依赖中求X的闭包X+,依次做下去。直到找不到冗余的函数依赖;
① 去掉B->D,此时F={DG->C,BD->E,AG->B,ADG->B,ADG->C},此条件下得出B的闭包 B+ = B;B+不包含D,所以B->D保留。
②去掉DG->C,此时F={B->D,BD->E,AG->B,ADG->B,ADG->C},此时DG闭包DG+ = DG,不包含C,所以不能去掉DG->C.
③ 去掉BD->E,此时F={B->D,DG->C,AG->B,ADG->B,ADG->C},此时闭包BD+ = BD,不包含E,所以不能去掉BD->E,继续保留。
④去掉AG->B,此时F={B->D,DG->C,BD->E,ADG->B,ADG->C};此时AG+ = AG,不包含B,所以不能去掉AG->B,继续保留。
⑤去掉ADG->B,此时F={B->D,DG->C,BD->E,AG->B,ADG->C},此时ADG+ = ADGCBE,包含了B,所以删除ADG->B,不保留。
⑥去掉ADG->C,此时F={B->D,DG->C,BD->E,AG->B},此时ADG+ = ADGCBD,包含了C,所以删除ADG->C,不保留。
综上所得,此时得到F={B->D,DG->C,BD->E,AG->B};
(3)去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖。
此时函数依赖左边非单个属性有:DG->C,BD->E,AG->B;所以做如下操作:
①先来看DG->C,首先去掉D,则此时G的闭包G+ = G,不包含C,保留D。再次去掉G,此时D+ = D,不包含C,所以G也不能去掉;
②再来看BD->E,首先去掉B,得到此时D的闭包D+ = D,不含E,保留B。然后去掉D,此时B+ = BDE,包含了E,所以去掉D,即得出:B->E;
③最后再来看AG->B,去掉A,G+ = G,不包含B,不能去掉A。去掉G的时候,A的闭包A+ =A,不含B,不能去掉A,还是AG->B ;
所以最后得出:F的最小函数依赖集是:F={B->D,DG->C,B->E,AG->B};
模式分解
要保证分解后的模式与原模式等价,则要满足以下两个性质
无损连接性:数据内容的等价
保持函数依赖性:数据约束的等价
1.无损连接分解的检测方法(判断一个分解是否无损连接):
方法一:
算法:

(1)案例:
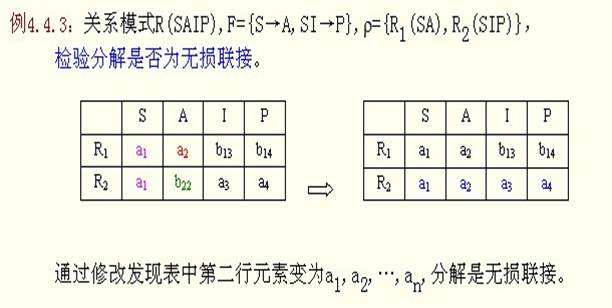
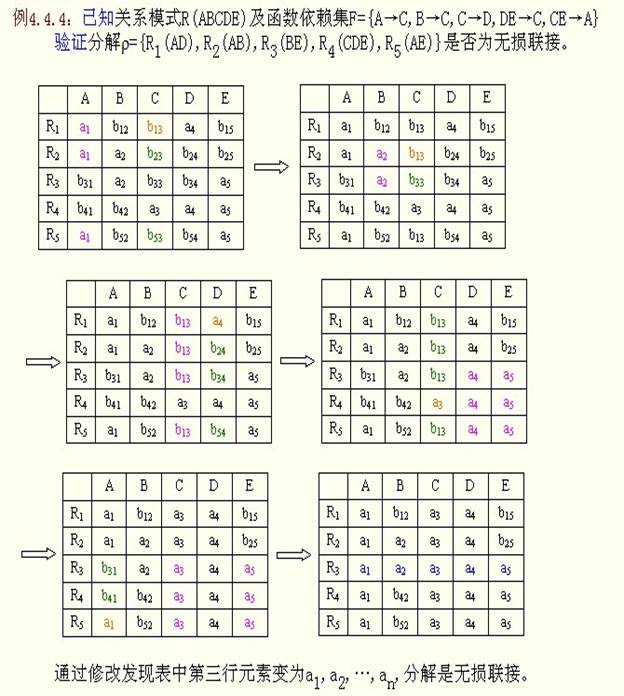
方法二:无损连接定理(更易于使用):

案例(1):
关系模式R(SAIP),F={S—>A,SI—>P}; ρ={R1(SA),R2(SIP)}检测分解是否为无损连接?
因为:R1∩R2 = S ;R1—R2 = A; R2—R1 = IP;所以得出:S —>A;或者S —>IP; 而 S —>A 在F={S—>A,SI—>P}中,所以此分解是无损连接。
举例(2):已知R<U,F>,U={A,B,C},F={A→B},如下的两个分解:
① ρ1={AB,BC};
② ρ2={AB,AC};
因为:AB∩BC = B;AB—BC = A;BC—AB = C;得出;B→A,或者 B→A,两个都不包含在F={A→B}中,所以 ρ1 分解是有损的。
因为:AB∩AC = A;AB—AC = B;AC—AB = C;得出:A→B,或者A→C,而A→B包含在F={A→B}中,所以 ρ2 分解是无损的。
2.保持依赖分解的检测方法(判断一个分解是否保持依赖):
算法:
如果F上的每一个函数依赖都在其分解后的某一个关系上成立,则这个分解是保持依赖的(这是一个充分条件)。
如果上述判断失败,并不能断言分解不是保持依赖的,还要使用下面的通用方法来做进一步判断。
该方法的表述如下:
算法二:
对F上的每一个α→β使用下面的过程:
result:=α;
while(result发生变化)do
for each 分解后的Ri //将每个分解后的结构Ri逐个带入
t=(result∩Ri)+ ∩Ri //这里的意思是取result与Ri的交集的闭包值,之后再与Ri取交集
result=result∪t
这里的属性闭包是在函数依赖集F下计算出来的。如果result中包含了β的所有属性,则函数依赖α→β。分解是保持依赖的当且仅当上述过程中F的所有依赖都被保持。
案例(1):
关系模式R<U, F>,U={A, B, C, D, E},F={B→A,D→A,A→E,AC→B}则分解ρ={R1(ABCE),R2(CD)}是否满足保持函数依赖。
因为:B→A,A→E,AC→B在R1上成立,D→A在R1和R2上都不成立,因此需做进一步判断。
由于B→A,A→E,AC→B都是被保持的(因为它们的元素都在R1中),因此我们要进一步判断的是D→A是不是也被保持。
①先看R1:因为:result = D;result ∩R1 = ф (空集);所以:t=ф,result=D;
②再看R2:因为:result = D;result ∩R2 = D;D+ = DA; D+ ∩ R2 = D; 所以:t=D,result=D;
一个循环后result未发生变化,因此最后result=D,并未包含A,所以D→A未被保持,该分解不是保持依赖的。
案例(2):
关系R<U,F>,U={A,B,C,D,E},F={A→C,B→C,C→D,DE→C,CE→A},R的一个分解为R1(AD),R2(AB),R3(BE),R4(CDE),R5(AE),判断这个分解是否具有函数依赖性。
因为:,C→D,DE→C均在R4(CDE)中被保持,而A→C,B→C,CE→A,在R1....R5上都不成立,需要进一步判断。
(1)A→C;
①先看R1:因为:result = A;result ∩R1 = A ; A+ = ACD ; A+ ∩ R1 = AD;所以:t=AD,result=AD; 此时,result改变,则,进入R2;
②再看R2:因为:result = AD;result ∩R2 = ф,最后还是result = AD;
③再看R3:因为:result = AD;result ∩R3 = ф,最后还是result = AD;
④再看R4:因为:result = AD;result ∩R4 = D,D+ = D; D+ ∩ R4= D;最后还是result = AD;
⑤再看R5:因为:result = AD;result ∩R5 = A,最后还是result = AD;
最后result = AD 并未包含C;所以,所以D→A未被保持,该分解不是保持依赖的;
综合案例:
设有关系模式R<U,F>,U={A,B,C,D,E},F={A→D,E→D,D→B,BC→D,CD→AB},设有一个分解P={R1(ED),R2(BCD),R3(ACD)}判断该分解是否保持函数依赖,并判断此分解是否具有无损连接性。
①判断是保持函数依赖的;F的最小函数依赖为:F={A→D,E→D,D→B,BC→D,CD→A};三个分解的模式中满足依赖的传递。
②判断是有损的模式分解; (没有一行全为a的);

3.关系模式保持依赖地分解成3NF:

分解规则:将每一个函数依赖单独组成一个关系;
案例(1):
关系R<U,F>,U={A, B, C, D, E, F, G},F={A→B,A→C,C→D,C→E,E→FG},将R分解成3NF。(有非主属性传递依赖于码,不属于3NF目前);
①:U中所有元素均存在F中,进一步判断; F中并不存在依赖函数X→A,且XA = R;
②:将每一个函数依赖组成一个关系;即:ρ = {R1(A,B),R2(A,C),R3(C,D),R4(C,E),R5(E,F,G)};
③:合并关系(跟进F左边相同):即:ρ = {R1(A,B,C),R2(C,D,E),R3(E,F,G)};
案例(2):关系模式R<U,F>,其中U={C,T,H,R,S,G},F={CS→G,C→T,TH→R,HR→C,HS→R},将其分解成3NF并保持函数依赖。
因为:最小依赖集为:F={CS→G,C→T,TH→R,HR→C,HS→R}; 而U中所有元素 均在 F中有出现;
所以:可将每一个函数依赖单独组成一个关系;即:ρ = {R1(CSG),R2(CT),R3(THR),R4(HRC),R5(HSR)};
4.关系模式无损连接地分解成BCNF:

分解规则:将左侧不含候选键的函数依赖单独组成一个关系, 将包含候选键的组成一关系;
案例(1):
关系R<U,F>,U={A, B, C, D, E, F, G},F={A→B,A→C,C→D,C→E,E→FG},将R分解成BCNF;(目前,有 不依赖于 候选键的其他函数依赖,不满足BCNF);
①找出候选码:A;
②将左侧不含候选码的组成一个关系,包含候选码的组成一个关系:ρ = {R1(C,D),R2(C,E),R3(E,F,G),R4(A,B,C)};
③合并关系:即:ρ = {R12(C,D,E),R3(E,F,G),R4(A,B,C)};
案例(2):
关系模式R<U,F>,其中U={C,T,H,R,S,G},F={CS→G,C→T,TH→R,HR→C,HS→R},将其分解成BCNF并保持无损连接。
①找出候选码:HS;
②将左侧不含候选码的组成一个关系,包含候选码的组成一个关系:ρ = {R1(C,T),R2(S,G,C,R,G)};(即:R2中不能含T);
计算此时R1和R2的最小函数依赖集分别为:F1={C→T},F2={CS→G,CH→R,HR→C,HS→R}(因为R2中不能含有T,根据C→T,TH→R,可以转化成CH→R);
又因为:R1(C,T)、F1={C→T}(已满足BCNF);
R2(S,G,C,R,G)、F2={CS→G,CH→R,HR→C,HS→R};此时R2的码为:HS;而F中箭头左侧有不是如CS、CH、HR不是码,故不满足BCNF,需要进一步分解;
分解R2: R2(S,G,C,R,G)、F2={CS→G,CH→R,HR→C,HS→R};得:R21(CSG),R22(CHR),R23(HSR);(左侧不含候选码的组成一个关系); 此时:R21、R22、R23均已满足BCNF;
③最终分解后得出:ρ = {R1(C,T),R21(CSG),R22(CHR),R23(HSR)};
案例(3):
关系模式R<U,F>,其中:U={A,B,C,D,E},F={A→C,C→D,B→C,DE→C,CE→A},将其分解成BCNF并保持无损连接。
①找出候选码:BE;
②因为目前左侧都不包含码。不能组成一个包含码的关系。
考虑A→C函数依赖不满足BCNF条件(因A不包含候选键BE),将其分解成R1(AC)、R2(ABDE)。 (R2中不能包含C);
计算此时R1和R2的最小函数依赖集分别为:F1 = {A→C};F2 = {B→D,BE→A};(因为C→D,B→C,DE→C,CE→A,R2中不能包含C,而C→D,B→C,可以转化成:B→D;DE→C 可以转化成 DE→D,CE→A 可以转化成BE→A);又由于DE→D是蕴含关系,可以去掉;
③分解R2:R2上的候选关键字为BE。考虑B→D函数依赖不满足BCNF条件,将其分解成R21(BD)、R22(ABE)。计算R21和R22的最小函数依赖集分别为:F21={B→D},F22={BE→A}。
由于R22上的候选关键字为BE,而F22中的所有函数依赖满足BCNF条件。故R可以分解为无损连接性的BCNF如:ρ={R1(AC),R21(BD),R22(ABE)}。
5.关系模式分解既保持依赖又无损连接:
分解规则:将R的一个保持依赖的分解,再并上候选码; 即:(原模式)候选码 U 保持依赖的3NF分解;
案例(1):关系模式R<U,F>,其中:U={C,T,H,R,S,G},F={CS→G,C→T,TH→R,HR→C,HS→R},分解成3NF并保持无损连接和函数依赖。
①找出候选码: HS;
②模式分解成保持依赖的3NF为:ρ={R1(GSC),R2(CT),R3(THR),R4(HRC),R5(HSR)};
③将原候选码,作为一个关系,加入ρ中,即:τ={CT,CSG,CHR,HSR,HRT,HS};
而由于:HS是模式HSR的一个子集,所以消去HS后的分解{CT,CSG,CHR,HSR,HRT}就是具有无损联接性和保持函数依赖性的分解,且其中每一个模式均为3NF。
案例(2):已知:关系模式R(U,F) U=ABCD F={A→C,C→A,B→AC,D→AC},将模式R无损失连接且保持函数依赖分解为3NF。
①找出候选码: BD;
②求出关系F的最小依赖集:F={A→C,C→A,B→C,D→C};
③模式分解成保持依赖的3NF为:ρ={R1(AC),R2(BC),R3(CD)};
④将模式R无损失连接且保持函数依赖分解为3NF:ρ={R1(AC),R2(BC),R3(CD),R4(BD)};
————————————————
版权声明:本文为CSDN博主「prdslf001001」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/prdslf001001/article/details/80336835



