线性代数 -- Linear Algebra with Applications
@、如果线性方程组无解,则称该方程组是不相容的(inconsistent)。
@、如果线性方程组至少存在一个解,则称该方程组是相容的(consistent)。
@、等价方程组(equivalent systems)。
@、定义:若两个含有相同变量的方程组具有相同的解集,则称它们是等价的(equivalent)。
@、得到等价的方程组:
1、交换任意两个方程的顺序。
2、任一方程两边同乘一个非零的实数。
3、任一方程的倍数加到另一方程上。
@、定义:若方程组中,第k个方程的前k-1个变量的系数均为零,且xk(k=1, ..., n)的系数不为零,则称该方程组为严格三角形的(strict triangular form)。
@、求解严格三角形方程组的方法:回代(back substitution)。
@、方程组的系数矩阵(coefficient matrix)。
@、方程组的增广矩阵(augmented matrix)。
@、初等行运算:
1、交换两个。
2、以非零实数乘以某行。
3、将某行替换为它与其他行的倍数的和。
@、主行(pivotal row):用来消去其他行元素。
@、主元(pivot):主行的第一个非零元素。
@、首变量(lead variables):化简后增广矩阵每一行第一个非零元对应的变量。
@、自由变量(free variables):化简过程中跳过的列对应的变量(即除了首变量的变量)。
@、定义:若一个矩阵满足
1、每一非零行中的第一个非零元为1;
2、第k行的元不全为零时,第k+1行首变量之前的零的个数多于第k行首变量之前零的个数;
3、所有元素均为零的行必在不全为零的行之后。
则称为行阶梯形矩阵(row echelon form)。
@、高斯消元法(Gaussian elimination):定义: 利用行运算1、2和3,将线性方程组的增广矩阵化为行阶梯形的过程称为高斯消元法。
@、超定方程组:若一个线性方程组中方程的个数多于未知量的个数,则称其为超定的(overdetermined)。超定方程组通常是(但不总是)不相容的。
@、亚定方程组:若一个线性方程组中方程的个数(n)多于未知量的个数(m),则称其为亚定的(underdetermined)。亚定方程组有可能不相容,但通常是相容的,其有无穷多个解。因为行阶梯形式均有r(r<=m)个首变量,那么必有n-r(n-r>=n-m>0)个自由变量,当自由变量取不同值时,可得到不同的解。
@、定义 若一个矩阵满足
1、 矩阵是行阶梯形的;
2、每一行的第一个非零元是该列惟一的非零元,
则称该矩阵为行最简形(reduced row echelon form)。
@、高斯 - 若尔当消元法(Gauss-Jordan reduction):采用基本行运算将矩阵化为行最简形的过程。
@、齐次方程组:如果线性方程组的右端项全为零,则称其为齐次的(homogeneous)。齐次方程组总是相容的,至少有一个平凡解。
@、平凡解:(0, 0, ..., 0)。即所有变量的值都为零。
@、非平凡解:不是(0, 0, ..., 0)的解。
@、定理1.2.1 若n>m,则m * n的齐次线性方程组有非平凡解。

@、矩阵中的元素称为标量(scalar)。通常是实数或复数。
@、一般若用A表示矩阵,则aij表示矩阵A的第i行第j列的元素。矩阵简记为:A = (aij)。
@、向量(vector):由实数组成的n元组。
@、行向量(row vector):用一个1*n的矩阵来表示n元组。
@、列向量(column vector):用一个n*1的矩阵来表示n元组。
@、在使用矩阵方程时,用列向量表示解较为方便,所以n*1的实矩阵构成的几何称为n维欧几里得空间(Euclidean n-space),通常记为Rn。
@、定义 若两个m*n矩阵A和B对任一i和j均满足aij = bij,则称它们相等(equal)。
@、标量乘法:定义:设A为m*n的矩阵,且α为一标量,则αA为一m*n的矩阵,其(i, j)元素为αaij。
@、矩阵加法:定义:设A=(aij)及B=(bij)都是m*n矩阵,则它们的和(sum)A+B也为一个m*n的矩阵,对每一个有序对(i, j),它的(i, j)元素为aij + bij。
@、零矩阵(zero matirx):元素全为零的矩阵。用O表示。
@、A与O都是m*n的矩阵,O是零矩阵,则:
1、A + O = O + A = A;
2、A + (-1)A = O = (-1)A + A;
@、定义 若a1, a2, ..., an 为Rm中的向量,且c1, c2, ..., cn为标量,则和式 c1a1 + c2a2 + ... + cnan 称为向量 a1, a2, ..., an 的一个线性组合(linear combination)。
@、定理1.3.1(线性方程组的相容性定理) 一个线性方程组 Ax = b 相容的充要条件是向量 b 可写为矩阵 A 列向量的一个线性组合。
@、定义 若 A=(aij)为一个 m*n 的矩阵,且B=(bij)为一个 n*r 的矩阵,则乘积AB=C=(cij)为一个 m*r 的矩阵,它的元素定义为:cij = a→ibj = ∑aikbkj 。(注:a→i表示矩阵A的第i个行向量)
@、矩阵乘法不满足交换率,即 AB != BA。
@、定义 一个 m*n 矩阵A的转置(transpose)为 n*m 矩阵B,定义为 bji = aij 其中j=1, ..., n 和 i=1, ..., m. A的转置记为AT。
@、定义 一个 n*n 的矩阵A, 若满足AT=A,则称为对称的(symmetric)。
@、矩阵代数的法则:

@、单位矩阵(identity matrix): I = (δij),其中δij = 1(当 i = j)或者 0 (当 i ≠ j)。 BI = B, IC = C。
@、使用列向量表示I, I = (e1, e2, ..., en),不使用 ij。
@、定义 若存在一个矩阵B使得AB=BA=I,则称 n*n 矩阵A为非奇异的(nonsingular)或可逆的(invertible)。矩阵B称为A的乘法逆元(multiplication inverse)。
@、若B和C均为A的乘法逆元,则 B = BI = B(AC) = (BA)C = IC = C,因此,一个矩阵最多有一个乘法逆元。A的逆元记作A-1。
@、定义 一个 n*n 矩阵若不存在乘法逆元,则称为奇异的(singular)。
@、只有方阵(即矩阵行数等于列数)有乘法逆元。对于非方阵,不应使用术语奇异或非奇异。
@、定理1.4.2 若A和B为非奇异的n*n矩阵,则AB也为非奇异的,且(AB)-1 = B-1A-1。

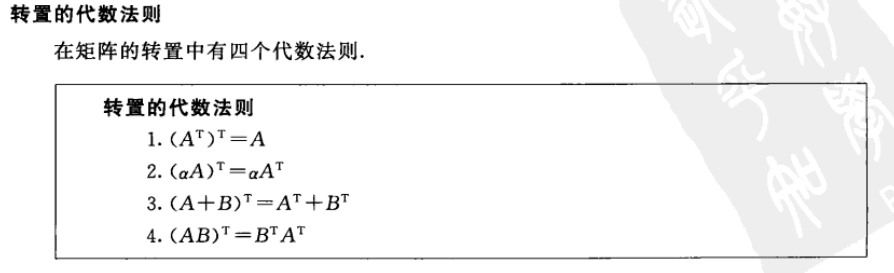
@、转置的代数法则:
@、定理1.4.3 设A为某图的n*n邻接矩阵,且a(k)ij表示Ak的(i, j)元素,则a(k)ji等于顶点Vi和Vj间长度为k的路的条数。

