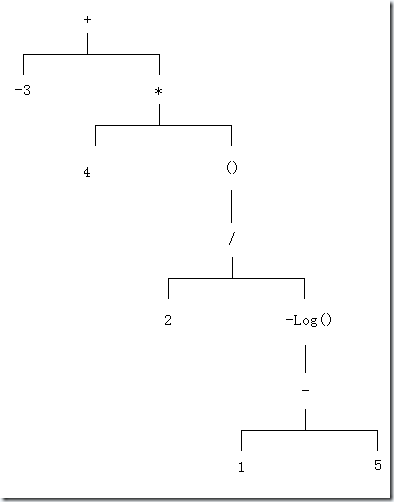
问题:实现一个解析器,可以将文本解析成表达式树;例如:"-3 + 4 * (2 / -log( 1 - 5 ))"
表达式数据结构:操作符 + – × / (),常数,等等,都应被定义为一种类。特别说明,将括号定义为一种表达式是很有必要的。对于负号的处理,可以在表达式类中加入一个成员变量做标记;
解析器:上面的树状结构是结果,获得这个树,就需要对字符进行解析,来创建树,基本逻辑如下。
1,从左到右读字符串,如果是空格,忽略;如果是常数,创建一个常数表达式;如果是括号,将括号里的字符串提取出来,递归,括号里的字符串会被解析为一个表达式;如果是函数,将函数括号里的字符串提取出来,递归,得到一个表达式作为函数表达式的操作数;如果是操作符,提取操作符,按字符串保存;最终结果,得到一个表达式对象和字符串的混合数组;
2,处理负号,将负号并入表达式里;
3,按操作符操作优先级建立操作符表达式;
代码:示例代码,不完整。
表达式类
using System; using System.Collections.Generic; using System.Linq; using System.Numerics; using System.Text; namespace Program { public enum EquResultDataType { rtConst, rtComplexArry } public class EquationException : Exception { public EquationException(string msg) : base(msg) { } public EquationException(string msg, Exception innerExp) : base(msg, innerExp) { } } public abstract class Equation { virtual public object Evaluate() { throw new NotImplementedException(); } public EquResultDataType ResultDataType { get; protected set; } // if the equation start with a ' - ' private double _sign = 1.0; protected double Sign { get { return _sign; } } virtual public void MultiplyMinusOne() { _sign *= -1.0; } virtual public string ToEquationText() { throw new NotImplementedException(); } } public class BinaryEquation : Equation { public Equation LeftOperand { get; set; } public Equation RightOperand { get; set; } } public class UnaryEquaton : Equation { public Equation Operand { get; set; } } public class EquAddition : BinaryEquation { public override object Evaluate() { object leftResult = LeftOperand.Evaluate(); object rightResult = RightOperand.Evaluate(); if (LeftOperand.ResultDataType == EquResultDataType.rtComplexArry && RightOperand.ResultDataType == EquResultDataType.rtComplexArry) { Complex[] leftData = leftResult as Complex[]; Complex[] rightData = rightResult as Complex[]; if (leftData.Length != rightData.Length) throw new EquationException(string.Format("{0}, {1}: data length are not equal.", LeftOperand.ToEquationText(), RightOperand.ToEquationText())); else { Complex[] result = new Complex[leftData.Length]; for (int i = 0; i < leftData.Length; ++i) { result[i] = leftData[i] + rightData[i]; } if (Sign < 0) { for (int i = 0; i < result.Length; ++i) result[i] *= -1.0; } return result; } } else if (LeftOperand.ResultDataType == EquResultDataType.rtComplexArry && RightOperand.ResultDataType == EquResultDataType.rtConst) { Complex[] leftData = leftResult as Complex[]; double rightData = (double)rightResult; Complex[] result = new Complex[leftData.Length]; for (int i = 0; i < leftData.Length; ++i) { result[i] = leftData[i] + rightData; } if (Sign < 0) { for (int i = 0; i < result.Length; ++i) result[i] *= -1.0; } return result; } else if (LeftOperand.ResultDataType == EquResultDataType.rtConst && RightOperand.ResultDataType == EquResultDataType.rtComplexArry) { double leftData = (double)leftResult; Complex[] rightData = rightResult as Complex[]; Complex[] result = new Complex[rightData.Length]; for (int i = 0; i < rightData.Length; ++i) { result[i] = leftData + rightData[i]; } if (Sign < 0) { for (int i = 0; i < result.Length; ++i) result[i] *= -1.0; } return result; } else if (LeftOperand.ResultDataType == EquResultDataType.rtConst && RightOperand.ResultDataType == EquResultDataType.rtConst) { double leftData = (double)leftResult; double rightData = (double)rightResult; double result = leftData + rightData; if (Sign < 0) result *= -1.0; return result; } else { throw new EquationException("Child equation evaluate error!"); } } public override string ToEquationText() { return LeftOperand.ToEquationText() + " + " + RightOperand.ToEquationText(); } } public class EquSubtraction : BinaryEquation { public override object Evaluate() { throw new NotImplementedException(); } public override string ToEquationText() { return LeftOperand.ToEquationText() + " - " + RightOperand.ToEquationText(); } } public class EquMultiplication : BinaryEquation { public override object Evaluate() { throw new NotImplementedException(); } public override string ToEquationText() { return LeftOperand.ToEquationText() + " * " + RightOperand.ToEquationText(); } } public class EquDivision : BinaryEquation { public override object Evaluate() { throw new NotImplementedException(); } public override string ToEquationText() { return LeftOperand.ToEquationText() + " / " + RightOperand.ToEquationText(); } } public class EquParenthesis : UnaryEquaton { public override object Evaluate() { if (Sign < 0) Operand.MultiplyMinusOne(); object result = Operand.Evaluate(); return result; } public override string ToEquationText() { string txt = "( " + Operand.ToEquationText() + " )"; if (Sign < 0) txt = "-" + txt; return txt; } } public class EquConstant : UnaryEquaton { double _const = 0.0; public EquConstant(double c) { _const = c; } public override void MultiplyMinusOne() { _const *= -1.0; } public override object Evaluate() { return _const; } public override string ToEquationText() { return _const.ToString(); } } public class EquFunction : UnaryEquaton { public override object Evaluate() { object val = Operand.Evaluate(); switch (Operand.ResultDataType) { case EquResultDataType.rtConst: { double d = (double)val; ResultDataType = EquResultDataType.rtConst; double result = Math.Log(d); if (Sign < 0) result *= -1.0; return result; } case EquResultDataType.rtComplexArry: { Complex[] arr = val as Complex[]; for (int i = 0; i < arr.Length; ++i) arr[i] = Complex.Log(arr[i]); ResultDataType = EquResultDataType.rtComplexArry; if (Sign < 0) { for (int i = 0; i < arr.Length; ++i) arr[i] *= -1.0; } return arr; } default: throw new EquationException("Child equation evaluate error!"); } } public override string ToEquationText() { string txt = "Log(" + Operand.ToEquationText() + ")"; if (Sign < 0) txt = "-" + txt; return txt; } } }
解析器
using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Diagnostics; using System.Text.RegularExpressions; namespace Program { public class EquationBuilder { List<object> tokens = new List<object>(); protected string TokenizeParenthesis(string txt, ref int startpos) { string tok = txt.Substring(startpos, 1); while (tok == " ") // remove leading space { ++startpos; tok = txt.Substring(startpos, 1); } int pos0 = startpos; // position when start int cntLeftParenthesis = 0; if (tok == "(") { ++cntLeftParenthesis; ++startpos; } else { Debug.Assert(txt.StartsWith("(")); return string.Empty; } while (cntLeftParenthesis > 0) { if (startpos >= txt.Length) throw new EquationException("Parenthesis mismatch"); tok = txt.Substring(startpos, 1); ++startpos; if (tok == "(") { ++cntLeftParenthesis; } else if (tok == ")") { --cntLeftParenthesis; } } int pos1 = startpos; // position when finish string str = txt.Substring(pos0, pos1 - pos0); Debug.Assert(!string.IsNullOrWhiteSpace(str)); Debug.Assert(str.StartsWith("(") && str.EndsWith(")")); str = str.Substring(1, str.Length - 2); // remove '(', ')' return str; } protected object Tokenize(string txt, ref int startpos) { // () + - * / string tok = txt.Substring(startpos, 1); switch (tok) { case " ": { ++startpos; return null; } case "(": { string str = TokenizeParenthesis(txt, ref startpos); EquationBuilder bd = new EquationBuilder(); // recursive Equation operand = bd.Build(str); EquParenthesis equ = new EquParenthesis() { Operand = operand }; return equ; } case "+": case "-": case "*": case "/": { ++startpos; return tok; } } // functions if (startpos + 3 < txt.Length) { tok = txt.Substring(startpos, 3); if (tok.ToUpper() == "LOG") { startpos += 3; String str = TokenizeParenthesis(txt, ref startpos); if (string.IsNullOrWhiteSpace(str)) throw new EquationException(string.Format("Invalide argurment of function '{0}'", tok)); EquationBuilder bd = new EquationBuilder(); // recursive Equation operand = bd.Build(str); EquFunction equ = new EquFunction() { Operand = operand }; return equ; } } // dut data // ... // constants Regex reg = new Regex(@"^(\d*\.\d+|\d+|\d+\.\d*)"); tok = txt.Substring(startpos, txt.Length - startpos); Match mt = reg.Match(tok); if (mt.Success) { tok = mt.Value; startpos += tok.Length; EquConstant equ = new EquConstant(Convert.ToDouble(tok)); return equ; } string err = string.Format("Unrecognized string '{0}'", txt.Substring(startpos, txt.Length - startpos)); throw new EquationException(err); } static int OperatorPrecedence(string op1, string op2) { switch (op1) { case "+": case "-": { switch (op2) { case "+": case "-": return 0; case "*": case "/": return -1; default: throw new EquationException("Unrecognized operator " + op2); } } case "*": case "/": { switch (op2) { case "+": case "-": return 1; case "*": case "/": return 0; default: throw new EquationException("Unrecognized operator " + op2); } } default: throw new EquationException("Unrecognized operator " + op1); } } static Equation Build(Equation left, Equation right, string op) { switch (op) { case "+": return new EquAddition() { LeftOperand = left, RightOperand = right }; case "-": return new EquSubtraction() { LeftOperand = left, RightOperand = right }; case "*": return new EquMultiplication() { LeftOperand = left, RightOperand = right }; case "/": return new EquDivision() { LeftOperand = left, RightOperand = right }; default: throw new EquationException("Unrecognized operator " + op); } } public Equation Build(string txt) { // clear leading space txt = txt.Trim(); // if the text is "( ... )" if (txt.StartsWith("(") && txt.EndsWith(")")) { txt = txt.Substring(1, txt.Length - 2); Debug.Assert(false); } // example: txt = "-3 + 4 * (2 / -log( 1 - 5 ))" // tokenize it to top level segments int pos = 0; while (pos < txt.Length) { object obj = Tokenize(txt, ref pos); if (obj != null) tokens.Add(obj); } // example: tokens should be {-, 3, +, 4, equ} // bring '-' into equation if there is one for (int i = tokens.Count - 1; i >= 0; --i) { object o = tokens[i]; if (o is Equation) { if (i >= 2 && (tokens[i - 1] is string) && (tokens[i - 2] is string)) { string str2 = tokens[i - 2] as string; string str1 = tokens[i - 1] as string; Equation equ = o as Equation; if (str1 == "-") { equ.MultiplyMinusOne(); tokens.RemoveAt(i - 1); } else { string err = string.Format("Lack of operand between operators '{0}{1}'", str2, str1); throw new EquationException(err); } } else if (i == 1 && (tokens[i - 1] is string)) { string str1 = tokens[0] as string; Equation equ = o as Equation; if (str1 == "-") { equ.MultiplyMinusOne(); tokens.RemoveAt(i - 1); } else { string err = string.Format("Lack of operand before '{0}{1}'", str1, equ.ToEquationText()); throw new EquationException(err); } } } } // example: tokens now should be {-3, +, 4, equ(modified in inner recursive)} // check, now the tokens should be like {equ, operator, equ, operator, ..., operator, equ} bool beEqu = true; for (int i = 0; i < tokens.Count; ++i) { object o = tokens[i]; if (beEqu != (tokens[i] is Equation)) { string str1 = string.Empty; if (i - 1 >= 0) { if (tokens[i - 1] is Equation) str1 = (tokens[i - 1] as Equation).ToEquationText(); else str1 = tokens[i - 1] as string; } string str = string.Empty; if (tokens[i] is Equation) str = (tokens[i] as Equation).ToEquationText(); else str = tokens[i] as string; string str2 = string.Empty; if (i + 1 < tokens.Count) { if (tokens[i + 1] is Equation) str2 = (tokens[i + 1] as Equation).ToEquationText(); else str2 = tokens[i + 1] as string; } string err = string.Format("Lack of operands/operators '{0}{1}{2}'", str1, str, str2); throw new EquationException(err); } beEqu = !beEqu; } if (tokens[tokens.Count - 1] is string) { throw new EquationException("Lack of operand at the end"); } // build the tree according precedence Stack<string> opStack = new Stack<string>(); Stack<Equation> eqStack = new Stack<Equation>(); for (int i = 0; i < tokens.Count; ++i) { object o = tokens[i]; if (o is Equation) { eqStack.Push(o as Equation); } else if (o is string) { string op = o as string; if (opStack.Count == 0) { opStack.Push(op); } else { // if new add operator is less precedence, build previous first while (true) { string op0 = opStack.Peek(); if (OperatorPrecedence(op, op0) < 0) { Equation right = eqStack.Pop(); Equation left = eqStack.Pop(); Debug.Assert(left != null && right != null); op0 = opStack.Pop(); Equation equ = Build(left, right, op0); eqStack.Push(equ); if (opStack.Count == 0) break; } else { break; } } // then, still push the new operator in opStack.Push(op); } } } while (opStack.Count > 0) { Equation right = eqStack.Pop(); Equation left = eqStack.Pop(); string op = opStack.Pop(); Equation equ = Build(left, right, op); eqStack.Push(equ); } Debug.Assert(eqStack.Count == 1); Equation equResult = eqStack.Pop(); return equResult; } } }
例子:
using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Program { class Program { static void Main(string[] args) { string txt = "-3 + 4 * (2 / -log( 1 - 5 ))"; //string txt = "3 + 4"; EquationBuilder bd = new EquationBuilder(); Equation equ = bd.Build(txt); Console.WriteLine(equ.ToEquationText()); Console.Read(); } } }