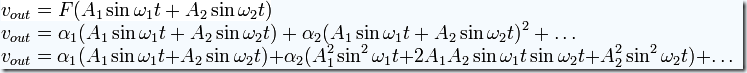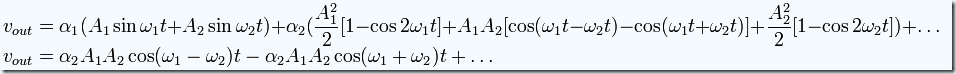外差法 Heterodyne

Read in Wikipedia

-

Mathematical principle

Heterodyning is based on the trigonometric identity:

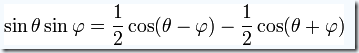
The result is the sum of two sinusoidal signals, one at the sum f₁ + f₂ and one at the difference f₁ - f₂ of the original frequencies

The two signals are multiplied in the mixer. In order to multiply the signals, the mixer must be a nonlinear component, that is, its output current or voltage must be a nonlinear function of its input. Most circuit elements in communications circuits are designed to be linear. This means they obey the superposition principle; if F(v) is the output of a linear element with an input of v:

So if two sine wave signals are applied to a linear device, the output is simply the sum of the outputs when the two signals are applied separately, with no product terms. So the function F must be nonlinear. Examples of nonlinear components that are used as mixers are vacuum tubes and transistors biased near cutoff (class C), and diodes. For lower frequencies, IC analog multipliers can be used which multiply signals precisely. Ferromagnetic core inductors driven into saturation can also be used. In nonlinear optics, crystals that have nonlinear characteristics are used to mix laser light beams to create heterodynes at optical frequencies.

To demonstrate mathematically how a nonlinear component can multiply signals and generate heterodyne frequencies, the nonlinear function F can be expanded in a power series (MacLaurin series):

To simplify the math, the higher order terms above α₂ will be indicated by an ellipsis (". . .") and only the first terms will be shown. Applying the two sine waves at frequencies ω₁ = 2πf₁ and ω₂ = 2πf₂ to this device:

It can be seen that the second term above contains a product of the two sine waves. Simplifying with trigonometric identities:

So the output contains sinusoidal terms with frequencies at the sum ω₁ + ω₂ and difference ω₁ - ω₂ of the two original frequencies. It also contains terms at the original frequencies and at multiples of the original frequencies 2ω₁, 2ω₂, 3ω₁, 3ω₂, etc.; the latter are called harmonics. These unwanted frequencies, along with the unwanted heterodyne frequency, must be filtered out of the mixer output to leave the desired heterodyne.

-

1，利用了三角函数的特性

2，使用非线性器（真空管，晶体管，二极管）件产生MacLaurin级数

3，代入三角函数到MacLaurin级数中，得到外差评率，还有谐波；