leetcode287. Find the duplicate Number

问题描述：

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example 1:

Input: [1,3,4,2,2]
Output: 2

Example 2:

Input: [3,1,3,4,2]
Output: 3

Note:

1. You must not modify the array (assume the array is read only).
2. You must use only constant, O(1) extra space.
3. Your runtime complexity should be less than O(n2).
4. There is only one duplicate number in the array, but it could be repeated more than once.

这道题的要求十分之多，以至于我对它没啥思路，所以我就去参考了大神们的方法，在此只做记录总结。

这道题给你一个长为n+1的数组，里面存了 [1,n]的数字，有且只有一个数字会重复，但是这个数字！它重复的次数！不确定！！！！

也就是说[2,2,2]也是可能存在的。

我一开始以为有且只有一个数字重复并且只重复一次，然后就用求和来算的，还能说些什么，我太天真了：）

然后我们就是要找到这个重复的数字并且返回它，这个时候我就想我可以先排个序然后二分搜索一下，然后它说不可以改变数组 ：）

好吧，那我用哈希表存一下行了吧，它说O(1)的空间复杂度：）

时间复杂度还要小于O(n²)

：）

思路：

这道题仍然可以用二分搜索法来解决，因为有且只有一个数字重复，如果没有数字重复的话，小于等于中点的数字的个数小于n/2，那么说明多出来的数字应该是在大于中点的数字中；若小于中点的数字的个数大于n/2，那么说明多出来的数字应该是在小于中点的数字中。然后我们不断缩小重复数字可能出现的范围，并且最终确定重复数字。此时时间复杂度为O(NlogN)

代码：

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size()-1;
        int low = 1;
        int high = n;
        int mid;
        while(low < high){
            mid = (low + high) / 2;
            int count = 0;
            for(int num : nums){
                if(num <= mid)
                    count++;
            }
            if(count > mid)
                high = mid;
            else
                low = mid+1;
        }
        return low;
    }
};

参考链接：https://blog.csdn.net/wr339988/article/details/53617914

另一种解法：

根据本题特点：长为n+1的数组中存储着[1,n]之间的数字，数字与下标之间存在着映射关系。若将k = nums[k]看为一个操作，我们可以产生一个无环的图：

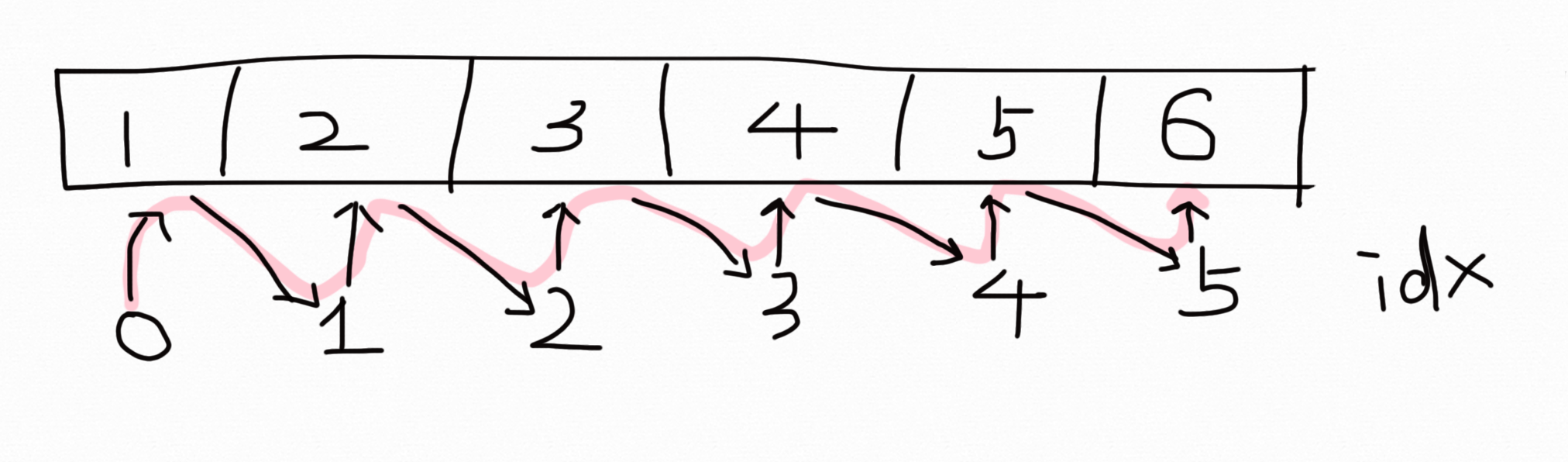
若有重复数字出现，则必定出现环，此时我们可以使用快慢指针来找到相遇点，环的入口则为重复的数字

以图的形式来看：

f为快指针，下标为第几步

可以看见，在第四步时快慢指针相遇。

再找环的入口。

时间复杂度为O(N)

见：找环开始的地方。

代码实现：

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int fast = 0;
        int slow = 0;
        do{
            fast = nums[nums[fast]];
            slow = nums[slow];
        }while(slow != fast);
        fast = 0;
        while(fast != slow){
            fast = nums[fast];
            slow = nums[slow];
        }
        return slow;
    }
};