1192. Critical Connections in a Network

问题描述：

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

 

Example 1:

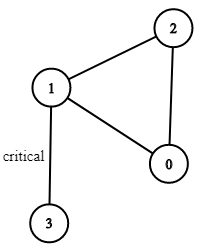
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

 

Constraints:

• 1 <= n <= 10^5
• n-1 <= connections.length <= 10^5
• connections[i][0] != connections[i][1]
• There are no repeated connections.

解题思路：

这道题让我去找图中的桥（bridge)

我一开始的反应是先去找环，然后把构成环的边删除掉，剩下的就是桥。

可是找环也很麻烦，一开始想的是用字符串存储当前路径，并且查找有没有重复，但是这样空间占用多且有可能会出现死循环。

看了网上的解答，还是我对图的了解太少了。。。

这里由ganeshharidas 提供的一些参考资料可以帮我们去了解概念

http://www.cs.cmu.edu/afs/cs/academic/class/15210-f14/www/lectures/graph-dfs.pdf

https://cp-algorithms.com/graph/bridge-searching.html

然后我还找了个视频看了一下：https://www.youtube.com/watch?v=thLQYBlz2DM

主要思想是记录第一次进入这个节点的时间 entryTime[] 和 另外一个标志时间low，我这里也没有想好怎么解释这个数组，我认为是检查是否出现别的路径可以从已经访问过的节点到达该节点标志，这也是我们用来找桥的重要标志。

对每一个节点 i ，但我们第一次访问的时候，用全局变量time赋值给entryTime[i] 和 low[i]， 然后dfs去访问他的孩子节点。

这里需要注意的是，因为是无向图，我们访问的孩子节点不能是它的父亲节点。

对于它的孩子节点 j ，有两种可能：

1. 未访问过

   对孩子节点 j 进行dfs

　对孩子节点j dfs 结束后需要比较entryTime[i] 和 low[j]的关系。如果entryTime[i] < low[j] 则说明，j节点无法连接到i的前继节点，则该边为桥。

2. 访问过

   比较该点的entryTime[j] 和 low[i]， 如果low[i] > entryTime[j], 我们需要更新 low[i] = entryTime[j], 这个时候实际上是出现了back edge，在节点i我们可以有另一条路径到出现时间为j的节点，环就出现了。

 

代码：

class Solution {
public:
    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        vector<vector<int> > adj(n);
        for(auto c : connections){
            adj[c[0]].push_back(c[1]);
            adj[c[1]].push_back(c[0]);
        }
        int time = 0;
        vector<int> entry(n, -1);
        vector<int> low(n, -1);
        vector<vector<int> > ret;
        dfs(0, adj, time, entry, low, ret, -1);
        
        return ret;
    }
private:
    void dfs(int curNode, vector<vector<int> > &g, int &time, vector<int> &entryTime, 
        vector<int> &low, vector<vector<int>> &ret, int parentNode){
        if(entryTime[curNode] == -1){
            entryTime[curNode] = time;
            low[curNode] = entryTime[curNode];
            ++time;
        }
        for(auto &child : g[curNode]){
            if(child == parentNode) continue;
            if(entryTime[child] == -1){
                dfs(child, g, time, entryTime, low, ret, curNode);
                low[curNode] = min(low[curNode], low[child]);
                if(low[child] > entryTime[curNode]){
                    ret.push_back({curNode,child});
                }
            }else{
                low[curNode] = min(low[curNode], entryTime[child]);
            }
        }
    }
};