blender坐标系梳理
一、 目的
理解Blender三维建模软件建模坐标系,obj输出方式,以及与OpenGL坐标系的关系。
二、Blender坐标系解析
0. 建模坐标系
在Blender中, 建模坐标系如下图\((R,F,U)\)(向右,向前,向上)所示:
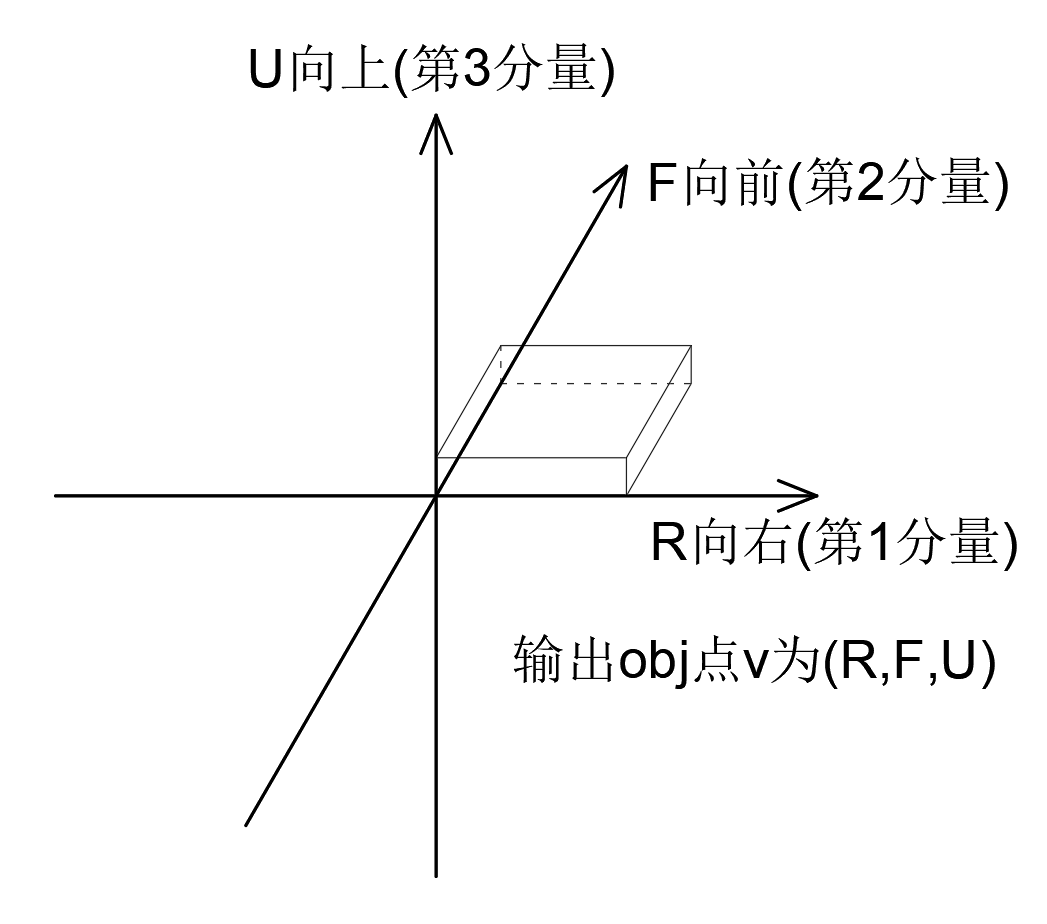
在建模坐标系中, 各轴用列向量方式表示为:
\[R=e_1=\begin{pmatrix}1\\0\\0\end{pmatrix}, F=e_2=\begin{pmatrix}0\\1\\0\end{pmatrix}, U=e_3=\begin{pmatrix}0\\0\\1\end{pmatrix}
\]
1. Blender中obj输出坐标说明
1.0 基本定义
设点在建模坐标系\((R,F,U)\)下的坐标为\(\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}\),在输出坐标系\((X,Y,Z)\)下的坐标为\(\begin{pmatrix}x\\y\\z\end{pmatrix}\),输出坐标系到建模坐标系的转换矩阵为\(M\),则有
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=M\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
\[\begin{pmatrix}x\\y\\z\end{pmatrix}=M^{-1}\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}
\]
1.1 (向上:Z,向前:Y)输出
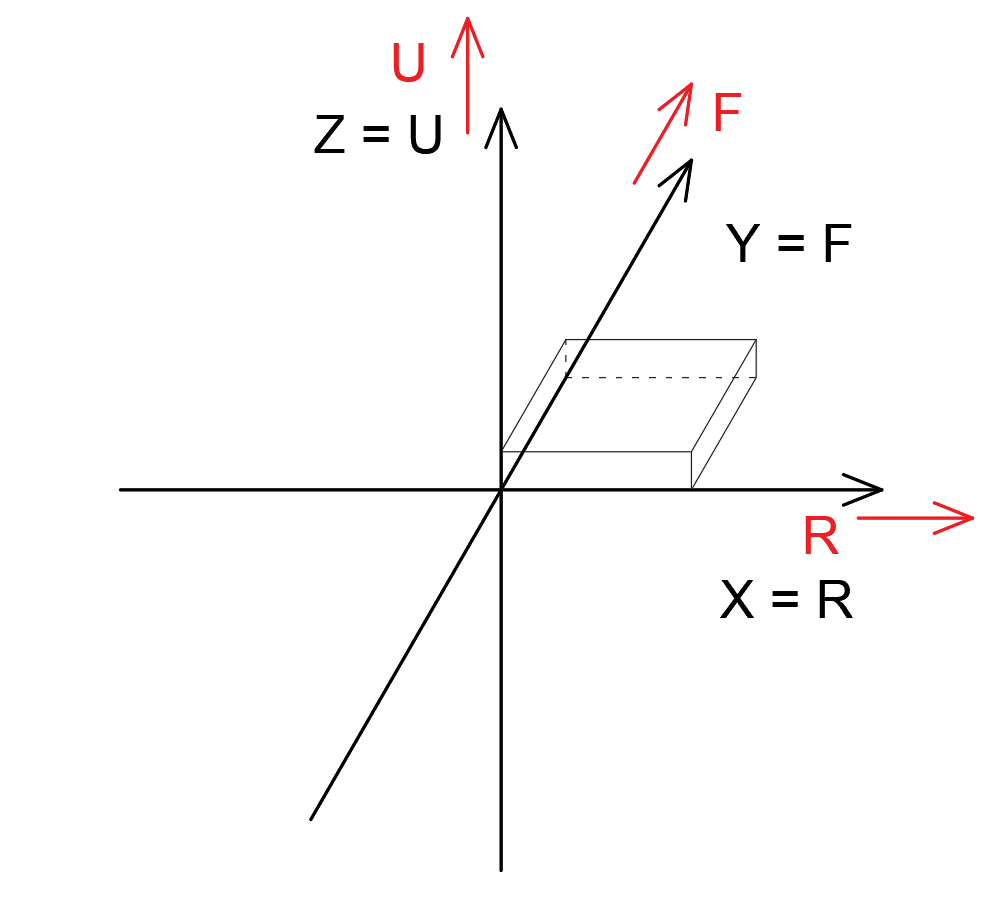
此输出方式下,输出坐标系即为建模坐标系,
\[X=R=e_1, Y=F=e_2, Z=U=e_3
\]
建模坐标\(\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}\)与输出坐标\(\begin{pmatrix}x\\y\\z\end{pmatrix}\)的转换关系为
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=xe_1 + ye_2 + ze_3 = (e_1,e_2,e_3)\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
即
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
转换矩阵及其逆矩阵为
\[M = (e_1,e_2,e_3)=\begin{pmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 &1\end{pmatrix}= E_3
\]
\[M^{-1} = M^T = M = E_3
\]
1.2 (向上: Z,向前: -Y)输出
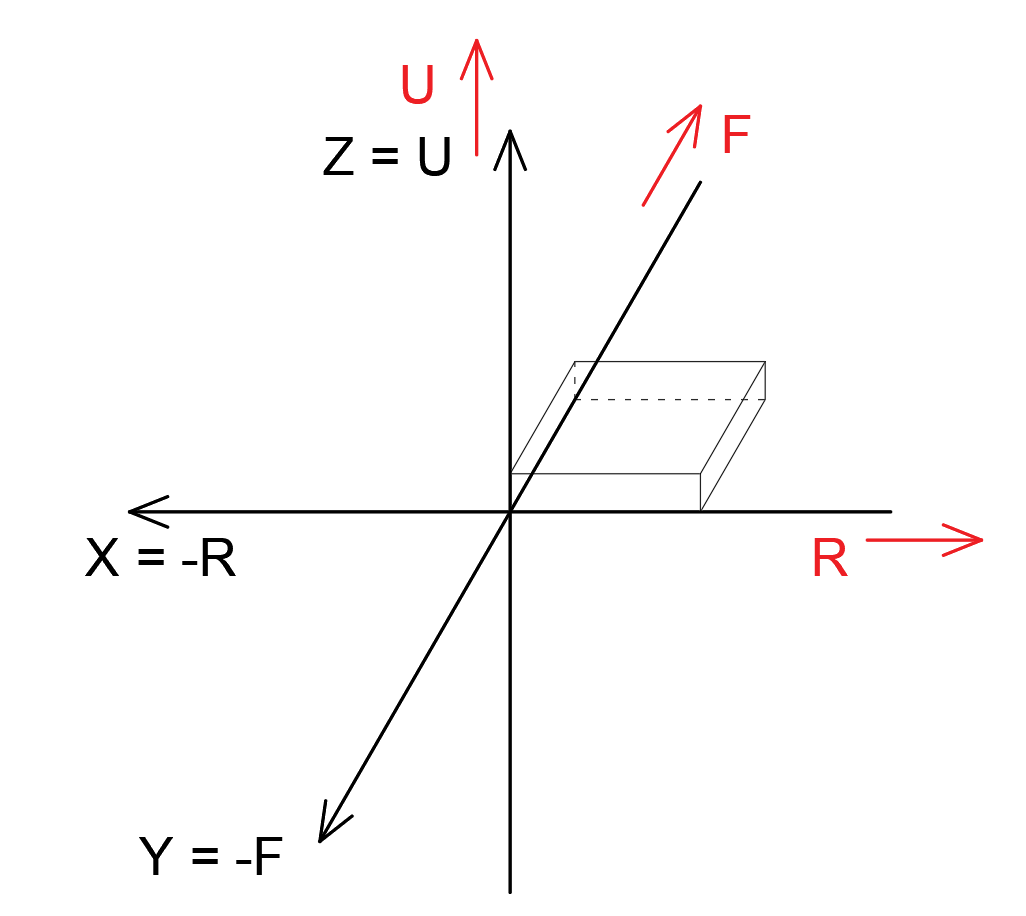
此输出方式中, 输出坐标系轴在建模坐标系中为:
\[X=-R=-e_1, Y=-F=-e_2, Z=U=e_3
\]
建模坐标\(\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}\)与输出坐标\(\begin{pmatrix}x\\y\\z\end{pmatrix}\)的转换关系为
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=x(-e_1) + y(-e_2) + ze_3 =(-e_1,-e_2,e_3)\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
转换矩阵及其逆矩阵为
\[M = (-e_1,-e_2,e_3)=\begin{pmatrix}-1 & 0 & 0\\0 & -1 & 0\\0 & 0 &1\end{pmatrix}
\]
\[M^{-1} = M^T = M
\]
1.3 (向上: Y,向前: -Z)输出(OpenGL坐标系)
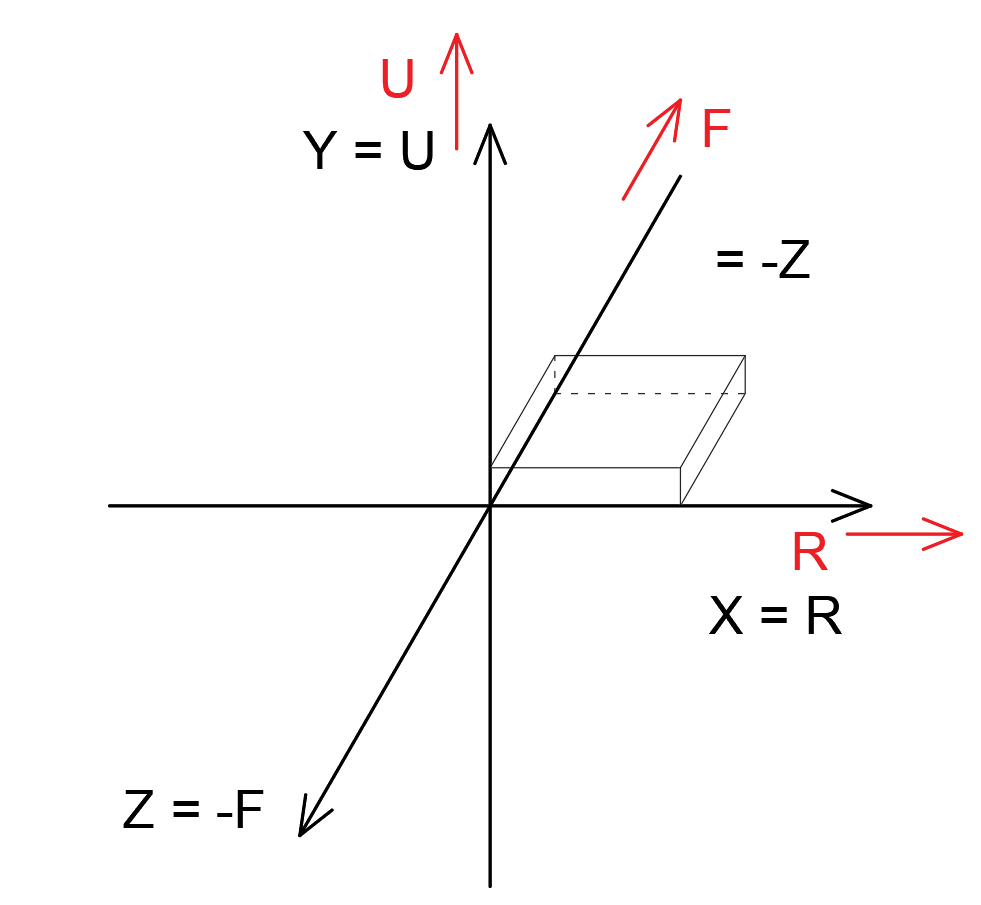
此输出方式中,输出坐标系与建模坐标系的关系为:
\[X=R=e_1, Y=U=e_3, Z=-F=-e_2
\]
建模坐标\(\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}\)与输出坐标\(\begin{pmatrix}x\\y\\z\end{pmatrix}\)的转换关系为
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=x(e_1) + y(e_3) + z(-e_2) =(e_1,e_3,-e_2)\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
转换矩阵及其逆矩阵为
\[M = (e_1,e_3,-e_2)=\begin{pmatrix}1 & 0 & 0\\0 & 0 & -1\\0 & 1 &0\end{pmatrix}
\]
\[M^{-1} = M^T = \begin{pmatrix}1 & 0 & 0\\0 & 0 & 1\\0 & -1 &0\end{pmatrix}
\]
1.4 (向上: Y,向前: Z)
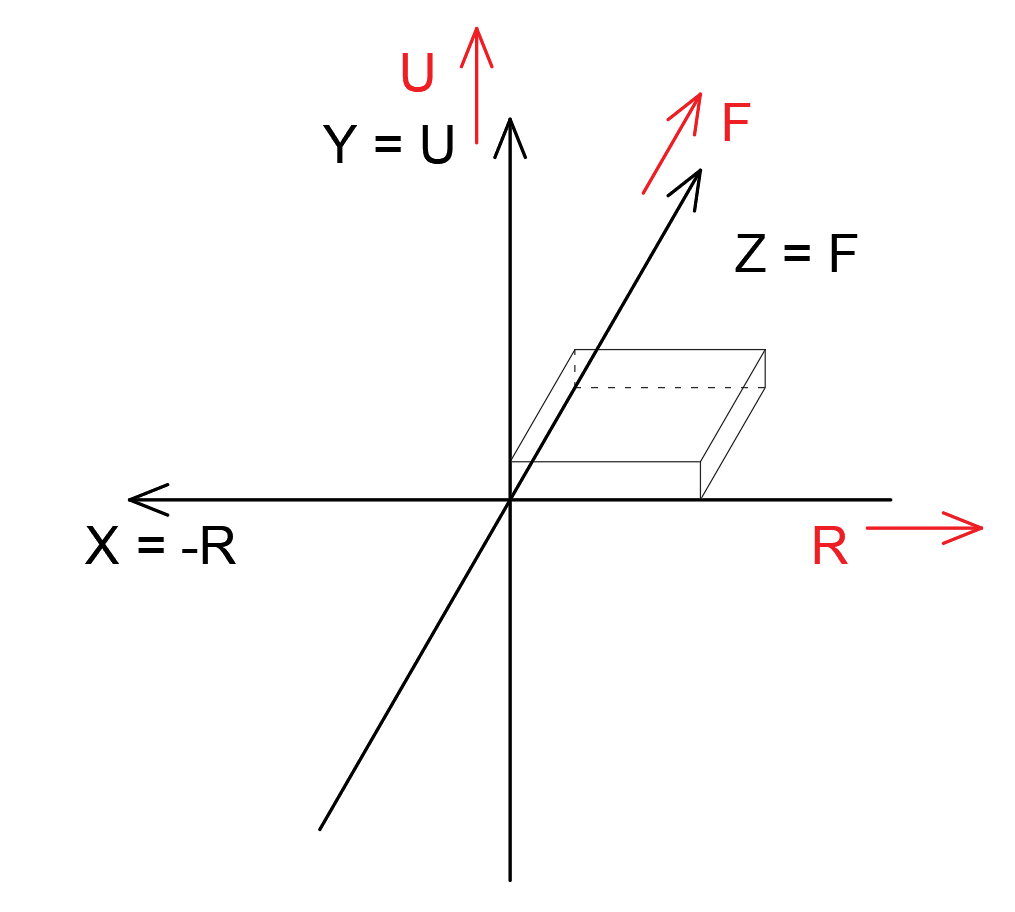
此输出方式中,输出坐标系与建模坐标系的关系为:
\[X=-R=-e_1, Y=U=e_3, Z=F=e_2
\]
建模坐标\(\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}\)与输出坐标\(\begin{pmatrix}x\\y\\z\end{pmatrix}\)的转换关系为
\[\begin{pmatrix}x_o\\y_o\\z_o\end{pmatrix}=x(-e_1) + y(e_3) + z(e_2) =(-e_1,e_3,e_2)\begin{pmatrix}x\\y\\z\end{pmatrix}
\]
转换矩阵及其逆矩阵为
\[M = (-e_1,e_3,e_2)=\begin{pmatrix}-1 & 0 & 0\\0 & 0 & 1\\0 & 1 &0\end{pmatrix}
\]
\[M^{-1} = M^T = M = \begin{pmatrix}-1 & 0 & 0\\0 & 0 & 1\\0 & 1 &0\end{pmatrix}
\]









