过三点的圆
作者: 姚彧
版本历史:
| 版本 | 日期 | 说明 |
|---|---|---|
| 0.1 | 2019-05-28 | 创建文档 |
版权声明:本文为作者原创文章,博客地址:https://www.cnblogs.com/yaoyu126 未经作者允许不得转载。
圆的一般式
\(Ax^2+Ay^2 + Dx + Ey + F = 0 (D^2+E^2-4F>0)\)
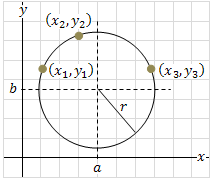
基本性质1, 系数确定
在替换位于圆上的三个给定点之后,我们得到可由行列式描述的方程组:
\(\left|\begin{array}{cccc} x^2+y^2 & x & y & 1\\ x_1^2+y_1^2 & x_1 & y_1 & 1\\ x_2^2+y_2^2 & x_2 & y_2 & 1\\ x_3^2+y_3^2 & x_3 & y_3 & 1 \end{array}\right| = 0\)
系数$ A,B,C和D$可以通过求解以下行列式:
\(A=\left|\begin{array}{cccc} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{array}\right|\)
\(B=-\left|\begin{array}{cccc} x_1^2+y_1^2 & y_1 & 1\\ x_2^2+y_2^2 & y_2 & 1\\ x_3^2+y_3^2 & y_3 & 1 \end{array}\right|\)
\(C=\left|\begin{array}{cccc} x_1^2+y_1^2 & x_1 & 1\\ x_2^2+y_2^2 & x_2 & 1\\ x_3^2+y_3^2 & x_3 & 1 \end{array}\right|\)
\(D=-\left|\begin{array}{cccc} x_1^2+y_1^2 & x_1 & y_1\\ x_2^2+y_2^2 & x_2 & y_2\\ x_3^2+y_3^2 & x_3 & y_3 \end{array}\right|\)
基本性质2, 点与圆位置判断
设\(P(x_p,y_p)\)为任意一点, 在替换位于圆上的三个给定点之后,我们得到行列式:
\(P=\left|\begin{array}{cccc} x^2+y^2 & x & y & 1\\ x_1^2+y_1^2 & x_1 & y_1 & 1\\ x_2^2+y_2^2 & x_2 & y_2 & 1\\ x_3^2+y_3^2 & x_3 & y_3 & 1 \end{array}\right|\) 式1
\(\left\{\begin{aligned} P=0, 在圆上 \\ P>0, 在圆内\\ P<0, 在圆外 \end{aligned}\right.\)
各点平移\((-x_p,-y_p)\)
得新的\(P(0,0)\), \((x_0, y_0), (x_1,y_1), (x_2,y_2)\)代入式1得
\(P=\left|\begin{array}{cccc} 0 & 0 & 0 & 1\\ x_1^2+y_1^2 & x_1 & y_1 & 1\\ x_2^2+y_2^2 & x_2 & y_2 & 1\\ x_3^2+y_3^2 & x_3 & y_3 & 1 \end{array}\right|=\left|\begin{array}{cccc} x_1^2+y_1^2 & x_1 & y_1\\ x_2^2+y_2^2 & x_2 & y_2\\ x_3^2+y_3^2 & x_3 & y_3 \end{array}\right|\) 式2
化简后的计算公式更简单。



