2-3-4树(jdk8的TreeMap的红黑树)
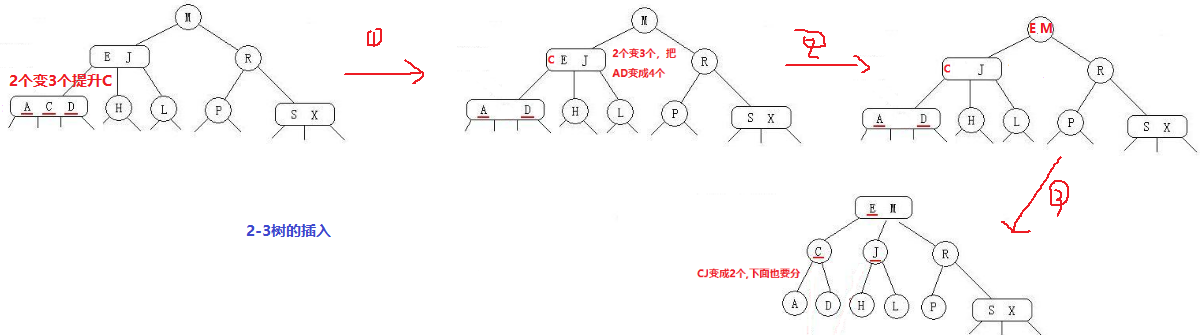
2-3树:插入变成2个节点正常插,变成3个节点就要提升中间节点和分裂子节点,满足:要么没有子节点,要么2个子节点,要么3个子节点。
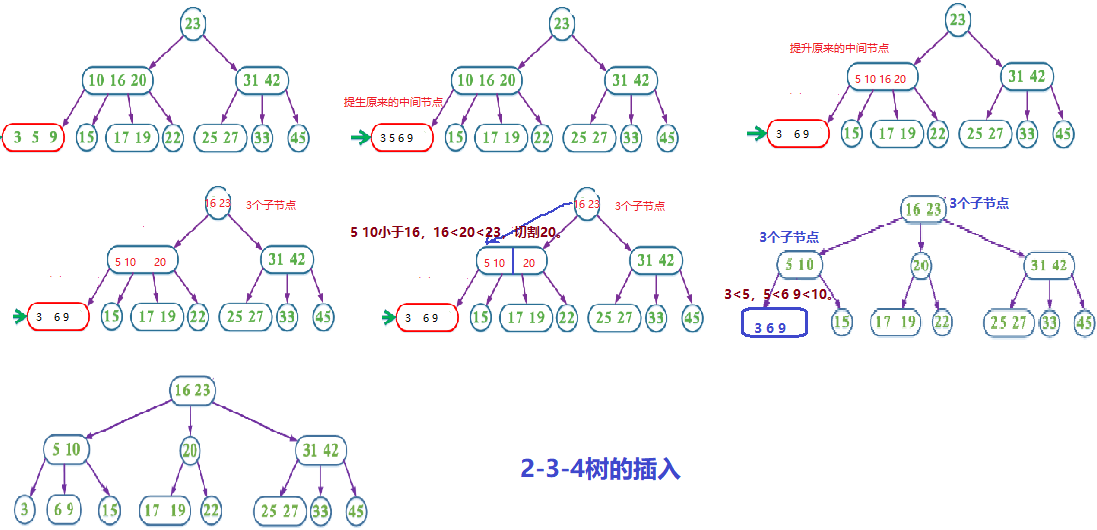
2-3-4树:插入变成2个不动,插入变成3个不动,插入变成4个提升原来中间节点和分裂子节点,满足:要么没有子节点,要么2个子节点,要么3个子节点,要么4个子节点。
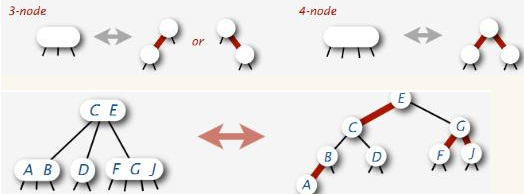
2节点黑色,3节点左倾和右倾,4节点上黑下2红。
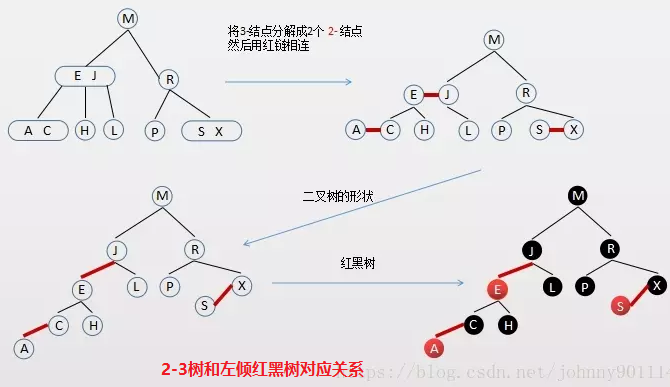
左倾2-3树:2节点黑色,3节点左下红右上黑。
红黑树插入和2-3-4树的对应关系:
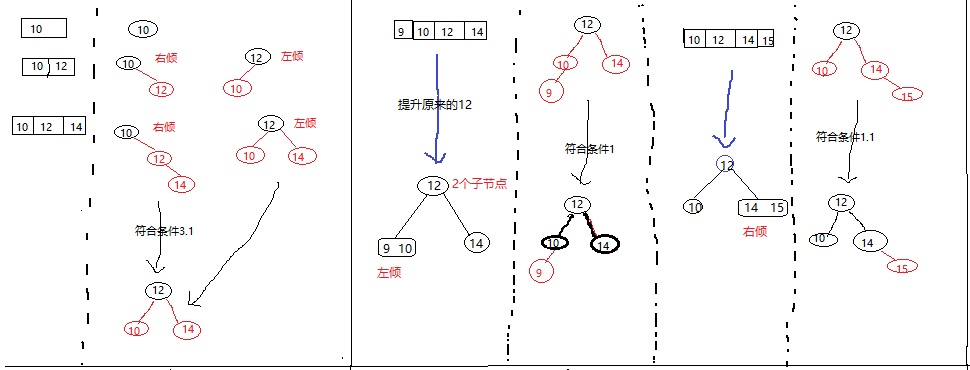
先插入10再插入12,所以是右倾。
先提升12分裂10和14,所以10在12子节点上,在加上9,所以是左倾。 再加上15,因为14在12子节点上,所以是右倾。
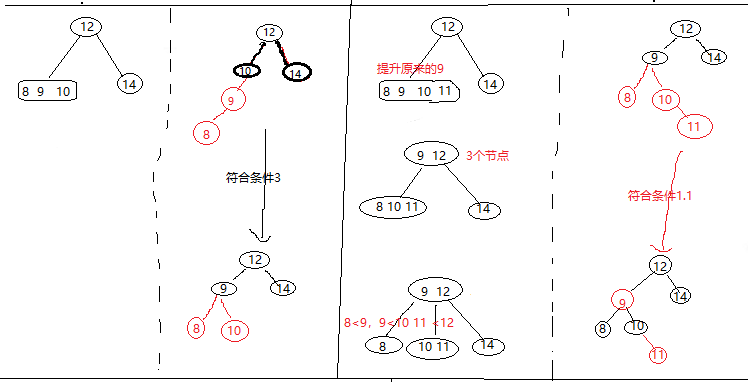
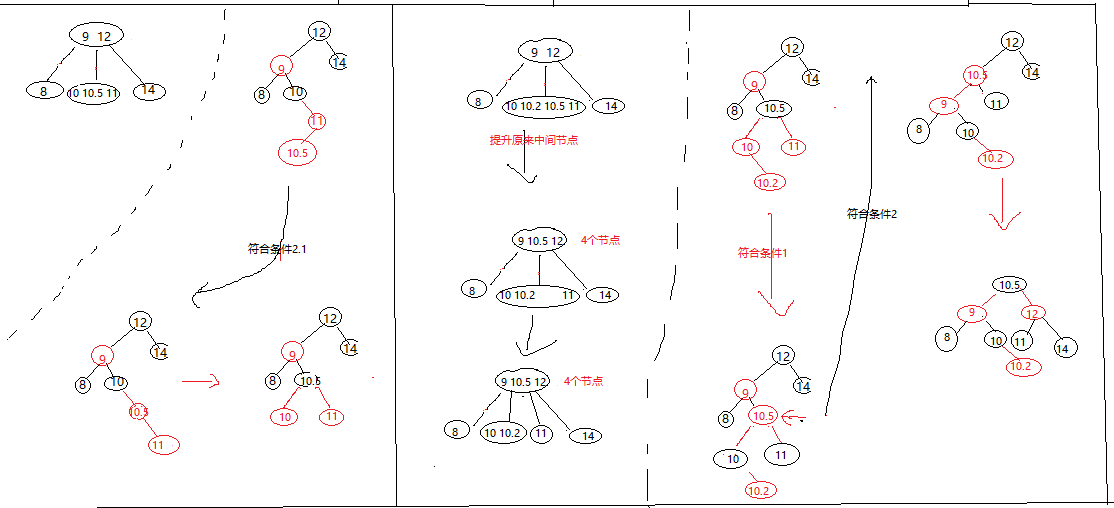
2-3-4树只是规定了普通红黑树最终的样子和颜色,中间调整规则 是通过2-3-4树推到出来的,规则如下:
JDK1.8 TreeMap的红色树插入规则:
1.父亲是黑色,退出
2.父亲是红色
2.1爷爷左边
2.1.1爷爷右节点是红色 条件1
父亲变黑,爷爷右节点变黑,爷爷变红,x指向爷爷继续判断
2.1.2爷爷右节点是黑色
2.1.2.1父亲右边 条件2
左旋父亲 —> 2.1.2.2父亲左边 条件3
父亲变黑,爷爷变红,右旋转爷爷
2.2爷爷右边
2.2.1爷爷左边红色 条件1.1
父亲变黑,爷爷左边变黑,爷爷变红,x指向爷爷继续判断
2.2.2爷爷左边黑色
2.2.2.1父亲左边 条件2.1
右旋转父亲 —> 2.2.2.2父亲右边 条件3.1
父亲变黑,爷爷变红,左旋转爷爷
case 1. 根结点,设为黑色,结束
case 2. 父黑色,不调整,结束
case 3. 叔叔红色,插入节点可左可右:父黑叔叔黑,爷爷红,指向爷爷再看(颜色调整)。
case 4. 叔叔黑色:
父节点左右和爷爷节点左右不在同一边,先旋转父节点到同一边。
父黑爷爷红(颜色调整),反向旋转爷爷。
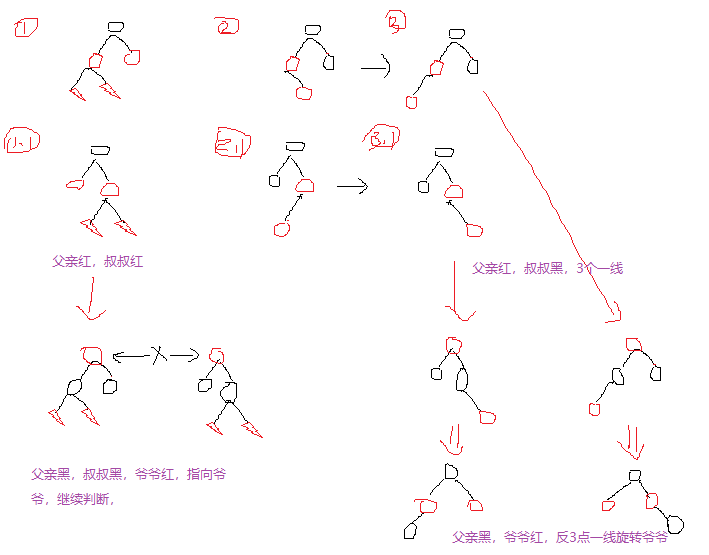
红黑树(对应2-3-4树)和左倾红黑树(对应2-3树)
普通红黑树:允许一个节点有两个红色的子节点
左倾红黑树:一个节点只能有一个红色子节点,并且是左节点
普通红黑树(以下简称红黑树)对应2-3-4树
左倾红黑树对应2-3树
2-3-4树呢?顾名思义,就是有2个子女,3个子女,或4个子女的结点,这些含有2、3、或4个子女的结点就构成了我们的2-3-4树。
一颗红黑树对应唯一形态的2-3-4树,但是一颗2-3-4树可以对应多种形态的红黑树(主要是3节点可以对应两种不同的红黑树形态)
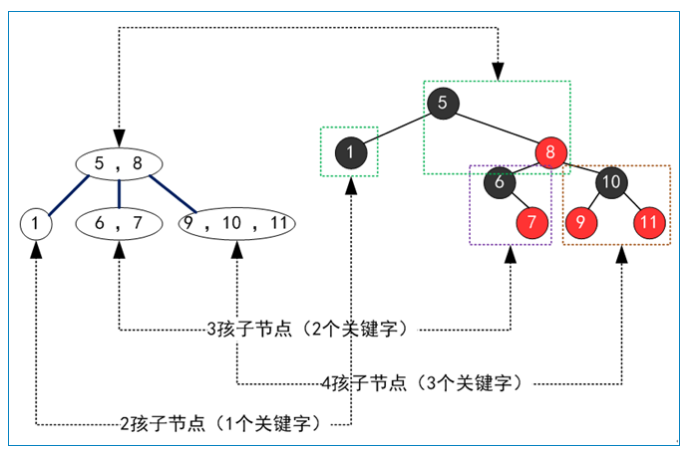
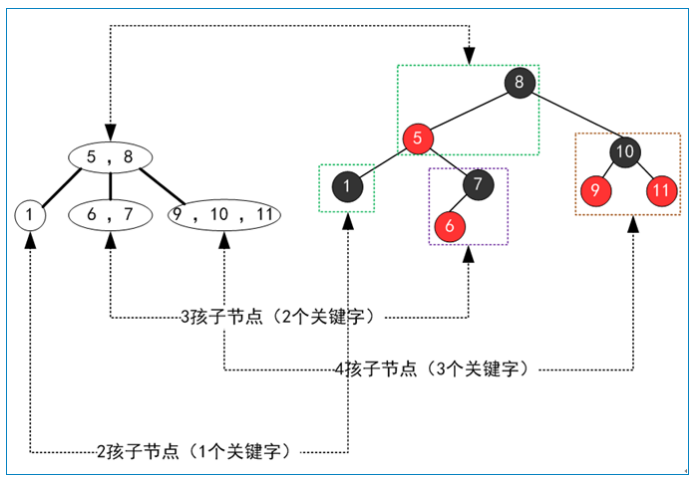
红黑树(普通红黑树,不是左倾红黑树)的五个性质:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(nil)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
左倾红黑树:
- 红链接均为左链接。
- 没有两条红链接相连。
- 任意空链接到根结点的路径上的黑链接数量相同。
传送门:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html