左倾红黑树——左倾2-3树（不是jdk1.8的TreeMap的红黑树）

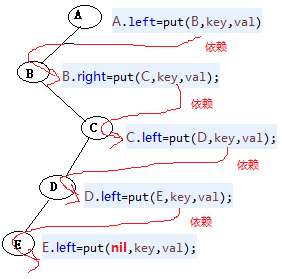
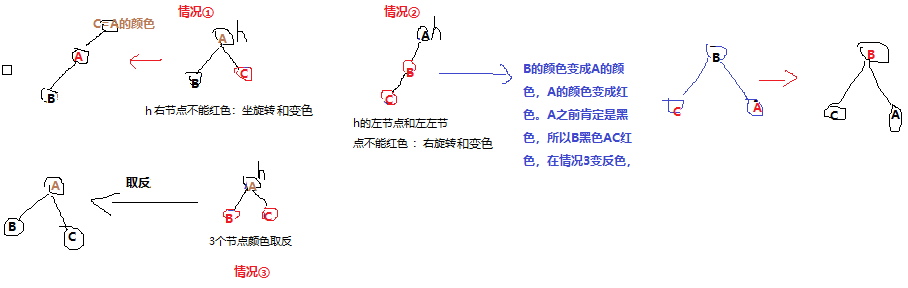
public class RBTree<K extends Comparable<K>, V> {
    public static boolean RED = true;
    public static boolean BLACK = false;
    public Node root;

    class Node {
        K key;
        V val;
        Node left, right;
        boolean color;
        int size;//高度

        Node(K key, V val, boolean color, int size) {
            this.key = key;
            this.val = val;
            this.color = color;
            this.size = size;
        }

        public String toString() {
            return "（K:" + key + " V:" + val + " 色:" + (color==true?"红":"黑") + " s:" + size+ " 左:" + left + " 右:" + right +"）";
        }
    }

    public RBTree() {
    }

    public boolean isRed(Node x) {
        if (null == x)
            return false;//null是黑色
        return x.color == RED;
    }

    public int size(Node x) {
        if (x == null)
            return 0;
        return x.size;
    }

    public int size() {
        return size(root);
    }

    public boolean isEmpty() {
        return root == null;
    }

    public V get(K key) {
        if (key == null)
            throw new IllegalArgumentException();
        return get(root, key);
    }

    public V get(Node n, K key) {
        while (n != null) {
            if (key.compareTo(n.key) == 0)
                return n.val;
            else if (key.compareTo(n.key) < 0)
                n = n.left;
            else
                n = n.right;
        }
        return null;
    }

    private Node rotateLeft(Node h) {
        Node x = h.right;
        h.right = x.left;//节点重挂
        x.left = h;//旋转
        x.color = x.left.color;
        x.left.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

    private Node rotateRight(Node h) {//h.left和h.left.left是红色就右旋转h，
        Node x = h.left;
        h.left = x.right;//节点重挂
        x.right = h;//旋转
        x.color = x.right.color;
        x.right.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

    private void flipColors(Node h) {// 颜色翻转
        h.color = !h.color;
        h.left.color = !h.left.color;
        h.right.color = !h.right.color;
    }

    public void put(K key, V val) throws Exception {
        if (key == null || val == null)
            throw new Exception();
        root = put(root, key, val);
        root.color = BLACK;
    }
    
    //红黑树调整是从下到上，比较路上的所有节点，依次调整，不在比较路上的节点不用调整，调整时候看的也只是左右2个子节点。
    private Node put(Node h, K key, V val) {//递归看形参，进去时候依次是5.0 4.0 3.0 2.0 1.0，出来时候是反过来的，依次是1.0搞完然后2.0搞完然后3.0搞完然后4.0然后5.0。
        if (h == null)
            return new Node(key, val, RED, 1);
        int cmp = key.compareTo(h.key);// key < h.key
        if (cmp < 0) {
            // 放到h的左边，返回新的h的左边，因为有可能会翻转什么的，所以返回新的左节点。
            h.left = put(h.left, key, val);
        } else if (cmp > 0) {
            // 放到h的右边，返回新的h的右边，
            h.right = put(h.right, key, val);
        } else {
            h.val = val;
        }
        //每次给h增加左节点或者右节点之后，都要调整节点h。递归从下到上依次调整。
        if (isRed(h.right) && !isRed(h.left))// h的右节点红色，左节点是null或者黑色。节点的右边不能是红色（性质）。
            h = rotateLeft(h);
        if (isRed(h.left) && isRed(h.left.left))
            h = rotateRight(h);
        if (isRed(h.left) && isRed(h.right))
            flipColors(h);

        h.size = size(h.left) + size(h.right) + 1;
        return h;
    }

    public int getHeight() {
        return getHeight(root);
    }

    private int getHeight(Node p) {// 递归：一个函数里面依赖包含另一个函数。
        if (p == null)
            return 0;
        return Math.max(getHeight(p.left), getHeight(p.right)) + 1;
    }

    @SuppressWarnings("unchecked")
    public static void main(String[] args) throws Exception {
        RBTree rb = new RBTree();
        rb.put(5.0, 5.00);
        rb.put(4.0, 4.00);
        rb.put(3.0, 3.00);
        rb.put(3.5, 3.50);
        rb.put(2.9, 2.90);
        rb.put(3.6, 3.60);
        rb.put(3.55, 3.550);
    }
}

左倾红黑树的另一种定义是满足下列条件的二叉查找树：

1. 红链接均为左链接。
2. 没有两条红链接相连。
3. 任意空链接到根结点的路径上的黑链接数量相同。

 

 

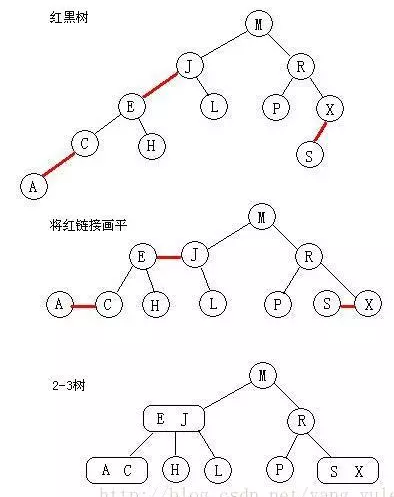
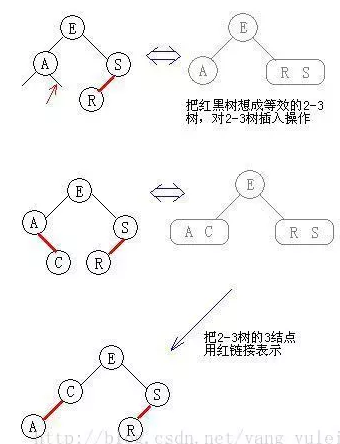
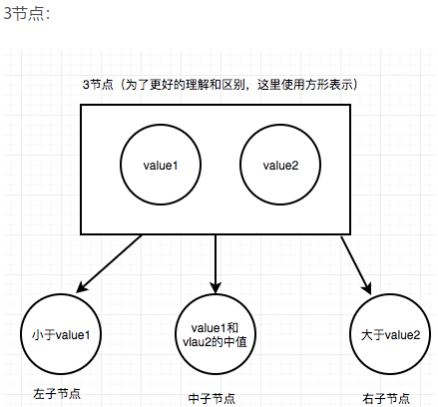
2-3树规定，2节点为黑色，3节点小红大黑，并且父节点链接的是大黑节点。小红在大黑的坐下，中间值节点在小红的右边。

2-3树规定了红黑树最终的样子和颜色，但是中间的旋转和变色过程   是通过2-3树的变换过程推到出来的，规则如下：

 

红黑树就是用红链接表示 3-结点的 2-3 树。

那么红黑树的插入、构造就可转化为 2-3 树的问题，即：在脑中用 2-3 树来操作，得到结果，再把结果中的 3-结点转化为红链接即可。

而 2-3 树的插入，前面已有详细图文，实际也很简单：有空则插，没空硬插，再分裂。 这样，我们就不用记那么复杂且让人头疼的红黑树插入旋转的各种情况了。只要清楚 2-3 树的插入方式即可。

2-3树：2个子节点或者3个子节点。

2-3树是平衡的3路查找树，其中2（2-node）是指拥有两个分支的节点，3（3-node）是指拥有三个分支的节点。B-树是一种平衡的多路查找树，2-3树属于b-树，其也同样具有B-树的性质，如m阶B-树，节点至多有m个分支、m-1个关键字；内部节点的分支数至少为m/2取上限；所有叶节点都出现在同一层次上，并且不带任何信息（这是由构造树的逻辑决定的，实际上指向这些节点的引用为null）。

2-3查找树的定义如下：

1. 要么为空，要么：

2 对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key要小，有节点也是一个2-3节点，所有的值比key要大。

1. 对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

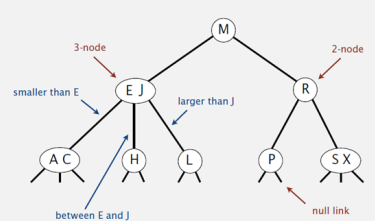
3个子节点根节点就有2个元素，2个子节点根就有一个元素。

永远都是在叶节点处插入新节点，当3-node变为4-node时，需要拆分节点，此时树高就有可能增加。

删除节点比插入节点麻烦一些，先来看删除底部节点，在搜索过程中就需要对节点做相应的变化，以保证搜索路径上的都是3-node或临时的4-node，在删除当前节点T时，T一定是3-node或4-node，就可以安全删除了，删除之后树的变化规则与插入一致。删除其他节点可以转化为删除底部节点，只需要将删除元素与底部节点元素交换即可。

2-3树作为一种平衡查找树，查询效率比普通的二叉排序树要稳定许多，其操作逻辑也非常清晰。2-3树可以采用红黑树实现，使用二叉树结构从逻辑上模拟了2-3树，在插入删除节点时，又具有二叉平衡树的便利。

B-tree树即B树，B即Balanced，平衡的意思。因为B树的原英文名称为B-tree，