堆排序
在堆排序里,很直白的来说,堆就是一个简单的数组。只是我们用一种完全二叉树的角度来看它。以最大堆为例,比如说我们有一棵如下的二叉树:
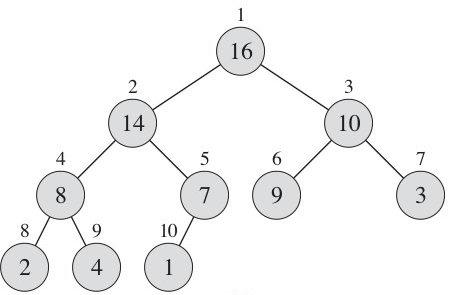
最大堆:跟节点大于左右子节点,左右子节点大小关系是不知道的。
最大堆不是排好序的(只是基本上符合大小关系),要用最大堆排序,就要在最大堆基础上在做处理。每个节点都是以他为根的树的最大的。
如果我们将这种从二叉树的结点关系转换成对应的数组形式的话,则对应的数组如下图:从上到下,从左到右。
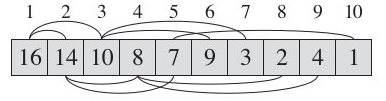
从二叉树的每个结点的编码到它的左右字结点的关系,我们发现一个有意思的地方:左子结点的编号=父结点编号 * 2 ,右子结点的编号=父结点编号 * 2 + 1
按照数组标的编号,有类似的对应关系:左子结点的数组索引号= 父结点索引号 * 2,右子结点的数组索引号=父结点索引号 * 2 + 1
left(n) = n * 2 + 1 right(n) = n * 2 + 2
public static int left(int i) { return i * 2 + 1; } public static int right(int i) { return i * 2 + 2; }
void HeapSort(int a[],int n)//堆排序,输入的序列是数组。输入的数组转换为二叉树是按二叉树从上到下从左到右进行摆放的。 { int t,i; int j;
//将无序的数组构成最大堆 for(i=n/2-1;i>=0;i--) //最后一个非叶节点是n/2-1,从最后一个非也节点开始使得根大于叶子节点 HeapAdjust(a, i, n); //第i个节点为根节点是最大堆,但是还没有按照从小到大排好序。
for(i=n-1;i>0;i--) { t=a[0]; a[0] =a[i]; a[i] =t; //最大堆构建完成之后,元素0就是最大的,取出来放在最后,这样最大的元素下沉了,然后把前面n-1个元素调整为最大堆,把前面n-1个元素最大的移到倒数第二个位置,就是把第二个元素下沉了,一次类推。 HeapAdjust(a,0,i); } } //以s为根节点的二叉树调整为最大堆 void HeapAdjust(int a[],int s,int n) { int j,t; while(2*s+1<n) //有左节点就有右节点 ,是否有左右节点, { j=2*s+1 ;//指向左节点 if((j+1)<n)//存在右节点 { if(a[j]<a[j+1])//右左子树小于右子树,则需要比较右子树 j++; //序号增加1,指向右子树 } if(a[s]<a[j])//比较s与j为序号的数据 { t=a[s]; //交换数据 a[s]=a[j]; a[j]=t; s=j ;//堆被破坏,需要重新调整(如果s是中间节点,s,j交换位置之后,以j为根节点的二叉树有可能现在不满足最大堆),要保证是最大堆。后面利用到第一层最大,第二层第23大这个规律,
} else //比较左右孩子均大则堆未破坏,不再需要调整
break;
}
}
public static void main(String[] args) { int[] a = new int[] {3,5,8,1,80,7,31,9,12,54,89}; HeapSort(a,a.length); }
上面第一个for循环,从最后一个非叶子节点开始,从下到上调整为最大堆(不能从上往下调整)。

然后89和5交换,把最大的移到最后,接着寻找第二大的,
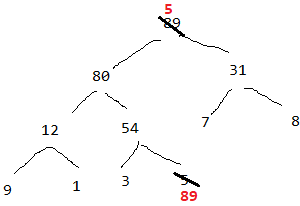
此时不需要从第一个飞叶子节点,从下往上去调整了,只需要调整位置0就可以了(此时可以从上往下调整,因为其余节点满足大堆,交换节点时候,可以保证每次移上去的是最大的,因为最大堆的根节点是整个子树中最大的)。

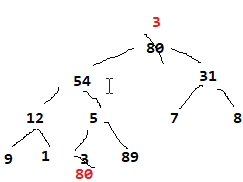
然后又调整节点0.最后:
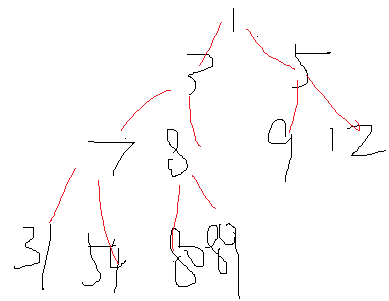
这样,从上到下从左到右就是排好序的数组。
最大堆只是根节点大于子节点,不一定排好序了。

每一次构造最大堆只是找到了最大的元素,然后移除这个最大的,在剩余的里面找第二大的元素。以此类推。
for (int i = 0; i < arrays.length; i++) { //每次建堆就可以排除一个元素了 maxHeapify(arrays, arrays.length - i); //交换 int temp = arrays[0]; arrays[0] = arrays[(arrays.length - 1) - i]; arrays[(arrays.length - 1) - i] = temp; }
/** * 完成一次建堆,最大值在堆的顶部(根节点) */ public static void maxHeapify(int[] arrays, int size) { // 从数组的尾部开始,直到第一个元素(角标为0) for (int i = size - 1; i >= 0; i--) { heapify(arrays, i, size); } }
/** * 建堆 * * @param arrays 看作是完全二叉树 * @param currentRootNode 当前父节点位置 * @param size 节点总数 */ public static void heapify(int[] arrays, int currentRootNode, int size) { if (currentRootNode < size) { //左子树和右字数的位置 int left = 2 * currentRootNode + 1; int right = 2 * currentRootNode + 2; //把当前父节点位置看成是最大的 int max = currentRootNode; if (left < size) { //如果比当前根元素要大,记录它的位置 if (arrays[max] < arrays[left]) { max = left; } } if (right < size) { //如果比当前根元素要大,记录它的位置 if (arrays[max] < arrays[right]) { max = right; } } //如果最大的不是根元素位置,那么就交换 if (max != currentRootNode) { int temp = arrays[max]; arrays[max] = arrays[currentRootNode]; arrays[currentRootNode] = temp; //继续比较,直到完成一次建堆 heapify(arrays, max, size); } } }
树调整成符合条件的最大堆。
一个最简单的办法就是从最低层的结点开始起调整。很明显,如果我们从a[a.length -1]这样的结点来调整的话,有相当一部分结点是没必要的。因为这些结点很显然是叶结点,也就是说他们根本就没有子结点,连找子结点和去比较的必要都没有了。所以,我们可以从最后面往前到过来去找那些有子结点的结点,然后从这些结点开始一个个的进行堆调整。那么,我们该从哪个结点开始起进行调整呢?另外,我们可能还有这么一个疑问,为什么我们要从后面往前去调整?从前面往后调整不行吗?别急,让我们一个个的来分析。
首先第一个问题,从哪个结点开始进行调整。我们来看这棵二叉树,很显然,它最后的一个元素也肯定就是最终的一个叶结点。那么取它的父结点应该就是有子结点的最大号的元素了。那么从它开始就是最合适的。取它的父结点可以通过一个简单的i / 2来得到,i为当前结点的下标。
然后我们再来看第二个问题,为什么要从后往前而不是从前往后。这个相对也比较好理解。我们从下面的层开始调整,保证当上面的父结点来调整的时候,下面的子树已经满足最大堆的条件了。从前往后这么调整的过程不行。不能构成最大堆。
那么,我们如果要从小到大排序的话,最大的元素就只要取根结点就可以了。如果我们把根结点拿走了,放到结果集的最末一个元素,接着就应该找第二大的元素。因为要保证这棵树本身是近似完全二叉树的性质,我们不能把中间的结点直接挪到根结点来比较。但是前面的maxHeapify过程提醒我们,如果我们从集合的最低一层叶结点来取,然后放到根结点进行调整的话,肯定也是可以得到剩下元素里面的最大结点的。就这样,我们可以得到这么一个过程:
1. 取最大堆的根结点元素。
2. 取集合最末尾的元素,放到根结点,调用maxHeapify进行调整。重复步骤1.
在具体实现的时候我们可以发现,每次都要取集合中后面的元素,我们原来得到的最大结点正好可以放到集合的末尾,正好达到最大的元素放到最后的效果。
不能只有右节点没有左节点。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号