2024初秋集训——提高组 #39

B. 启发式图染色问题

题目描述

有这样一个问题：给定一个 $N$ 个点 $M$ 条边的无向图，你要对其中的点进行染色，使得任意边的两个端点颜色不同，求最少颜色数量。

现在你要 hack 以下算法：从前往后贪心的每次将点染成最小需要的颜色，代码如下：

void solve() {
    int n, m;
    std::cin >> n >> m;
    std::vector<int> col(n + 1);
    std::vector<std::vector<int> > g(n + 1);

    for(int i = 1, u, v; i <= m; i ++) {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }

    for(int i = 1; i <= n; i ++) {
        std::set<int> s;
        for(int j : g[i]) 
          if(j < i)
            s.insert(col[j]);
      
        std::vector<int> v(s.begin(), s.end());
        col[i] = v.size() + 1;
        for(int j = 0; j < v.size(); j ++)
            if(v[j] != j + 1) {
                col[i] = j + 1;
                break;
            }
        std::cout << col[i] << " \n"[i == n];
    }
    std::cout << "total = " << *std::max_element(col.begin(), col.end()) << "\n";
}

你要构造一个图，使得你只需要 $c$ 种颜色，而此代码需要 $c+k$ 种颜色。点的数量 $\le 1024$。

思路

我们考虑令 $c=2$ 该怎么构造。

在这张图上每个点都有你的的颜色和错误算法的颜色两种，我们试着先把错误算法凑到 $3$：

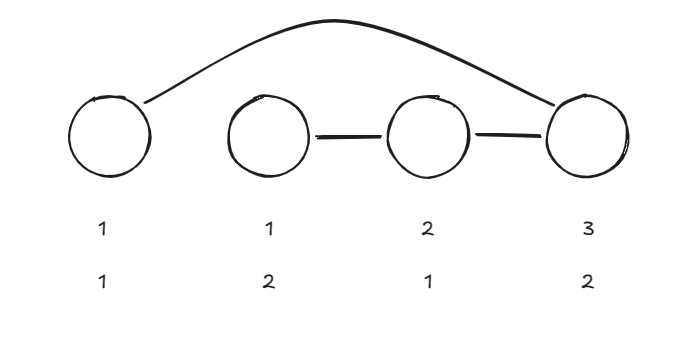
虽然凑到了 $3$，但此时你的颜色为 $2$，也就是不能直接用它跟之前的凑，因为 $1,2$ 凑起来就变成 $3$ 了，所以我们还要构造一个你的颜色为 $1$ 的 $3$，可以把之前 $1,2$ 反过来来凑就行了：

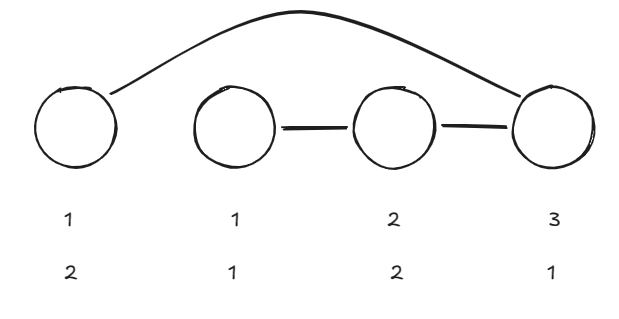
而之前我们凑出来的 $(3,2)$ 继续凑后面的即可。

总之就是对于每种错误算法的颜色，你都要凑出 $1,2$ 两遍，每个点都连向之前的与自己构造的颜色不同的连边。

时空复杂度均为 $O(k^2)$。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 1025;

int k, n;
vector<pii> edge;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> k;
  n = (2 + k) * 2;
  for(int i = 3; i <= n; ++i) {
    for(int j = 1; j < i / 2 * 2; ++j) {
      if((j & 1) ^ (i & 1)) {
        edge.emplace_back(i, j);
      }
    }
  }
  cout << n << " " << edge.size() << " 2\n";
  for(int i = 1; i <= n; ++i) {
    cout << !(i % 2) + 1 << " \n"[i == n];
  }
  for(auto [x, y] : edge) {
    cout << x << " " << y << "\n";
  }
  return 0;
}

C. 自由组队

题目描述

有 $N$ 个人要进行分组，要满足以下条件：

• 每名学生恰好属于一个团队。
• 第 $i$ 名学生属于的团队大小在 $[l_i,r_i]$ 间。

一个大小为 $x$ 的团队的效率为 $w_x$，求分成的团队效率总和最大值。

思路

由于此题 $N\le 60$，且其不关心团队中的人而只关心大小，也就是可以看作一个多重集合，可以证明这样的集合数量是可接受的。所以考虑状压。

我们记录哪些学生已经加入了团队，并从大到小枚举团队大小。我们可以贪心地每次尽可能让 $l$ 更大的进入该团队。状压 dp 即可。

时空复杂度均未知但可过。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 61;

int t, n, l[MAXN], r[MAXN], w[MAXN];
map<ll, int> dp;

void Solve() {
  cin >> n;
  for(int i = 1; i <= n; ++i) {
    cin >> l[i] >> r[i];
  }
  for(int i = 1; i <= n; ++i) {
    cin >> w[i];
  }
  dp.clear();
  dp[0] = 0;
  for(int i = n; i >= 1; --i) {
    map<ll, int> now;
    vector<int> ve;
    for(int j = 1; j <= n; ++j) {
      if(l[j] <= i && r[j] >= i) {
        ve.emplace_back(j);
      }
    }
    sort(ve.begin(), ve.end(), [](int a, int b) -> bool {
      return l[a] > l[b];
    });
    for(auto [s, val] : dp) {
      int res = n - __builtin_popcountll(s), cnt = 0;
      ll k = s;
      if(res < i) {
        continue;
      }
      now[k] = (!now.count(k) ? val : max(now[k], val));
      for(int x : ve) {
        if(!((s >> (x - 1)) & 1)) {
          k |= (1ll << (x - 1));
          if(++cnt == i) {
            cnt = 0;
            now[k] = (!now.count(k) ? (val += w[i]) : max(now[k], (val += w[i])));
          }
        }
      }
    }
    swap(now, dp);
    for(auto [a, b] : now){
      dp[a] = (!dp.count(a) ? b : max(dp[a], b));
    }
  }
  if(dp.count((1ll << n) - 1)) {
    cout << dp[(1ll << n) - 1] << "\n";
  }else {
    cout << "impossible\n";
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  for(cin >> t; t--; Solve()) {
  }
  return 0;
}