CerealCode
GYM 105310 C
题目描述
有 \(N\) 个煎饼店围成一圈,第 \(i\) 个店中有 \(p_i\) 个煎饼。接下来两只红熊猫会进行以下操作:
- 两只熊猫分别选择一个不同的店 \(a,b\)。第一只先选。
- 接着第一个熊猫选择一个不为 \(b\) 的店,从 \(a\) 开始沿着一条不经过 \(b\) 的路线走到该店,并把路径上的店中的煎饼全部吃掉。
- 然后第二个熊猫选择一个没被第一个熊猫经过的店,从 \(b\) 开始沿着一条不经过第一只熊猫经过的店的路线走到该店,并把路径上的店中的煎饼全部吃掉。
两只熊猫都想最大化自己吃的煎饼数量,求第一只熊猫会吃多少个煎饼。
思路
我们考虑枚举 \(a\),并看第二只熊猫会怎么做。
假设此时第二只熊猫已经选好 \(b\) 了,那么此时在第一只熊猫面前有两条路,第一只熊猫肯定会把这条路上能吃的吃完,并且选择煎饼更多的那条。此时第二只就只能吃更少的那条。
所以第二只熊猫得到的煎饼 \(f(b)\) 是一个单峰函数,因为这是两个单调函数的 \(\min\)。我们就可以使用二分,在峰的位置是最后一个 \(f(b)-f(b-1)\ge 0\) 的位置。通过二分出的 \(b\) 就可以求出第一只熊猫的煎饼数。
空间复杂度 \(O(N)\),时间复杂度 \(O(N\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 300001;
int t, n, a[MAXN];
ll sum[MAXN], ans;
ll Calc(int a, int b) {
return min(sum[b] - sum[a], sum[a + n - 1] - sum[b - 1]);
}
int Binary_Search(int x) {
int l = x + 1, r = x + n - 1;
for(; l < r; ) {
int mid = (l + r + 1) >> 1;
(Calc(x, mid) - Calc(x, mid - 1) >= 0 ? l = mid : r = mid - 1);
}
return l;
}
void Solve() {
cin >> n;
for(int i = 1; i <= n; ++i) {
cin >> a[i];
a[n + i] = a[2 * n + i] = a[i];
sum[i] = sum[i - 1] + a[i];
}
for(int i = n + 1; i <= 3 * n; ++i) {
sum[i] = sum[i - 1] + a[i];
}
ans = 0;
for(int i = 1; i <= n; ++i) {
int x = Binary_Search(i);
x -= (x > 2 * n ? 2 : (x > n ? 1 : 0)) * n;
if(x < i) {
ans = max({ans, sum[i] - sum[x], sum[x + n - 1] - sum[i - 1]});
}else {
ans = max({ans, sum[x - 1] - sum[i - 1], sum[i + n] - sum[x]});
}
}
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
for(cin >> t; t--; Solve()) {
}
return 0;
}
GYM 105310 D
题目描述
给定两个字符串 \(s,t\),我们定义字母 \(x\) 的值为其在字母表中的下表(a 为 \(0\))。我们还定义:
- 一个字母 \(x\) 的反转为值为 \(25-x\) 的字母。
- 一个字母 \(x\) 的相对为值为 \((x+13)\bmod 26\) 的字母。
每次你可以将一个区间变成他的反转或相对,求将 \(s\) 变为 \(t\) 的最少次数。如果不行输出 \(-1\)。
思路
推一推便可以发现,先做反转再做相对和先做相对再做反转是一样的,而且这两种操作只有可能做 \(0/1\) 次。
所以令 \(dp_{0/1,0/1,i}\) 表示考虑将前 \(i\) 个字符变相同,最后一个位置是/否做反转,是/否做相对的最少次数。
转移时,如果上一个位置没做反转,但当前做了,那么要多进行一次操作,如果上一个位置没相对,但当前相对了,那么也要多进行一次操作。
时空复杂度均为 \(O(N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1000001, INF = 2 * MAXN;
int n, dp[2][2][MAXN];
string s, t;
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> s >> t;
s = ' ' + s, t = ' ' + t;
for(int i = 0; i <= n; ++i) {
for(bool op : {0, 1}) {
for(bool op2 : {0, 1}) {
dp[op][op2][i] = INF;
}
}
}
dp[0][0][0] = 0;
for(int i = 1; i <= n; ++i) {
for(bool op : {0, 1}) {
for(bool op2 : {0, 1}) {
int x = ((op ? 25 - (s[i] - 'a') : (s[i] - 'a')) + op2 * 13) % 26;
if(x == t[i] - 'a') {
for(bool lop : {0, 1}) {
for(bool lop2 : {0, 1}) {
dp[op][op2][i] = min(dp[op][op2][i], dp[lop][lop2][i - 1] + (op && !lop) + (op2 && !lop2));
}
}
}
}
}
}
int ans = min({dp[0][0][n], dp[0][1][n], dp[1][0][n], dp[1][1][n]});
cout << (ans == INF ? -1 : ans);
return 0;
}
GYM 105310 G
题目描述
有一个 \(N+2\) 行 \(N+2\) 列的网格图,每行,列依次编号 \(0,1,\dots,N+1\)。其中有 \(M\) 个城市,第 \(i\) 个城市位于 \((x_i,y_i)\)。
你将按顺序建造道路:
- 从四个边界中的任意一个边界开始,朝着对面一直修路,直到到达对面或遇到另一条道路。
你不能在边界上修路。
求将这些城市变得连通所需的最小道路总长。
思路
首先第一条道路肯定会贯穿整张图。而接下来的两条道路必定与第一条垂直,就像这样:
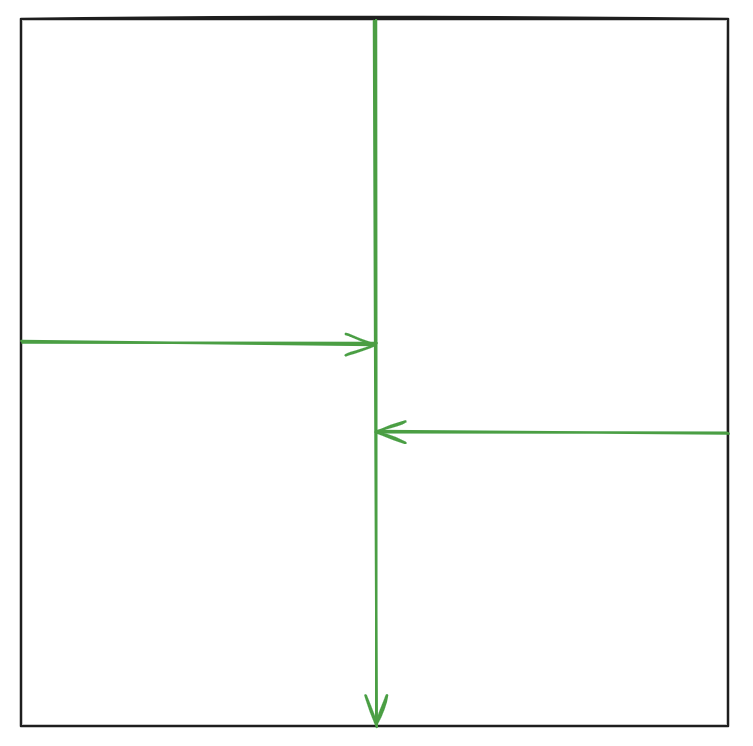
因为要是不是这样,否则就只有可能这样:
而这种情况很明显两边不连通。
所以这样我们就把整张图分成了四块,而每一块上的道路只能连接到对应中间的边界,所以可以用 dp 求解。
时空复杂度均为 \(O(N^2+M)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2005;
int n, m, dp[4][MAXN][MAXN], sum[MAXN][MAXN], maxx[4][MAXN][MAXN], maxy[4][MAXN][MAXN], ans = int(1e9);
int Calc(int x, int y, int x2, int y2) {
return sum[x2][y2] - sum[x - 1][y2] - sum[x2][y - 1] + sum[x - 1][y - 1];
}
void work(int op, int lx, int rx, int ly, int ry, int dx, int dy) {
for(int i = lx; ; i += dx) {
for(int j = ly; ; j += dy) {
maxx[op][i][j] = (dx == 1 ? max({maxx[op][i][j], maxx[op][i - dx][j], maxx[op][i][j - dy]}) : min({maxx[op][i][j], maxx[op][i - dx][j], maxx[op][i][j - dy]}));
maxy[op][i][j] = (dy == 1 ? max({maxy[op][i][j], maxy[op][i - dx][j], maxy[op][i][j - dy]}) : min({maxy[op][i][j], maxy[op][i - dx][j], maxy[op][i][j - dy]}));
if(j == ry) {
break;
}
}
if(i == rx) {
break;
}
}
}
void DP(int op, int lx, int rx, int ly, int ry, int dx, int dy) {
for(int i = lx; ; i += dx) {
for(int j = ly; ; j += dy) {
int x = maxx[op][i - dx][j - dy], y = maxy[op][i - dx][j - dy];
if((dx == 1 ? (x > 0) : (x <= n)) && (dy == 1 ? (y > 0) : (y <= n))) {
dp[op][i][j] = min(dp[op][x][j] + (dy == 1 ? j : n + 1 - j), dp[op][i][y] + (dx == 1 ? i : n + 1 - i));
}
if(j == ry) {
break;
}
}
if(i == rx) {
break;
}
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 0; i <= n + 1; ++i) {
for(int j = 0; j <= n + 1; ++j) {
maxx[1][i][j] = maxx[3][i][j] = maxy[2][i][j] = maxy[3][i][j] = n + 1;
}
}
for(int i = 1, x, y; i <= m; ++i) {
cin >> x >> y;
sum[x][y]++;
maxx[0][x][y] = maxx[1][x][y] = maxx[2][x][y] = maxx[3][x][y] = x;
maxy[0][x][y] = maxy[1][x][y] = maxy[2][x][y] = maxy[3][x][y] = y;
}
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
}
}
work(0, 1, n, 1, n, 1, 1), work(1, n, 1, 1, n, -1, 1), work(2, 1, n, n, 1, 1, -1), work(3, n, 1, n, 1, -1, -1);
DP(0, 1, n, 1, n, 1, 1), DP(1, n, 1, 1, n, -1, 1), DP(2, 1, n, n, 1, 1, -1), DP(3, n, 1, n, 1, -1, -1);
for(int i = 1; i <= n; ++i) {
int Min = int(1e9), Min2 = int(1e9), Min3 = int(1e9), Min4 = int(1e9), pos = 0, pos2 = 0;
for(int j = 1; j <= n; ++j) {
if(Min > dp[0][i][j] + dp[2][i][j] + (Calc(1, 1, i - 1, n) > 0) * i) {
pos = j;
}
Min = min(Min, dp[0][i][j] + dp[2][i][j] + (Calc(1, 1, i - 1, n) > 0) * i);
if(Min2 > dp[1][i][j] + dp[3][i][j] + (Calc(i + 1, 1, n, n) > 0) * (n + 1 - i)) {
pos2 = j;
}
Min2 = min(Min2, dp[1][i][j] + dp[3][i][j] + (Calc(i + 1, 1, n, n) > 0) * (n + 1 - i));
Min3 = min(Min3, dp[0][j][i] + dp[1][j][i] + (Calc(1, 1, n, i - 1) > 0) * i);
Min4 = min(Min4, dp[2][j][i] + dp[3][j][i] + (Calc(1, i + 1, n, n) > 0) * (n + 1 - i));
}
ans = min({ans, n + 1 + Min + Min2, n + 1 + Min3 + Min4});
}
cout << ans;
return 0;
}



