CCO 2019 Day2

Luogu P6680

题目描述

给定一张 \(N\) 个点，\(M\) 条边的无向简单图。

如果存在 \(1\le a<b<c\le N\) 满足存在边 \((a,b),(a,c)\)，并且不存在 \((b,c)\)，则加入边 \((b,c)\)。

求最后的边数。

思路

首先我们可以把边看做从小的连向大的。

通过观察可以发现只有在这种情况下才会建边：

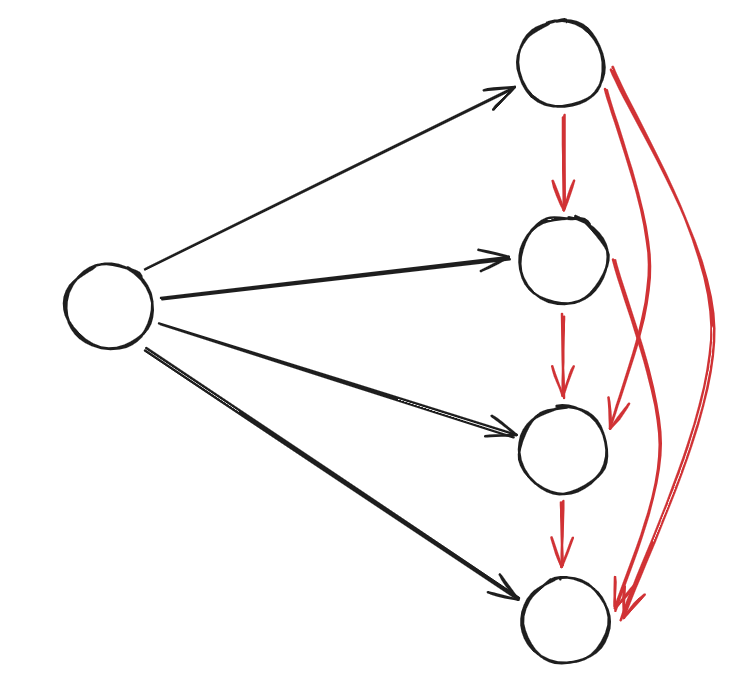
这里红色的边是新加入的。

如果每次我们都对这样的建一个完全图，那么有很多边会被重复加入，所以我们考虑每个点会伸出去多少条边。

可以发现，这里只需要让最靠前的一个儿子建边就行了，也就是这样：

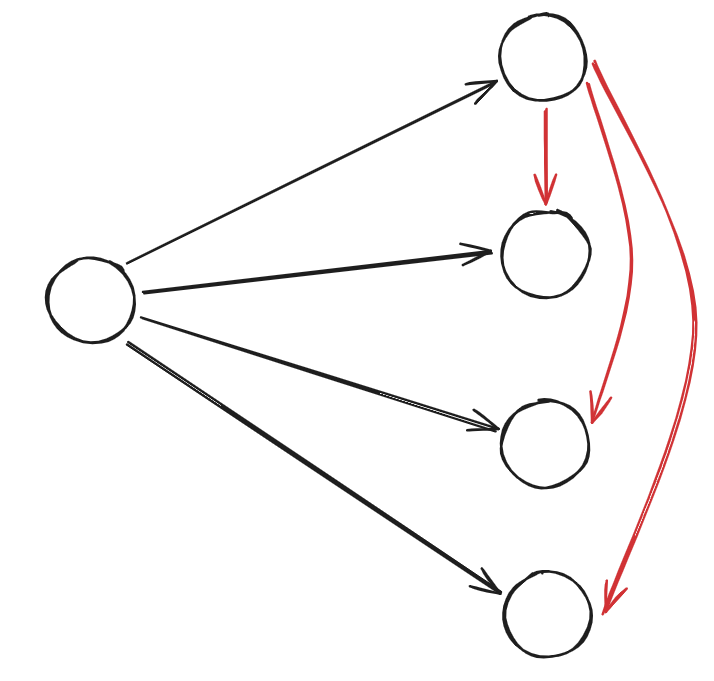
因为在枚举到这个儿子时又会传递给下一个。

所以我们用一个 set 记录连向的结点，然后用启发式合并的方法传递给儿子。

空间复杂度 \(O(N+M)\)，时间复杂度 \(O(N\log^2 M)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 100001;

int n, m;
ll ans;
set<int> e[MAXN];

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].insert(v);
  }
  for(int i = 1; i <= n; ++i) {
    ans += e[i].size();
    if(e[i].size()) {
      int x = *e[i].begin();
      e[i].erase(x);
      if(e[i].size() > e[x].size()) {
        swap(e[i], e[x]);
      }
      for(int v : e[i]) {
        e[x].insert(v);
      }
    }
  }
  cout << ans;
  return 0;
}

Luogu P6681

题目描述

给定 \(N\) 个长度至多为 \(M\) 的 \(01\) 串。你要用两种不同的字符串组合拼接出一个相同的 \(01\) 串，你可以使用重复的字符串。求这个拼接出字符串的最短长度。如果没有输出 \(-1\)。

思路

令 \(dp_S\) 表示更长的字符串比更短的字符串长出的部分为 \(S\) 时的最短长度。

每次我们暴力枚举下一个位置填什么字符串并拼接即可。

空间复杂度 \(O(NM)\)，时间复杂度 \(O(NM(NM+\log NM))\)。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 51;

struct Node {
  string s;
  int dis;
};

struct cmp {
  bool operator()(const Node &a, const Node &b) const {
    return a.dis > b.dis;
  }
};

int n, m;
map<string, int> dist;
map<string, bool> vis;
string s[MAXN];

bool check(const string &a, const string &b) {
  for(int i = 0; i < min(int(a.size()), int(b.size())); ++i) {
    if(a[i] != b[i]) {
      return 0;
    }
  }
  return 1;
}

string Get(const string &a, const string &b) {
  string ret = "";
  for(int i = 0; i < max(int(a.size()), int(b.size())); ++i) {
    if(i >= int(a.size())) {
      ret += b[i];
    }
    if(i >= int(b.size())) {
      ret += a[i];
    }
  }
  return ret;
}

void dij() {
  priority_queue<Node, vector<Node>, cmp> pq;
  for(int i = 1; i <= n; ++i) {
    for(int j = 1; j <= n; ++j) {
      if(i != j && check(s[i], s[j])) {
        string t = Get(s[i], s[j]);
        int w = max(0, int(s[j].size()) - int(s[i].size()));
        if(!dist.count(t) || int(s[i].size()) + w < dist[t]) {
          dist[t] = int(s[i].size()) + w;
          pq.push({t, int(s[i].size()) + w});
        }
      }
    }
  }
  for(; !pq.empty(); ) {
    auto [str, dis] = pq.top();
    pq.pop();
    if(vis.count(str)) {
      continue;
    }
    vis[str] = 1;
    for(int i = 1; i <= n; ++i) {
      if(check(str, s[i])) {
        string t = Get(str, s[i]);
        int w = max(0, int(s[i].size()) - int(str.size()));
        if(!dist.count(t) || dis + w < dist[t]) {
          dist[t] = dis + w;
          pq.push({t, dis + w});
        }
      }
    }
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1; i <= n; ++i) {
    cin >> s[i];
  }
  dij();
  cout << (!dist.count("") ? -1 : dist[""]);
  return 0;
}