李超线段树

有 \(Q\) 次操作，每次操作如下：

• 插入一条直线 \(y=kx+b\)。
• 求在 \(x=k\) 处最大的 \(y\)。

这就是李超线段树解决的问题。

李超线段树就是对 \(x\) 建树，每个点记录其区间中可能为最大值的直线。

这是什么意思呢？我们直接给出过程。

假设要插入直线 \(x\)，从根结点开始，不断执行以下操作直到叶子节点：

• 令 \(mid=\lfloor\frac{l+r}{2}\rfloor\) ，比较 \(x\) 和结点上记录的直线 \(y\) 在 \(mid\) 处哪个大，如果 \(x\) 更大，则交换 \(x,y\)。

• 如果 \(x\) 的斜率 \(>y\) 的斜率，则只有可能在右半区间中 \(x\) 比 \(y\) 大。递归到右边。图如下（假设 \(mid=0\)）：

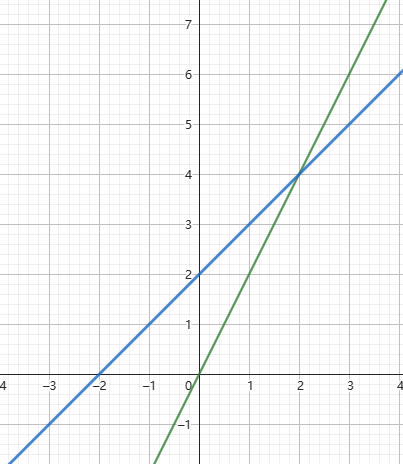
这里蓝色直线在 \(mid\) 处更大，但是在右半区间中绿色直线超过了蓝色直线。

• 同理，若 \(x\) 的斜率 \(<y\) 的斜率，则只有可能在左半区间中 \(x\) 比 \(y\) 大。递归到左边。

• 若 \(x\) 的斜率 \(=y\) 的斜率，则 \(x\) 永远也不可能超过 \(y\)。终止递归。图如下（同样假设 \(mid=0\)）：

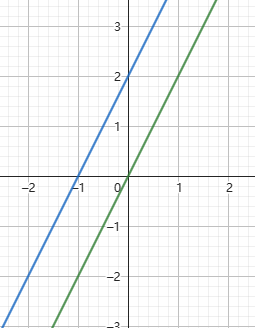
在此图中，蓝色直线永远大于绿色直线。

而查询时只需找出 \(x=k\) 在树上的路径，求所有的最大值即可。

如何插入线段

先找到线段对应的区间，然后使用插入直线一样的方法即可。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 400001;
const ll INF = (ll)(3e18) + 1;

struct line {
  int k;
  ll b;
  ll Get(int x) {
    return 1ll * x * k + b;
  }
};

struct Li_Segment_Tree {
  int tot;
  struct Node {
    int l, r, ls, rs;
    line Min;
  }t[MAXN << 1];
  Li_Segment_Tree(int l, int r) {
    t[tot = 1] = {l, r, 0, 0, line{0, INF}};
  }
  void Insert(line l) {
    int u = 1;
    for(; t[u].l < t[u].r; ) {
      int mid = t[u].l + (t[u].r - t[u].l) / 2;
      if(l.Get(mid) < t[u].Min.Get(mid)) {
        swap(l, t[u].Min);
      }
      if(t[u].l + 1 == t[u].r || l.k == t[u].Min.k || l.b == INF) {
        break;
      }
      if(l.k > t[u].Min.k) {
        if(!t[u].ls) {
          t[u].ls = ++tot, t[tot] = {t[u].l, mid, 0, 0, line{0, INF}};
        }
        u = t[u].ls;
      }else {
        if(!t[u].rs) {
          t[u].rs = ++tot, t[tot] = {mid, t[u].r, 0, 0, line{0, INF}};
        }
        u = t[u].rs;
      }
    }
  }
  ll Getmin(int x) {
    int u = 1, l = -int(1e9), r = int(1e9) + 1;
    ll ret = INF;
    for(; u && t[u].l < t[u].r; ) {
      int mid = l + (r - l) / 2;
      ret = min(ret, t[u].Min.Get(x));
      if(l + 1 == r) {
        break;
      }
      (x < mid ? (u = t[u].ls, r = mid) : (u = t[u].rs, l = mid));
    }
    return ret;
  }
}tr(-(int)(1e9), (int)(1e9) + 1);

int n, q;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> q;
  for(int i = 1, k; i <= n; ++i) {
    ll b;
    cin >> k >> b;
    tr.Insert(line{k, b});
  }
  for(int i = 1, op, k, x; i <= q; ++i) {
    ll b;
    cin >> op;
    if(!op) {
      cin >> k >> b;
      tr.Insert(line{k, b});
    }else {
      cin >> x;
      cout << tr.Getmin(x) << "\n";
    }
  }
  return 0;
}