2024初秋集训——提高组 #22
A. 牛牛的方程式
题目描述
给定一个三元一次方程 \(ax+by+cz=d\),求该方程是否存在整数解。
思路
由于若干个 \(a,b,c\) 只能凑出 \(\gcd (a,b,c)\) 的倍数,所以只需判断 \(d\) 是否为 \(\gcd(a,b,c)\) 的倍数即可。特别的,若 \(a,b,c\) 均为 \(0\),则显然只有 \(d=0\) 时存在整数解。
时空复杂度均为 \(O(1)\)。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int t;
ll a, b, c, d;
ll gcd(ll a, ll b) {
return (!b ? a : gcd(b, a % b));
}
void Solve() {
cin >> a >> b >> c >> d;
cout << (!a && !b && !c ? (!d ? "YES\n" : "NO\n") : (d % gcd(gcd(a, b), c) == 0 ? "YES\n" : "NO\n"));
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
for(cin >> t; t--; Solve()) {
}
return 0;
}
B. 牛牛的猜球游戏
题目描述
有一排 \(10\) 个球,依次编号 \(0-9\),有 \(N\) 种操作,每次操作交换球 \(a,b\)。给定 \(M\) 次查询,每次求依次进行完 \(l\) 到 \(r\) 的操作后每个位置上球的编号。
思路
由于此题没有修改,所以考虑倍增。
令 \(f_{i,j}\) 表示从 \(i\) 开始,进行 \(2^j\) 次操作后每个球所处的位置。
我们很明显有以下转移:\(f_{i,j,_k}=f_{i+2^{j-1},j-1,f_{i,j-1,k}}\)。
查询时直接倍增求解即可。
空间复杂度 \(O(N\log N)\),时间复杂度 \(O(N \log N + M\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 100001;
int n, m, f[18][MAXN][11], res[11], ans[11];
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1, a, b; i <= n; ++i) {
cin >> a >> b;
a++, b++;
for(int j = 1; j <= 10; ++j) {
f[0][i][j] = j;
}
swap(f[0][i][a], f[0][i][b]);
}
for(int i = 1; i <= 17; ++i) {
for(int j = 1; j <= n; ++j) {
if(j + (1 << i) - 1 <= n) {
for(int k = 1; k <= 10; ++k) {
f[i][j][k] = f[i - 1][j + (1 << (i - 1))][f[i - 1][j][k]];
}
}
}
}
for(int i = 1, l, r; i <= m; ++i) {
cin >> l >> r;
for(int j = 1; j <= 10; ++j) {
res[j] = j;
}
int x = l;
for(int j = 17; j >= 0; --j) {
if(x + (1 << j) - 1 <= r) {
for(int k = 1; k <= 10; ++k) {
res[k] = f[j][x][res[k]];
}
x += (1 << j);
}
}
for(int j = 1; j <= 10; ++j) {
ans[res[j]] = j;
}
for(int j = 1; j <= 10; ++j) {
cout << ans[j] - 1 << " \n"[j == 10];
}
}
return 0;
}
C. 牛牛的凑数游戏
题目描述
对于一个多重集合 \(S\),若 \(\exists S' \subseteq S\) 且 \(\sum \limits_{x\in S'} x = v\),则我们说 \(S\) 可以表示 \(v\)。
给定一个长度为 \(N\) 的序列 \(A\) 和 \(M\) 次查询,每次查询若 \(S=\{A_l,A_{l+1},\dots,A_r\}\) 时 \(S\) 最小不能表示的非负整数。
思路
我们先考虑最暴力的一个 dp:
令 \(dp_i\) 表示考虑到第 \(i\) 个数,每个数是/否能表示出。
很明显有 \(dp_{i}=dp_{i-1} \operatorname{or} (dp_{i-1} \operatorname{lsh} A_i)\),这里 \(\operatorname{or},\operatorname{lsh}\) 分别表示位或,左移运算。
由于转移的顺序不会改变结果,所以考虑将 \(A\) 排序。
假设此时 \(dp_i\) 二进制下是 \(X\dots X01\dots 1\),这里令最低位的 \(0\) 在第 \(k\) 位。则在 \(0\) 到 \(k-1\) 位都是 \(1\),所以此时最小不能表示的非负整数为 \(k\)。
现在考虑转移到 \(dp_{i+1}\),此时只要 \(A_{i+1}>k\),则永远也凑不出 \(k\) 了,因为此时左移会跳过 \(k\),又因为 \(A\) 已被排序,所以之后也不会凑出来。此时答案就是 \(k\)。
只要此时没有 \(A_i > k\),我们就能一直加下去。为了加快速度,每次我们让 \(k\leftarrow 小于等于 k 的数字之和\),因为 \(k\) 可以加上所有 \(\le k 且 > lastk\) 的数,这里 \(lastk\) 是上一次的 \(k\)。
而如果 \(k=lastk\),则代表加不下去了,也就是答案为 \(k\)。
但时间复杂度对不对呢?在这里每次至少加上 \(lastk+1\),也就是 \(lastk\) 每次至少 \(\times 2\),那么 \(k\) 也是如此,所以单次时间复杂度 \(O(\log^2 \max\{A_i\})\)。
每次求 \(\le k\) 的数字之和用可持久化 \(01\) 字典树即可。
空间复杂度 \(O(N\log \max \{A_i\})\),时间复杂度 \(O(N\log \max\{A_i\}+M\log^2 \max\{A_i\})\)。
代码
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 100001;
struct Persistent_01Trie {
int tot = 0, ROOT[MAXN], son[2][62 * MAXN];
ll cnt[62 * MAXN];
void Insert(int x, int y, ll val) {
ROOT[x] = ++tot;
int u = ROOT[x], v = ROOT[y];
for(int i = 60; i >= 0; --i) {
son[(val >> i) & 1][u] = ++tot;
son[!((val >> i) & 1)][u] = son[!((val >> i) & 1)][v];
cnt[u] = cnt[v] + val;
u = son[(val >> i) & 1][u], v = son[(val >> i) & 1][v];
}
cnt[u] = cnt[v] + val;
}
ll Getsum(int l, int r, ll val) {
int u = ROOT[l - 1], v = ROOT[r];
ll ans = 0;
for(int i = 60; i >= 0; --i) {
if((val >> i) & 1) {
ans += cnt[son[0][v]] - cnt[son[0][u]], u = son[1][u], v = son[1][v];
}else {
u = son[0][u], v = son[0][v];
}
}
return ans + cnt[v] - cnt[u];
}
}tr;
int n, m;
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1, x; i <= n; ++i) {
cin >> x;
tr.Insert(i, i - 1, x);
}
for(int i = 1, l, r; i <= m; ++i) {
cin >> l >> r;
ll x = 0;
for(; ; ) {
ll last = x;
x = tr.Getsum(l, r, x + 1);
if(x == last) {
break;
}
}
cout << x + 1 << "\n";
}
return 0;
}
D. 牛牛的 RPG 游戏
题目描述
给定一个 \(N\times M\) 的网格图,每个格子 \((i,j)\) 都有一个事件,每次事件如下:
- 获得 \(val(i,j)\) 的分数
- 接下来每走一步都会获得 \(buff(i,j)\) 的分数,直到触发下个事件前都有这个效果。
每遇到一个格子你都能选择是否触发事件,每次你只能往右/下走,求从 \((1,1)\) 开始到 \((N,M)\) 能获得的最大分数。
思路
首先考虑最暴力的 dp:
令 \(dp_{i,j}\) 表示从 \((1,1)\) 到达并触发 \((i,j)\) 的最大分数。
我们有 \(dp_{i,j}\leftarrow dp_{x,y}+(i-x+j-y)\cdot buff(x,y)+val(i,j)\)。
化简一下:\(dp_{i,j}\leftarrow dp_{x,y}-(x+y)\cdot buff(x,y)+(i+j)\cdot buff(x,y)+val(i,j)\)。
这里最难处理的地方就是 \((i+j)\cdot buff(x,y)\),因为它既包含了 \(i,j\) 又包含了 \(x,y\)。
\(val(i,j)\) 可以在最后处理,主要考虑前面的部分。
前面的部分可以看作在平面直角坐标系中一条 \(y=kx+b\) 的直线,这里 \(k=buff(x,y),b=dp_{x,y}-(x+y)\cdot buff(x,y)\),查询时就相当于查询在 \(x=i+j\) 处的最大 \(y\),这个可以用李超线段树求解。
这里考虑分治 dp:
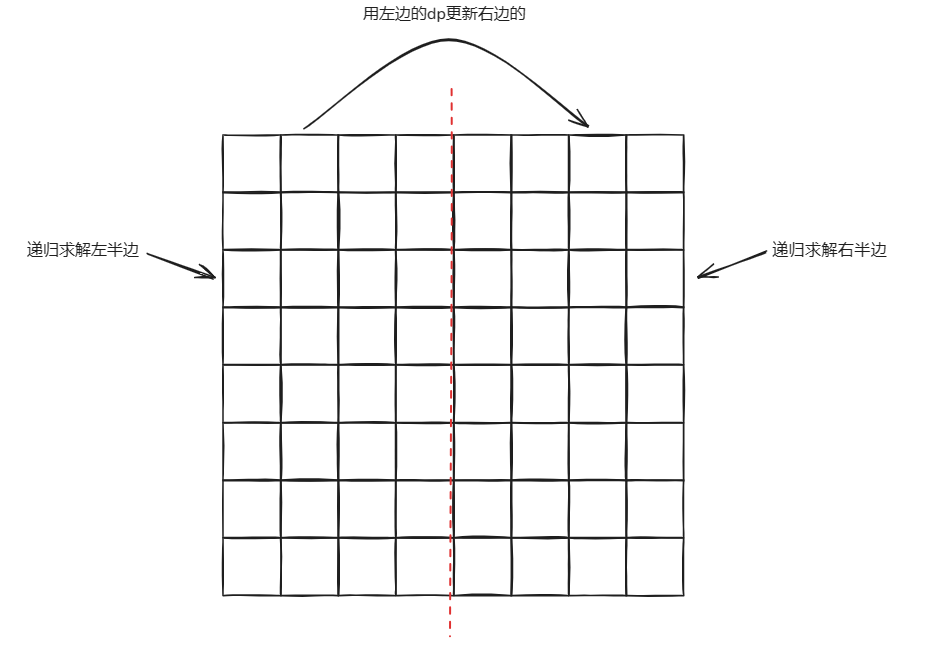
这样不断分治下去,直到只有一列,这样直接 dp,每列只会被访问 \(\log N\) 次,每次时间复杂度 \(O(\log (N+M))\)。
空间复杂度 \(O(NM)\),时间复杂度 \(O(NM \log^2 (N+M))\)。
代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200001, INF = (int)(2e9);
struct line {
int k, b;
int Get(int x) const {
return x * k + b;
}
};
struct Li_Segment_Tree {
int tot;
struct Node {
int l, r, ls, rs;
line Max;
}t[MAXN * 16];
void Clear(int l, int r) {
t[tot = 1] = {l, r, 0, 0, line{0, -INF}};
}
void Insert(line l) {
int u = 1;
for(; t[u].l < t[u].r; ) {
int mid = t[u].l + (t[u].r - t[u].l) / 2;
if(l.Get(mid) > t[u].Max.Get(mid)) {
swap(l, t[u].Max);
}
if(t[u].l + 1 == t[u].r || l.k == t[u].Max.k || l.b == -INF) {
break;
}
if(l.k < t[u].Max.k) {
if(!t[u].ls) {
t[u].ls = ++tot, t[tot] = {t[u].l, mid, 0, 0, line{0, -INF}};
}
u = t[u].ls;
}else {
if(!t[u].rs) {
t[u].rs = ++tot, t[tot] = {mid, t[u].r, 0, 0, line{0, -INF}};
}
u = t[u].rs;
}
}
}
int Getmax(int x) {
int u = 1, l = 1, r = MAXN, ret = 0;
for(; u && t[u].l < t[u].r; ) {
int mid = l + (r - l) / 2;
if(t[u].Max.Get(x) > ret) {
ret = t[u].Max.Get(x);
}
if(t[u].l + 1 == t[u].r) {
break;
}
(x < mid ? (u = t[u].ls, r = mid) : (u = t[u].rs, l = mid));
}
return ret;
}
}tr;
int n, m;
vector<int> b[MAXN], v[MAXN], dp[MAXN];
void dfs(int l, int r) {
if(l == r) {
tr.Clear(1, MAXN);
for(int i = 1; i <= n; ++i) {
dp[i][l] = max(dp[i][l], tr.Getmax(i + l) + v[i][l]);
tr.Insert(line{b[i][l], dp[i][l] - (i + l) * b[i][l]});
}
return;
}
int mid = (l + r) >> 1;
dfs(l, mid);
tr.Clear(1, MAXN);
for(int i = 1; i <= n; ++i) {
for(int j = l; j <= mid; ++j) {
tr.Insert(line{b[i][j], dp[i][j] - (i + j) * b[i][j]});
}
for(int j = mid + 1; j <= r; ++j) {
dp[i][j] = max(dp[i][j], tr.Getmax(i + j) + v[i][j]);
}
}
dfs(mid + 1, r);
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i) {
b[i].resize(m + 1), v[i].resize(m + 1), dp[i].resize(m + 1);
for(int j = 1; j <= m; ++j) {
cin >> b[i][j];
dp[i][j] = -INF;
}
}
dp[1][1] = 0;
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= m; ++j) {
cin >> v[i][j];
}
}
dfs(1, m);
cout << dp[n][m];
return 0;
}



