博弈论

有向图游戏

给定一个有向图，初始在结点 \(s\) 上有一个棋子。两名玩家将轮流移动这个棋子到相邻的一个点上。若有一方不能移动，则另一名玩家获胜。若两方都按最优方案操作，求最终是先手获胜还是后手获胜还是平局。

首先，若当前棋子所在的结点出度为 \(0\)，则先手必败。

很容易想到，若某个状态能转移到一个先手必败状态，则该状态为先手必胜态（这里说某个状态为先手必胜/必败是指棋子从这里开始的结局）。否则若某个状态能转移到一个平局状态，则该状态为平局态。否则该状态为先手必败态。因为此时先手希望自己的结局尽可能更优，也就是让对手的结局尽可能更劣。

所以考虑使用拓扑排序。但这个拓扑排序有点不太一样，我们观察下面这张图：

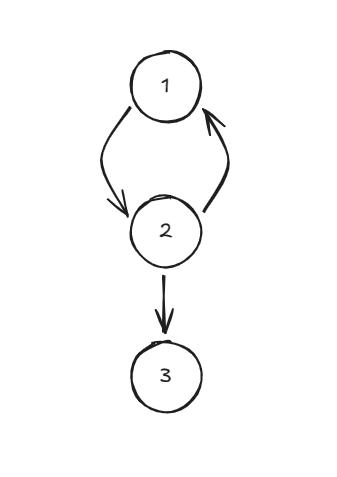
很显然结点 \(3\) 为先手必败态，但上面 \(1\) 和 \(2\) 构成了一个环，所以普通的拓扑排序会认为 \(1\) 和 \(2\) 是平局。而实际上 \(1\) 是先手必败态，\(2\) 是先手必胜态。因为在 \(2\) 上面先手可以选择往 \(3\) 走。所以若某个状态能转移到先手必败态，就直接转移，并且可以无视其他状态。也就相当于将入度清 \(0\)。而最终入度不为 \(0\) 的结点就是平局态。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 200001;

int n, m, in[MAXN], dp[MAXN]; // 0 先手必败  1 平局  2 先手必胜
vector<int> e[MAXN];

void topo_sort() {
  queue<int> que;
  for(int i = 1; i <= n; ++i) {
    if(!in[i]) {
      que.push(i);
    }
  }
  for(; !que.empty(); ) {
    int u = que.front();
    que.pop();
    for(int v : e[u]) {
      if(dp[v] == 2) {
        continue;
      }
      dp[v] = max(dp[v], dp[u]);
      in[v] = (dp[u] == 2 ? 0 : in[v] - 1);
      if(!in[v]) {
        que.push(v);
      }
    }
  }
  for(int i = 1; i <= n; ++i) {
    if(in[i]) {
      dp[i] = 1;
    }
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m >> s;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[v].push_back(u);
    in[u]++;
  }
  topo_sort();
  cout << (!dp[s] ? "lose" : (dp[s] == 1 ? "draw" : "win"));
  return 0;
}

AT ABC261 H

题目描述

给定一个有向带权图，两个人在玩一个游戏。

一开始在点 \(v\) 上有一个棋子，两个人将轮流移动这个棋子。

• 先手会尽可能让游戏不要无限进行。在此基础上，他想最小化经过的边权之和。
• 后手会尽可能让游戏无限进行。在此基础上，他想最大化经过的边权之和。

求最后游戏会不会无限进行。如果会，输出 INFINITY。否则输出经过的边权之和。

思路

由于先后手的目标不同，所以分开dp。

令 \(dp_{u,0/1}\) 表示一开始棋子在 \(u\)，接下来先/后手下时的边权之和。

而 \(dp_{u,0}\) 是求最小值，\(dp_{u,1}\) 是求最大值。也就是一个最短路，一个最长路。

但他们之间又要互相转移，所以就是最短路最长路一起做。

最短路用 dijkstra，最长路用拓扑排序。两个代码合起来就行了。

空间复杂度 \(O(N+M)\)，时间复杂度 \(O((N+M)\log N)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
using ll = long long;

const int MAXN = 200001;
const ll INF = (ll)(1e16);

struct Node {
  int u;
  ll dis;
};

struct cmp {
  bool operator()(const Node &a, const Node &b) const {
    return a.dis > b.dis;
  }
};

int n, m, s, in[MAXN];
bool vis[MAXN];
ll dp[MAXN][2];
vector<pii> e[MAXN];

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m >> s;
  for(int i = 1, u, v, w; i <= m; ++i) {
    cin >> u >> v >> w;
    in[u]++;
    e[v].push_back({u, w});
  }
  for(int i = 1; i <= n; ++i) {
    dp[i][0] = INF;
  }
  queue<int> que;
  priority_queue<Node, vector<Node>, cmp> pq;
  for(int i = 1; i <= n; ++i) {
    if(!in[i]) {
      dp[i][0] = 0;
      pq.push({i, 0});
      que.push(i);
    }
  }
  for(; !que.empty() || !pq.empty(); ) {
    for(; !que.empty(); ) {
      int u = que.front();
      que.pop();
      for(auto [v, w] : e[u]) {
        if(dp[u][1] + w < dp[v][0]) {
          dp[v][0] = dp[u][1] + w;
          pq.push({v, dp[v][0]});
        }
      }
    }
    vector<int> ve;
    for(; !pq.empty(); ) {
      auto [u, dis] = pq.top();
      pq.pop();
      if(vis[u]) {
        continue;
      }
      vis[u] = 1;
      ve.push_back(u);
      for(auto [v, w] : e[u]) {
        dp[v][1] = max(dp[v][1], dp[u][0] + w);
        if(!(--in[v])) {
          que.push(v);
        }
      }
    }
    for(int x : ve) {
      vis[x] = 0;
    }
  }
  if(dp[s][0] == INF) {
    cout << "INFINITY";
  }else {
    cout << dp[s][0];
  }
  return 0;
}