线段树优化建图
首先看这个问题:
一张
- 建
- 建
- 建
求建完边后从
直接暴力建边肯定是无法接受的,所以我们使用线段树的思想试一试,先建一棵线段树,但这棵树是外向的:
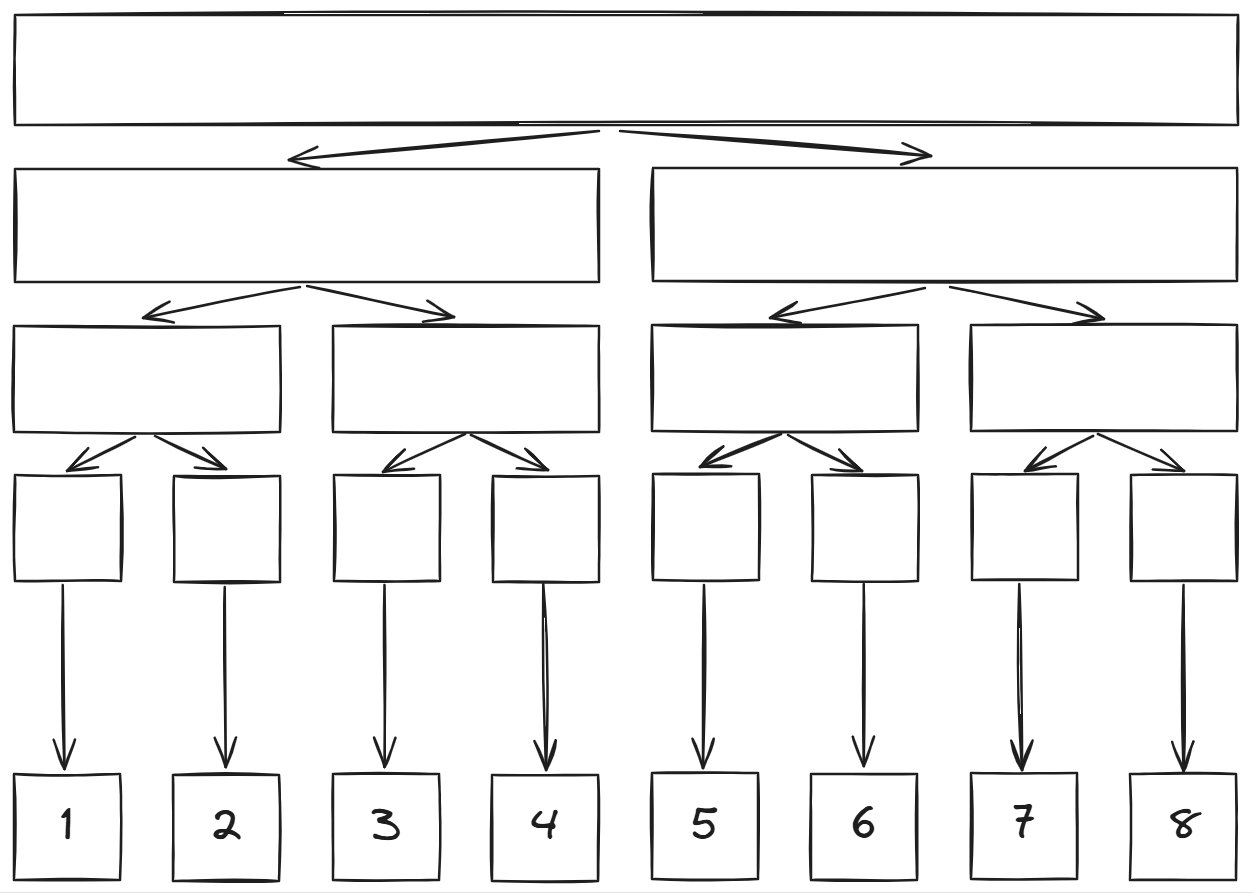
这时可以发现,所有询问的区间均可拆成
但这只能解决第
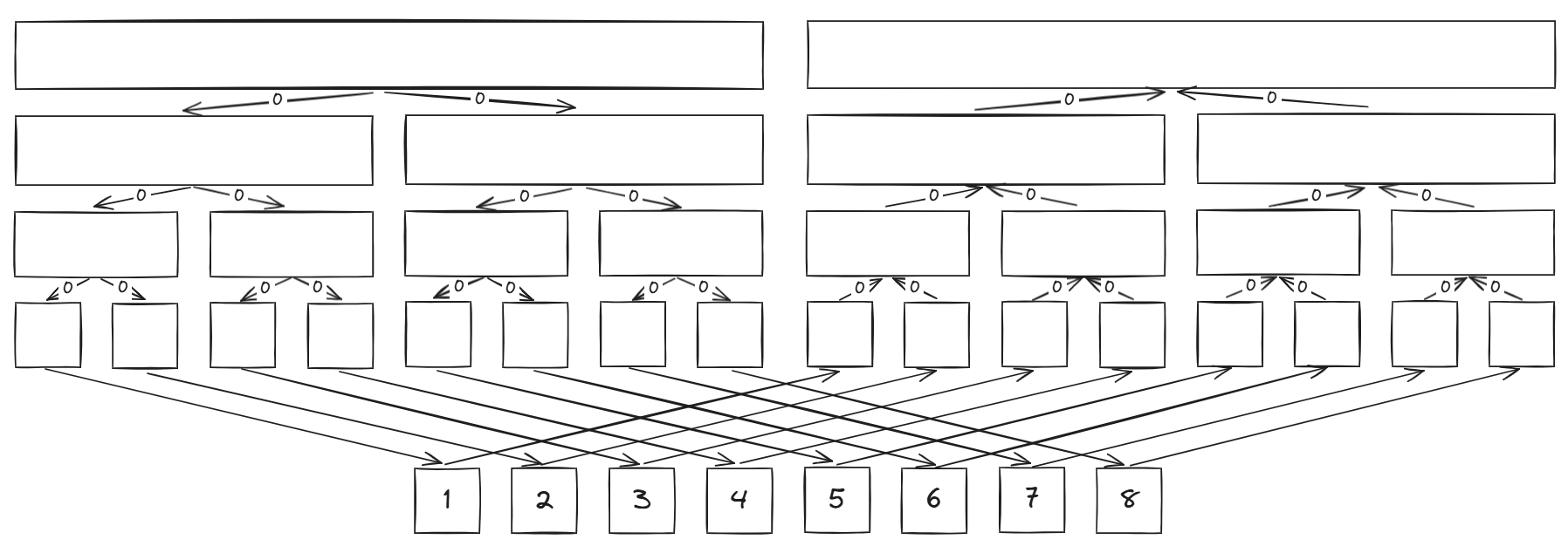
时间复杂度
代码
#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;
using ll = long long;
const int MAXN = 100001;
const ll INF = (ll)(1e18);
struct Node {
int u;
ll dis;
};
struct cmp {
bool operator()(const Node &a, const Node &b) const {
return a.dis > b.dis;
}
};
vector<pii> e[10 * MAXN];
struct Segment_Tree {
int l[4 * MAXN], r[4 * MAXN], id[4 * MAXN];
void build(int u, int s, int t, int x, bool op) {
l[u] = s, r[u] = t, id[u] = u + x;
if(s == t) {
(!op ? e[id[u]].push_back({s, 0}) : e[s].push_back({id[u], 0}));
return;
}
int mid = (s + t) >> 1;
build(2 * u, s, mid, x, op), build(2 * u + 1, mid + 1, t, x, op);
(!op ? (e[id[u]].push_back({id[2 * u], 0}), e[id[u]].push_back({id[2 * u + 1], 0})) : (e[id[2 * u]].push_back({id[u], 0}), e[id[2 * u + 1]].push_back({id[u], 0})));
}
void update(int u, int s, int t, int v, int w, bool op) {
if(l[u] >= s && r[u] <= t) {
(!op ? e[v].push_back({id[u], w}) : e[id[u]].push_back({v, w}));
return;
}
if(s <= r[2 * u]) {
update(2 * u, s, t, v, w, op);
}
if(t >= l[2 * u + 1]) {
update(2 * u + 1, s, t, v, w, op);
}
}
}tr[2];
int n, q, s;
bool vis[10 * MAXN];
ll dist[10 * MAXN];
void dij(int s) {
priority_queue<Node, vector<Node>, cmp> pq;
fill(dist + 1, dist + 10 * n + 1, INF);
dist[s] = 0;
pq.push({s, 0});
for(; !pq.empty(); ) {
auto [u, dis] = pq.top();
pq.pop();
if(vis[u]) {
continue;
}
vis[u] = 1;
for(auto [v, w] : e[u]) {
if(dis + w < dist[v]) {
dist[v] = dis + w;
pq.push({v, dis + w});
}
}
}
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> q >> s;
tr[0].build(1, 1, n, n, 0), tr[1].build(1, 1, n, 5 * n, 1);
for(int i = 1, op, u, v, w, l, r; i <= q; ++i) {
cin >> op;
if(op == 1) {
cin >> u >> v >> w;
e[u].push_back({v, w});
}else if(op == 2) {
cin >> u >> l >> r >> w;
tr[0].update(1, l, r, u, w, 0);
}else {
cin >> u >> l >> r >> w;
tr[1].update(1, l, r, u, w, 1);
}
}
dij(s);
for(int i = 1; i <= n; ++i) {
cout << (dist[i] == INF ? -1 : dist[i]) << " ";
}
return 0;
}
本文作者:Yaosicheng124
本文链接:https://www.cnblogs.com/yaosicheng124/p/18314339
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步