扫描线

简介

扫描线，顾名思义，就是一根线扫过去。

矩形面积并

给定平面直角坐标系上 \(N\) 个矩形，每个矩形的边均平行于 \(x\) 轴或 \(y\) 轴。求这些矩形的面积并。(被多个矩形覆盖的区域只算一遍)

首先考虑一维上的问题：有 \(N\) 条线段，求这些线段的长度并。比如下图：

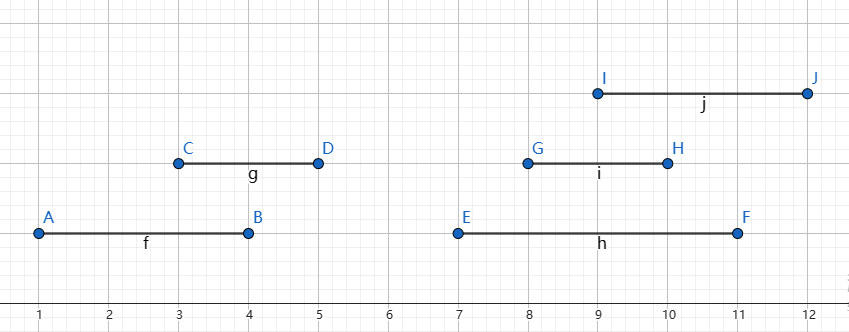
令线段左端点为 \(1\)，右端点为 \(-1\)。

现在我们再画一条垂直于 \(x\) 轴的扫描线，并让它扫过所有线段的端点：

• 当扫到 \(A\) 时，之前和都为 \(0\)，所以对答案没有贡献。
• 当扫到 \(C\) 时，之前和都为 \(1\)，所以对答案造成 \(3-1=2\) 的贡献。
• 当扫到 \(B\) 时，之前和都为 \(2\)，所以对答案造成 \(4-3=1\) 的贡献。
• 当扫到 \(D\) 时，之前和都为 \(1\)，所以对答案造成 \(5-4=1\) 的贡献。
• 当扫到 \(E\) 时，之前和都为 \(0\)，所以对答案没有贡献。
• 当扫到 \(G\) 时，之前和都为 \(1\)，所以对答案造成 \(8-7=1\) 的贡献。
• 当扫到 \(I\) 时，之前和都为 \(2\)，所以对答案造成 \(9-8=1\) 的贡献。
• 当扫到 \(H\) 时，之前和都为 \(3\)，所以对答案造成 \(10-9=1\) 的贡献。
• 当扫到 \(F\) 时，之前和都为 \(2\)，所以对答案造成 \(11-10=1\) 的贡献。
• 当扫到 \(J\) 时，之前和都为 \(2\)，所以对答案造成 \(12-11=1\) 的贡献。

这就是用扫描线解决该问题的思路。

我们可以将这些矩形看成很多条线段，就像这样：

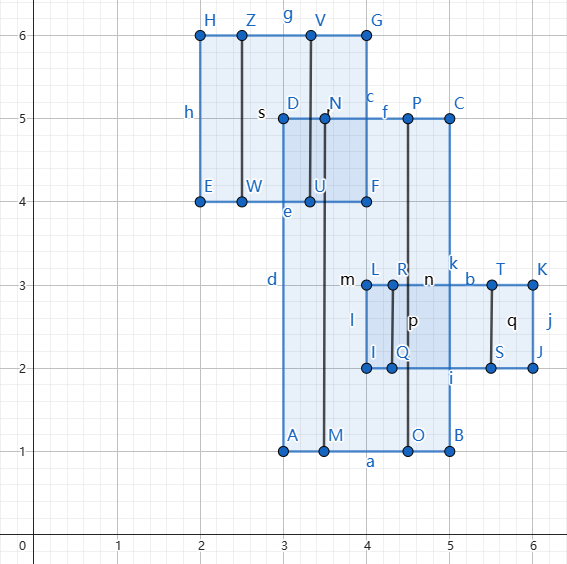
这时，我们就把二维问题转化成了许多一维问题。

而我们可以用一个线段树维护所有的和的最小值和数量，而查询非 \(0\) 值的数量可以转化为：

• 若最小值为 \(0\)，则非零元素数量为所有元素数量 \(-\) 最小值数量。
• 否则，非零元素数量为所有元素数量。

如果 \(y\) 很大，需要离散化。

时间复杂度 \(O(N\log N)\)，空间复杂度 \(O(N)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int MAXN = 200001;

struct Node {
  int x, l, r, op;
}s[MAXN];

struct INFO {
  int Min, cnt;
  INFO operator+(const INFO &a) {
    return INFO{min(Min, a.Min), (Min <= a.Min ? cnt : 0) + (a.Min <= Min ? a.cnt : 0)};
  }
  INFO operator+(const int &a) {
    return INFO{Min + a, cnt};
  }
  INFO operator+=(const INFO &a) {
    return *this = *this + a;
  }
  INFO operator+=(const int &a) {
    return *this = *this + a;
  }
};

struct Segment_Tree {
  int l[4 * MAXN], r[4 * MAXN], lazy[4 * MAXN], y[2 * MAXN];
  INFO v[4 * MAXN];
  void build(int u, int s, int t) {
    l[u] = s, r[u] = t, lazy[u] = 0;
    if(s == t) {
      v[u] = INFO{0, y[s] - y[s - 1]};
      return;
    }
    int mid = (s + t) >> 1;
    build(2 * u, s, mid), build(2 * u + 1, mid + 1, t);
    v[u] = v[2 * u] + v[2 * u + 1];
  }
  void tag(int u, int x) {
    v[u] += x, lazy[u] += x;
  }
  void pushdown(int u) {
    tag(2 * u, lazy[u]), tag(2 * u + 1, lazy[u]), lazy[u] = 0;
  }
  void update(int u, int s, int t, int x) {
    if(l[u] >= s && r[u] <= t) {
      tag(u, x);
      return;
    }
    pushdown(u);
    if(s <= r[2 * u]) {
      update(2 * u, s, t, x);
    }
    if(t >= l[2 * u + 1]) {
      update(2 * u + 1, s, t, x);
    }
    v[u] = v[2 * u] + v[2 * u + 1];
  }
  INFO GetInfo(int u, int s, int t) {
    if(l[u] >= s && r[u] <= t) {
      return v[u];
    }
    pushdown(u);
    INFO x = INFO{INT_MAX, 0};
    if(s <= r[2 * u]) {
      x += GetInfo(2 * u, s, t);
    }
    if(t >= l[2 * u + 1]) {
      x += GetInfo(2 * u + 1, s, t);
    }
    return x;
  }
}tr;

int n, tot;
ll ans;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n;
  for(int i = 1, x, y, x2, y2; i <= n; ++i) {
    cin >> x >> y >> x2 >> y2;
    s[i] = {x, y, y2, 1};
    s[n + i] = {x2, y, y2, -1};
    tr.y[i] = y;
    tr.y[n + i] = y2;
  }
  sort(tr.y + 1, tr.y + 2 * n + 1);
  for(int i = 1; i <= 2 * n; ++i) {
    if(!tot || tr.y[i] > tr.y[tot]) {
      tr.y[++tot] = tr.y[i];
    }
  }
  for(int i = 1; i <= 2 * n; ++i) {
    s[i].l = lower_bound(tr.y + 1, tr.y + tot + 1, s[i].l) - tr.y;
    s[i].r = lower_bound(tr.y + 1, tr.y + tot + 1, s[i].r) - tr.y;
  }
  sort(s + 1, s + 2 * n + 1, [](const Node &a, const Node &b) { return a.x < b.x; });
  tr.build(1, 1, tot);
  for(int i = 1; i <= 2 * n; ++i) {
    INFO x = tr.GetInfo(1, 1, tot);
    ans += 1ll * (s[i].x - s[i - 1].x) * (x.Min ? tr.y[tot] : tr.y[tot] - x.cnt);
    tr.update(1, s[i].l + 1, s[i].r, s[i].op);
  }
  cout << ans;
  return 0;
}

CF 269 D

题目描述

在一面高为 \(t\) 的墙上，有 \(N\) 块水平的面板，第 \(i\) 块高度为 \(h_i\)，覆盖 \([l_i,r_i]\) 的区域。墙顶可以看作是高度为 \(t\) 的面板 \([-10^9,10^9]\)，同样，墙底可以看作高度为 \(0\) 的面板 \([-10^9,10^9]\)。

将有水从墙顶流出。水流能从 \(u\rightarrow v\) 当且仅当：

• \(h_u>h_v\)。
• \(\max(l_u,l_v)<\min(r_u,r_v)\)。
• 不存在结点 \(w(w\ne u,v)\) 使得水流能从 \(u\rightarrow w,w\rightarrow v\)。

并且 \(u\rightarrow v\) 的流量为 \(\min(r_u,r_v)-\max(l_u,l_v)\)。一条路径的流量为其路径上经过边的流量的最小值。

求从墙顶到墙底的最大流量。

思路

我们从左往右做一遍扫描线。

每次我们扫到一个面板 \(u\) 的左端点，那么我们就找到在这个面板之上和之下的第一个面板 \(v_1,v_2\)，由于有墙顶墙底的存在，所以必定能找到。然后我们建边 \(v_1\rightarrow u,u\rightarrow v_2\)，但此时 \(v_1\rightarrow v_2\) 的边就要删除。上述可以用 set，map 求解。

建完图后拓扑排序即可。

空间复杂度 \(O(N)\)，时间复杂度 \(O(N\log N)\)。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001;

struct Node {
  int x, h, op, id;
}s[MAXN];

struct LINE {
  int l, r, h;
}a[MAXN];

int n, t, in[MAXN], dp[MAXN], id[MAXN];
vector<int> e[MAXN];
map<pii, bool> mp;

void DP() {
  iota(id + 1, id + n + 3, 1);
  sort(id + 1, id + n + 3, [](const int &x, const int &y) { return a[x].h > a[y].h; });
  dp[id[1]] = int(2e9);
  for(int i = 1; i <= n + 2; ++i) {
    for(int v : e[id[i]]) {
      if(!mp.count({id[i], v})) {
        dp[v] = max(dp[v], min(dp[id[i]], min(a[id[i]].r, a[v].r) - max(a[id[i]].l, a[v].l)));
      }
    }
  }
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> t;
  for(int i = 1, h, l, r; i <= n; ++i) {
    cin >> h >> l >> r;
    l += int(1e9), r += int(1e9);
    s[i] = {l, h, 0, i};
    s[n + i] = {r, h, 1, i};
    a[i] = {l, r, h};
  }
  a[n + 1] = {0, int(2e9), 0}, a[n + 2] = {0, int(2e9), t};
  sort(s + 1, s + 2 * n + 1, [](const Node &a, const Node &b) { return a.x < b.x || (a.x == b.x && a.op > b.op); });
  set<pii> ss;
  ss.insert({0, n + 1}), ss.insert({t, n + 2}), e[n + 2].push_back(n + 1);
  for(int i = 1; i <= 2 * n; ++i) {
    if(!s[i].op) {
      auto it = ss.upper_bound({s[i].h, 0});
      mp[{it->second, prev(it)->second}] = 1;
      e[it->second].push_back(s[i].id);
      e[s[i].id].push_back(prev(it)->second);
      ss.insert({s[i].h, s[i].id});
    }else {
      ss.erase({s[i].h, s[i].id});
    }
  }
  DP();
  cout << dp[n + 1];
  return 0;
}