自动机

简介

自动机是一种通过状态之间的跳转进行计算的数学模型。

当自动机接受一个输入字符时，它使用状态转移函数，依据当前所处的状态和输入的字符跳转至下一个状态。我们常常使用有向图表示一个有限状态自动机。此时，状态在有向图上以结点形式表示；状态转移函数表示为这张图上的有向边的集合。

比如说判断一个二进制串的奇偶性，我们可以建出以下这个自动机：

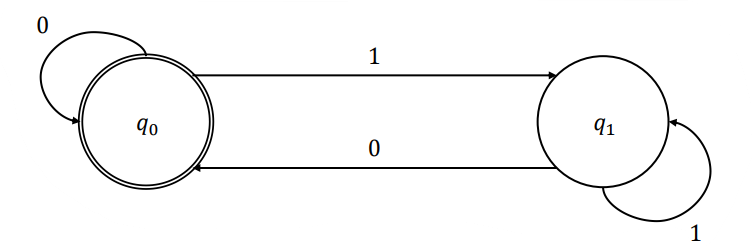
这个自动机初始状态为 \(q_0\)，如果最终状态为 \(q_0\)，则该二进制串为偶数，否则为奇数。

子序列自动机

首先考虑怎么判断一个字符串 \(T\) 是否是字符串 \(S\) 的子序列。

可以用类似于贪心的方法：令 \(q_i\) 表示当前字符串匹配到了 \(S\) 的第 \(i\) 个字符。\(q_{0}\) 为初始状态。\(q_{-1}\) 表示当前字符串不是 \(S\) 的子序列。而转移 \(\delta(q_i,c)\) 就为 \(i\) 之后第一次字符 \(c\) 的出现位置。若没有，则为 \(-1\)。

例如 \(S=abaab\) 时自动机如下：

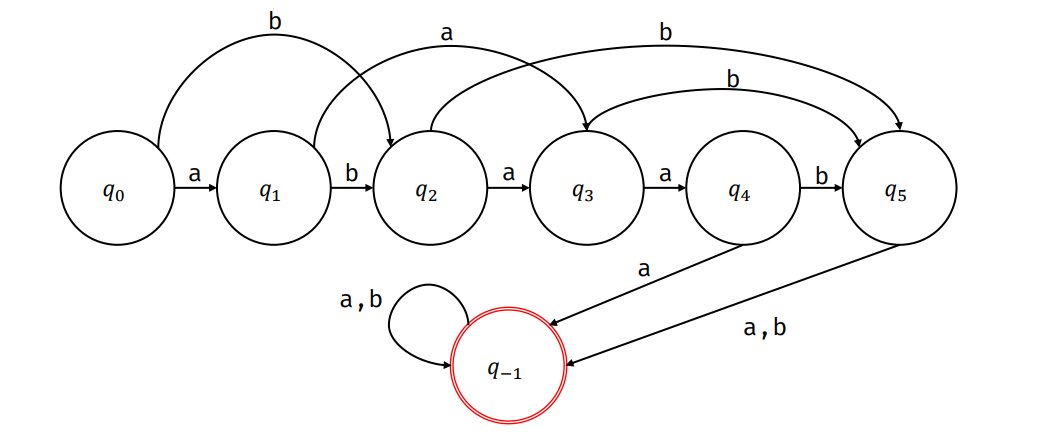
这时我们可以发现，所有在这个自动机上以 \(q_0\) 为起点，不以 \(q_{-1}\) 为终点的路径都对应着一个子序列，并且这些子序列都是本质不同的。

什么是本质不同子序列

本质不同子序列是指两个长度不等存在字符不等的子序列。即使这两个子序列在原字符串中的下标不同，只要两个字符串相等，那么它们就是本质相同的。

原因很简单：因为自动机中是取最近的一个字符，所以就不会有重复。

然后在这个自动机上做 \(dp\) 即可求出 \(S\) 的本质不同子序列数量。

时空复杂度均为 \(O(N\cdot |\sum|)\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 100005, MOD = int(1e9) + 7;

int t, n, dp[MAXN], ans, r[MAXN][26];
string s;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> s;
  n = s.size(), s = ' ' + s;
  fill(&r[n + 1][0], &r[n + 1][26], n + 1);
  for(int i = n; i >= 0; --i) {
    dp[i] = 0;
    for(int j = 0; j < 26; ++j) {
      r[i][j] = r[i + 1][j];
    }
    if(i < n) {
      r[i][s[i + 1] - 'A'] = i + 1;
    }
  }
  dp[0] = 1, ans = 0;
  for(int i = 0; i <= n; ++i) {
    for(int j = 0; j < 26; ++j) {
      dp[r[i][j]] = (dp[r[i][j]] + dp[i]) % MOD;
    }
    ans = (ans + dp[i]) % MOD;
  }
  cout << ans << "\n";
  return 0;
}

KMP 与前缀自动机

KMP

给定字符串 \(S\)，定义 \(P_i\) 表示 \(S\) 长度为 \(i\) 的前缀的 border (最长真前缀等于真后缀) 的长度。

例如 \(S=aabaaab\) 时，\(P=[0, 1, 0, 1, 2, 2, 3]\)。

假设我们已经知道了 \(P_1,P_2,\dots,P_{i-1}\)，如何求出 \(P_i\) 呢？

这张图中红色部分是前缀 \(i-1\)，绿色部分是 \(P_{i-1}\)，蓝色部分是 \(P_{P_{i-1}}\)。如果这时 \(S_{P_{i-1}+1}=S_{i}\)，则 \(P_{i}\) 为 \(P_{i-1}+1\)。否则再判断 \(P_{P_{i-1}}\)，直到找到相等的位置即可。

时空复杂度均为 \(O(N)\)。

前缀自动机

记模式串 \(S\) 的长度为 \(n\)，构造一个包含 \(q_0, q_1, \dots, q_n\) 共计 \(n + 1\)
个状态的自动机，状态 \(q_i\) 对应匹配至模式串 \(T\) 的第 \(i\) 个字符。

很容易得到以下转移：\(\delta(q_i,c)=\begin{cases}q_{i+1}&i<n\wedge S_{i+1}=c\\\delta(q_{P_i},c)&\text{otherwise}\end{cases}\)。

例如当 \(S=abaab\) 时自动机如下：

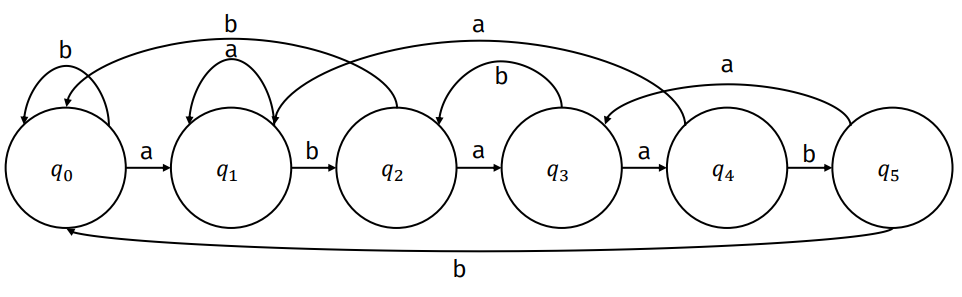
也可以通过前缀自动机反推 \(P_i\)。

时空复杂度均为 \(O(N\cdot |\sum|)\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 1000015;

int n, p[MAXN], nxt[MAXN][26];
string s;

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> s >> q;
  n = s.size(), s = ' ' + s + ' ';
  nxt[0][s[1] - 'a'] = 1;
  for(int i = 1; i < n; ++i) {
    for(int j = 0; j < 26; ++j) {
      if(i < n && j == s[i + 1] - 'a') {
        nxt[i][j] = i + 1, p[i + 1] = nxt[p[i]][j];
      }else {
        nxt[i][j] = nxt[p[i]][j];
      }
    }
  }
  for(int i = 1; i <= n; ++i) {
    cout << p[i] << " ";
  }
  return 0;
}