二分图最大匹配

简介

二分图最大匹配是这样一个问题：给定图 \(G=(V,E)\)，存在点集 \(V_1,V_2\) 满足：\(V_1 \bigcap V_2 = \emptyset 且 V_1 \bigcup V_2=V 且\neg \exists u,v \in V_1 使 (u,v)\in E 且 \neg \exists u,v \in V_2 使 (u,v)\in E\) （即是二分图）。求至多能选出多少条边的边集 \(E' \in E\) 使得 \(\forall (u_1,v_1),(u_2,v_2)\in E' 且 (u_1,v_1)\ne(u_2,v_2) 使 u_1,v_1,u_2,v_2 互不相同\)。

这里将介绍两种做法。

匈牙利算法

匈牙利算法的流程大致如下：对于每个 \(\in V_1\) 的点 \(u\)，看是否存在与其相邻的结点 \(v\) 未被选过，若有，则直接选择这条边，否则，看 \(v\) 原来连接的点能不能换一个点连接，这样不断递归下去。

实际上就是在找增广路径。

增广路径是什么？

增广路径就是类似于下面这个：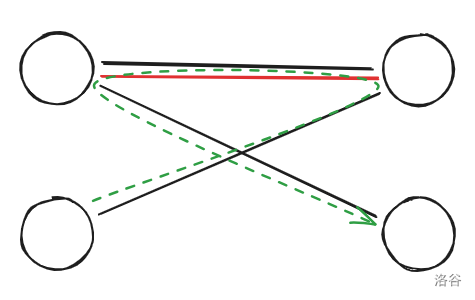

也就是头和尾都是未匹配且长度为偶数的路径。这样的路径就能增加匹配数。

由于每个点最坏要把整张图遍历一遍，所以时间复杂度 \(O(N(N+M))\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 501;

int n, m, k, pl[MAXN], pr[MAXN], ans;
bool vis[MAXN];
vector<int> e[MAXN];

bool dfs(int u) {
  if(vis[u]) {
    return 0;
  }
  vis[u] = 1;
  for(int v : e[u]) {
    if(!pr[v] || dfs(pr[v])) {
      pl[u] = v, pr[v] = u;
      return 1;
    }
  }
  return 0;
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m >> k;
  for(int i = 1, u, v; i <= k; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
  }
  for(int i = 1; i <= n; ++i) {
    fill(vis + 1, vis + n + 1, 0);
    ans += dfs(i);
  }
  cout << ans << "\n";
  for(int i = 1; i <= n; ++i) {
    if(pl[i]) {
      cout << i << " " << pl[i] << "\n";
    }
  }
  return 0;
}

Hopcroft-Karp 算法

这个算法是匈牙利算法的优化版本。

Hopcroft-Karp 算法的核心就是每次只找出最短的增广路径。这样就能使时间复杂度变为 \(O(M\sqrt N)\)。

代码

#include<bits/stdc++.h>
using namespace std;

const int MAXN = 100001;

int n, m, k, pl[MAXN], pr[MAXN], ans, dis[MAXN];
bool vis[MAXN];
vector<int> e[MAXN];

bool dfs(int u) {
  if(vis[u]) {
    return 0;
  }
  vis[u] = 1;
  for(int v : e[u]) {
    if(!pr[v] || (dis[pr[v]] == dis[u] + 1 && dfs(pr[v]))) {
      pl[u] = v, pr[v] = u;
      return 1;
    }
  }
  return 0;
}

bool bfs() {
  fill(vis + 1, vis + n + 1, 0);
  fill(dis + 1, dis + n + 1, 0);
  queue<int> que;
  for(int i = 1; i <= n; ++i) {
    if(!pl[i]) {
      que.push(i), dis[i] = 1;
    }
  }
  for(; !que.empty(); ) {
    int u = que.front();
    que.pop();
    for(int v : e[u]) {
      if(!pr[v]) {
        return 1;
      }
      if(!dis[pr[v]]) {
        dis[pr[v]] = dis[u] + 1, que.push(pr[v]);
      }
    }
  }
  return 0;
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m >> k;
  for(int i = 1, u, v; i <= k; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
  }
  while(bfs()) {
    for(int i = 1; i <= n; ++i) {
      ans += (!pl[i] && dfs(i));
    }
  }
  cout << ans << "\n";
  for(int i = 1; i <= n; ++i) {
    if(pl[i]) {
      cout << i << " " << pl[i] << "\n";
    }
  }
  return 0;
}

最小点覆盖

最小点覆盖是这一类问题：给定一个二分连通图，求最少要选择多少个点才能使得所有点至少有一个相邻点或自己被选中？

这个问题实际上等价于最大匹配，因为若有某个点不满足这个条件，则代表其所有相邻点均未被选中，即仍有增广路径。所以最小点覆盖和最大图匹配均 \(+1\)，即 最小点覆盖 \(=\) 最大图匹配。

但要怎么构造方案呢？

依次看每条匹配的边，

最大独立集

最大独立集是指在一个二分图上选出最多的点，使得所有的点均没有共同相邻点。这个东西也可以转化为最小点覆盖，因为最大独立集和最小点覆盖是相反的，即 最大独立集 \(=N-\) 最小点覆盖 \(=N-\) 最大图匹配。

最小路径覆盖

给定一张图，求最少需要使用多少条互不相交的简单路径使得所有点恰好被一条路径包含？

一开始我们先让每条路径只有一个点，比如下图：

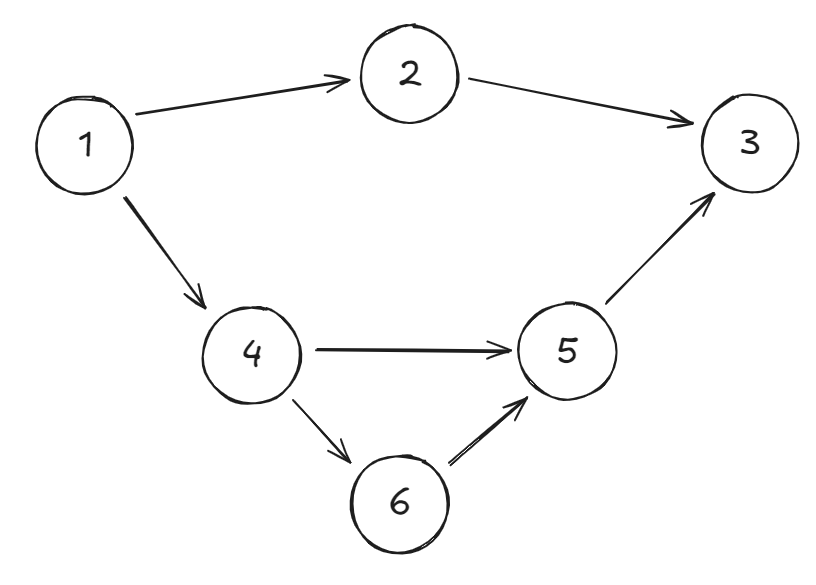
接着考虑不断选择边来合并路径。

但不能随便合并，需要满足每个结点的入度和出度不超过 \(1\)。

很容易想到将每个点拆成入和出两个点，接着跑二分图最大匹配。。

答案就为 $N - $ 二分图最大匹配。

代码

#include<bits/stdc++.h>
using namespace std;
using pii = pair<int, int>;

const int MAXN = 200001;

int n, m, k, pl[MAXN], pr[MAXN], ans, dis[MAXN];
bool vis[MAXN];
vector<int> e[MAXN];
map<pii, int> pos;

bool dfs(int u) {
  if(vis[u]) {
    return 0;
  }
  vis[u] = 1;
  for(int v : e[u]) {
    if(!pr[v] || (dis[pr[v]] == dis[u] + 1 && dfs(pr[v]))) {
      pl[u] = v, pr[v] = u;
      return 1;
    }
  }
  return 0;
}

bool bfs() {
  fill(vis + 1, vis + n + 1, 0);
  fill(dis + 1, dis + n + 1, 0);
  queue<int> que;
  for(int i = 1; i <= n; ++i) {
    if(!pl[i]) {
      que.push(i), dis[i] = 1;
    }
  }
  for(; !que.empty(); ) {
    int u = que.front();
    que.pop();
    for(int v : e[u]) {
      if(!pr[v]) {
        return 1;
      }
      if(!dis[pr[v]]) {
        dis[pr[v]] = dis[u] + 1, que.push(pr[v]);
      }
    }
  }
  return 0;
}

int main() {
  ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
  cin >> n >> m;
  for(int i = 1, u, v; i <= m; ++i) {
    cin >> u >> v;
    e[u].push_back(v);
  }
  ans = 0;
  while(bfs()) {
    for(int i = 1; i <= n; ++i) {
      ans += (!pl[i] && dfs(i));
    }
  }
  for(int i = 1; i <= n; ++i) {
    if(!pr[i]) {
      for(int j = i; j; j = pl[j]) {
        cout << j << " ";
      }
      cout << "\n";
    }
  }
  cout << n - ans;
  return 0;
}